Пример решения прямой и двойственной задачи симплекс методом

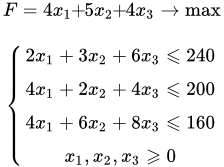
Условие задачи, решаемой симплекс-методом.

Рассмотрен пример решения задачи симплекс методом, а также пример решения двойственной задачи.

Содержание

Условие задачи

Для реализации трех групп товаров коммерческое предприятие располагает тремя видами ограниченных материально-денежных ресурсов в количестве b₁ = 240, b₂ = 200, b₃ = 160 единиц. При этом для продажи 1 группы товаров на 1 тыс. руб. товарооборота расходуется ресурса первого вида в количестве a₁₁ = 2 единицы, ресурса второго вида в количестве a₂₁ = 4 единицы, ресурса третьего вида в количестве a₃₁ = 4 единицы. Для продажи 2 и 3 групп товаров на 1 тыс. руб. товарооборота расходуется соответственно ресурса первого вида в количестве a₁₂ = 3, a₁₃ = 6 единицы, ресурса второго вида в количестве a₂₂ = 2, a₂₃ = 4 единицы, ресурса третьего вида в количестве a₃₂ = 6, a₃₃ = 8 единиц. Прибыль от продажи трех групп товаров на 1 тыс. руб. товарооборота составляет соответственно c₁ = 4, c₂ = 5, c₃ = 4 (тыс. руб.). Определить плановый объем и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной.

К прямой задаче планирования товарооборота, решаемой симплекс методом, составить двойственную задачу линейного программирования.
Установить сопряженные пары переменных прямой и двойственной задачи.
Согласно сопряженным парам переменных из решения прямой задачи получить решение двойственной задачи, в которой производится оценка ресурсов, затраченных на продажу товаров.

Решение задачи симплекс методом

Пусть x₁, x₂, x₃ - количество реализованных товаров, в тыс. руб., 1, 2, 3 - ей групп, соответственно. Тогда математическая модель задачи имеет вид.

F = 4·x₁ + 5·x₂ + 4·x₃ –>max

Решаем симплекс методом.
Вводим дополнительные переменные x₄ ≥ 0, x₅ ≥ 0, x₆ ≥ 0, чтобы неравенства преобразовать в равенства.

В качестве базиса возьмем x₄ = 240; x₅ = 200; x₆ = 160.
Данные заносим в симплекс таблицу

Симплекс таблица № 1

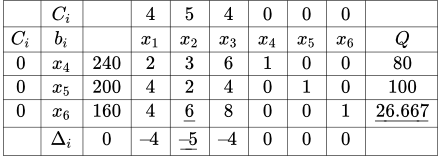
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline&C_i & & 4 & 5 & 4 & 0 & 0 & 0\\ \hline C_i&b_i & &x_1&x_2&x_3&x_4&x_5&x_6&Q\\ \hline 0 & x_4 & 240 & 2&3 & 6 & 1 & 0 & 0&80 \\ \hline0 & x_5 & 200 & 4&2 & 4 & 0 & 1 & 0&100 \\ \hline0 & x_6 & 160 & 4&\underline{6} & 8 & 0 & 0 & 1&\underline{26.667} \\ \hline & \Delta_i &0&{ \kern-0.2em-\kern-0.2em 4}&\underline{{ \kern-0.2em-\kern-0.2em 5}}&{ \kern-0.2em-\kern-0.2em 4}&0&0&0&\\ \hline\end{array}$

Целевая функция:

Вычисляем оценки по формуле:
.

Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:
Δ₂ = – 5

Вводим переменную x₂ в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение для столбца x₂:

= 26.667
Наименьшее неотрицательное: Q₃ = 26.667. Выводим переменную x₆ из базиса.
3-ю строку делим на 6.
Из 1-й строки вычитаем 3-ю строку, умноженную на 3
Из 2-й строки вычитаем 3-ю строку, умноженную на 2
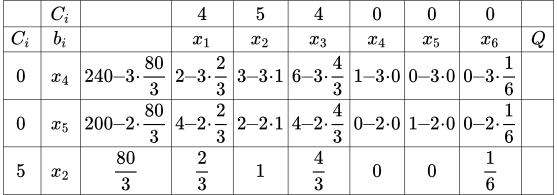
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline&C_i & & 4 & 5 & 4 & 0 & 0 & 0\\ \hline C_i&b_i & &x_1&x_2&x_3&x_4&x_5&x_6&Q\\ \hline 0 & x_4 & \kern-0.3em 240\kern-0.3em-\kern-0.3em 3\kern-0.2em\cdot\kern-0.2em \frac{80}{3}\kern-0.3em & \kern-0.3em 2\kern-0.3em-\kern-0.3em 3\kern-0.2em\cdot\kern-0.2em \frac{2}{3}\kern-0.3em & \kern-0.3em 3\kern-0.3em-\kern-0.3em 3\kern-0.2em\cdot\kern-0.2em 1\kern-0.3em & \kern-0.3em 6\kern-0.3em-\kern-0.3em 3\kern-0.2em\cdot\kern-0.2em \frac{4}{3}\kern-0.3em & \kern-0.3em 1\kern-0.3em-\kern-0.3em 3\kern-0.2em\cdot\kern-0.2em 0\kern-0.3em & \kern-0.3em 0\kern-0.3em-\kern-0.3em 3\kern-0.2em\cdot\kern-0.2em 0\kern-0.3em & \kern-0.3em 0\kern-0.3em-\kern-0.3em 3\kern-0.2em\cdot\kern-0.2em \frac{1}{6}\kern-0.3em & \\ \hline0 & x_5 & \kern-0.3em 200\kern-0.3em-\kern-0.3em 2\kern-0.2em\cdot\kern-0.2em \frac{80}{3}\kern-0.3em & \kern-0.3em 4\kern-0.3em-\kern-0.3em 2\kern-0.2em\cdot\kern-0.2em \frac{2}{3}\kern-0.3em & \kern-0.3em 2\kern-0.3em-\kern-0.3em 2\kern-0.2em\cdot\kern-0.2em 1\kern-0.3em & \kern-0.3em 4\kern-0.3em-\kern-0.3em 2\kern-0.2em\cdot\kern-0.2em \frac{4}{3}\kern-0.3em & \kern-0.3em 0\kern-0.3em-\kern-0.3em 2\kern-0.2em\cdot\kern-0.2em 0\kern-0.3em & \kern-0.3em 1\kern-0.3em-\kern-0.3em 2\kern-0.2em\cdot\kern-0.2em 0\kern-0.3em & \kern-0.3em 0\kern-0.3em-\kern-0.3em 2\kern-0.2em\cdot\kern-0.2em \frac{1}{6}\kern-0.3em & \\ \hline5 & x_2 & \frac{80}{3} & \frac{2}{3} & 1 & \frac{4}{3} & 0 & 0 & \frac{1}{6}& \\ \hline\end{array}$

Вычисляем:

Получаем новую таблицу.

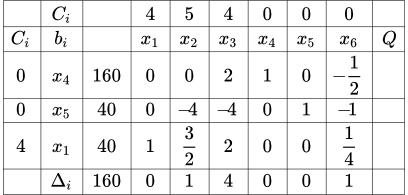
Симплекс таблица № 2

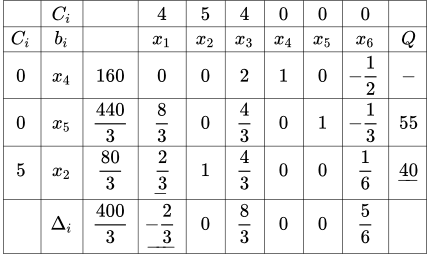
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline&C_i & & 4 & 5 & 4 & 0 & 0 & 0\\ \hline C_i&b_i & &x_1&x_2&x_3&x_4&x_5&x_6&Q\\ \hline 0 & x_4 & 160&0 & 0 & 2 & 1 & 0 & { \kern-0.2em-\kern-0.2em \frac{1}{2}}&- \\ \hline0 & x_5 & \frac{440}{3}&\frac{8}{3} & 0 & \frac{4}{3} & 0 & 1 & { \kern-0.2em-\kern-0.2em \frac{1}{3}}&55 \\ \hline5 & x_2 & \frac{80}{3}&\underline{\frac{2}{3}} & 1 & \frac{4}{3} & 0 & 0 & \frac{1}{6}&\underline{40} \\ \hline & \Delta_i &\frac{400}{3}&\underline{{ \kern-0.2em-\kern-0.2em \frac{2}{3}}}&0&\frac{8}{3}&0&0&\frac{5}{6}&\\ \hline\end{array}$

Целевая функция:

Вычисляем оценки по формуле:
.

Поскольку есть отрицательная оценка Δ₁ = – 2/3, то план не оптимален.

Вводим переменную x₁ в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение для столбца x₁:

Наименьшее неотрицательное: Q₃ = 40. Выводим переменную x₂ из базиса.
3-ю строку делим на 2/3.
Из 2-й строки вычитаем 3-ю строку, умноженную на 8/3
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline&C_i & & 4 & 5 & 4 & 0 & 0 & 0\\ \hline C_i&b_i & &x_1&x_2&x_3&x_4&x_5&x_6&Q\\ \hline 0 & x_4 & 160 & 0 & 0 & 2 & 1 & 0 & { \kern-0.2em-\kern-0.2em \frac{1}{2}}& \\ \hline0 & x_5 & \kern-0.3em \frac{440}{3}\kern-0.3em-\kern-0.3em \frac{8}{3}\kern-0.2em\cdot\kern-0.2em 40\kern-0.3em & \kern-0.3em \frac{8}{3}\kern-0.3em-\kern-0.3em \frac{8}{3}\kern-0.2em\cdot\kern-0.2em 1\kern-0.3em & \kern-0.3em 0\kern-0.3em-\kern-0.3em \frac{8}{3}\kern-0.2em\cdot\kern-0.2em \frac{3}{2}\kern-0.3em & \kern-0.3em \frac{4}{3}\kern-0.3em-\kern-0.3em \frac{8}{3}\kern-0.2em\cdot\kern-0.2em 2\kern-0.3em & \kern-0.3em 0\kern-0.3em-\kern-0.3em \frac{8}{3}\kern-0.2em\cdot\kern-0.2em 0\kern-0.3em & \kern-0.3em 1\kern-0.3em-\kern-0.3em \frac{8}{3}\kern-0.2em\cdot\kern-0.2em 0\kern-0.3em & \kern-0.3em { \kern-0.2em-\kern-0.2em \frac{1}{3}}\kern-0.3em-\kern-0.3em \frac{8}{3}\kern-0.2em\cdot\kern-0.2em \frac{1}{4}\kern-0.3em & \\ \hline4 & x_1 & 40 & 1 & \frac{3}{2} & 2 & 0 & 0 & \frac{1}{4}& \\ \hline\end{array}$

Вычисляем:

Получаем новую таблицу.

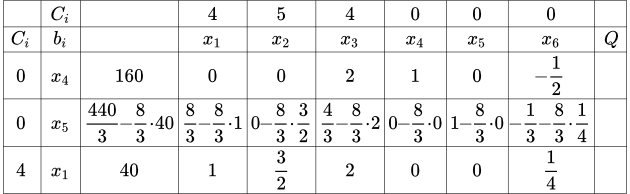
Симплекс таблица № 3

$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline&C_i & & 4 & 5 & 4 & 0 & 0 & 0\\ \hline C_i&b_i & &x_1&x_2&x_3&x_4&x_5&x_6&Q\\ \hline 0 & x_4 & 160 & 0 & 0 & 2 & 1 & 0 & { \kern-0.2em-\kern-0.2em \frac{1}{2}}& \\ \hline0 & x_5 & 40 & 0 & { \kern-0.2em-\kern-0.2em 4} & { \kern-0.2em-\kern-0.2em 4} & 0 & 1 & { \kern-0.2em-\kern-0.2em 1}& \\ \hline4 & x_1 & 40 & 1 & \frac{3}{2} & 2 & 0 & 0 & \frac{1}{4}& \\ \hline & \Delta_i &160&0&1&4&0&0&1&\\ \hline\end{array}$

Целевая функция:

Вычисляем оценки по формуле:
.

Поскольку отрицательных оценок нет, то план оптимален.

Решение задачи: x₁ = 40; x₂ = 0; x₃ = 0; x₄ = 160; x₅ = 40; x₆ = 0; F_max = 160

Ответ

x₁ = 40; x₂ = 0; x₃ = 0; x₄ = 160; x₅ = 40; x₆ = 0; F_max = 160
То есть необходимо реализовать товар первого вида в объеме 40 тыс. руб. Товар 2-го и 3-го видов реализовывать не надо. При этом максимальная прибыль составит F_max = 160 тыс. руб.

Решение двойственной задачи

Двойственная задача имеет вид:
Z = 240·y₁ + 200·y₂ + 160·y₃ –>min

Вводим дополнительные переменные y₄ ≥ 0, y₅ ≥ 0, y₆ ≥ 0, чтобы неравенства преобразовать в равенства.

Сопряженные пары переменных прямой и двойственной задач имеют вид:

Основные			Дополнительные
x₁	x₂	x₃	x₄	x₅	x₆
y₄	y₅	y₆	y₁	y₂	y₃
Дополнительные			Основные

Из последней симплекс таблицы № 3 прямой задачи, находим решение двойственной задачи:
Z_min = F_max = 160;
y₁ = Δ₄ = 0; y₂ = Δ₅ = 0; y₃ = Δ₆ = 1; y₄ = Δ₁ = 0; y₅ = Δ₂ = 1; y₆ = Δ₃ = 4;

Ответ

y₁ = 0; y₂ = 0; y₃ = 1; Z_min = 160.

Автор: Олег Одинцов. Опубликовано: 08-12-2011