Теорема о ранге матрицы системы ограничений транспортной задачи

Доказана теорема, согласно которой ранг матрицы коэффициентов системы ограничений транспортной задачи равен сумме числа поставщиков и потребителей минус один. Доказательство выполняется приведением матрицы к диагональному виду с помощью преобразований Жордана-Гаусса. Рассмотрено условие совместности системы уравнений транспортной задачи.

Содержание

См. также:

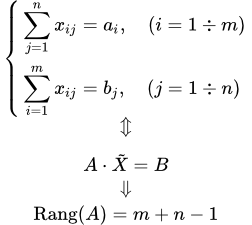
Теорема

Рассмотрим транспортную задачу.
(1)
(2)
(3)
(4) ,
(5) .

Ранг матрицы системы ограничений (2) – (3) транспортной задачи равен m + n – 1.

Доказательство

Доказательство для частного случая

Чтобы сделать доказательство более прозрачным, докажем теорему для случая с , а затем приведем доказательство для общего случая с произвольными m и n.

Запишем систему ограничений (2) – (3) в матричном виде:
.
Здесь
$A=\left(\begin{array}{c}1&1&1&0&0&0&0&0&0&0&0&0\\ 0&0&0&1&1&1&0&0&0&0&0&0\\ 0&0&0&0&0&0&1&1&1&0&0&0\\ 0&0&0&0&0&0&0&0&0&1&1&1\\ 1&0&0&1&0&0&1&0&0&1&0&0\\ 0&1&0&0&1&0&0&1&0&0&1&0\\ 0&0&1&0&0&1&0&0&1&0&0&1\end{array}\right)$ , ,

Ранг матрицы A равен числу ее линейно независимых строк или столбцов. Воспользуемся тем, что ранг не меняется при выполнении линейных преобразований Жордана-Гаусса над ее строками или столбцами. С помощью этих преобразований мы приведем матрицу к диагональному виду. Тогда ранг матрицы будет равен числу столбцов (или строк) с ненулевыми элементами по диагонали.

1.1. Из четвертого столбца матрицы A вычтем первый столбец:
.
Аналогичным образом из 5-го столбца вычтем 2-ой, из 6-го 3-ий, из 7-го 1-ый, из 8-го 2-ой, из 9-го 3-ий, из 10-го 1-ый, из 11-го 2-ой, из 12-го 3-ий. Получим матрицу , ранг которой равен рангу исходной матрицы A:
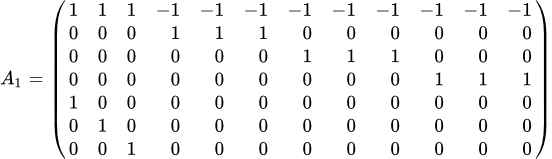
$A_1=\left(\begin{array}{r}1&1&1&-1&-1&-1&-1&-1&-1&-1&-1&-1\\ 0&0&0&1&1&1&0&0&0&0&0&0\\ 0&0&0&0&0&0&1&1&1&0&0&0\\ 0&0&0&0&0&0&0&0&0&1&1&1\\ 1&0&0&0&0&0&0&0&0&0&0&0\\ 0&1&0&0&0&0&0&0&0&0&0&0\\ 0&0&1&0&0&0&0&0&0&0&0&0\end{array}\right)$

1.2. Замечаем, что 4, 5 и 6-ой столбцы одинаковые. Мы можем вычеркнуть два из них, поскольку если вычесть один из другого, получится столбец, состоящий из одних нулей. Также одинаковыми являются 7, 8, 9-ый и 10, 11, 12-ый столбцы. Вычеркиваем лишние одинаковые столбцы. Получаем матрицу :

1.3. К первой строке прибавим 2, 3, 4-ю и вычтем 5, 6 и 7-ю строки:

1.4. Вычеркиваем первую строку с одними нулями, и переставим последние три строки в начало:

Мы получили единичную матрицу, ранг которой равен числу ее столбцов (или строк): . Тем самым мы нашли, что в этом частном случае,
.

Доказательство для общего случая

Теперь проделаем то же самое в общем случае, с произвольными m и n.

Система ограничений (2) – (3) имеет вид:
(6) ,
где
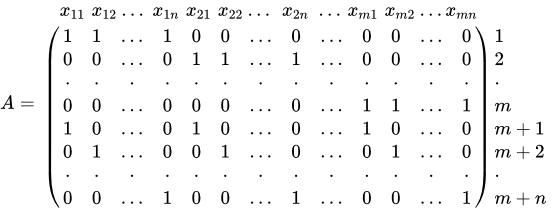$A=\begin{array}{r}x_{11}\;x_{12}\dots \;x_{1n}\;x_{21}\;x_{22}\dots \;\,x_{2n}\;\dots \,x_{m1}\;x_{m2}\dots x_{mn}\mkern3.7em\\ \left(\begin{array}{c}1&1&\dots&1&0&0&\dots&0&\dots&0&0&\dots&0\\ 0&0&\dots&0&1&1&\dots&1&\dots&0&0&\dots&0\\ \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ 0&0&\dots&0&0&0&\dots&0&\dots&1&1&\dots&1\\ 1&0&\dots&0&1&0&\dots&0&\dots&1&0&\dots&0\\ 0&1&\dots&0&0&1&\dots&0&\dots&0&1&\dots&0\\ \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ 0&0&\dots&1&0&0&\dots&1&\dots&0&0&\dots&1\end{array}\right)\begin{array}{l}1\\ 2\\ \cdot\\ m\\ m+1\\ m+2\\ \cdot\\ m+n\end{array}\end{array}$ , ,

Выполняем преобразования Жордана-Гаусса над столбцами и строками матрицы A.

2.1. Из столбцов вычитаем столбцы . Тоже самое делаем с остальными столбцами, как в пункте 1.1. ⇑ Получаем матрицу с нулями в правой нижней части:
$A_1=\left(\begin{array}{r}1&1&\dots&1&-1&-1&\dots&-1&\dots&-1&-1&\dots&-1\\ 0&0&\dots&0&1&1&\dots&1&\dots&0&0&\dots&0\\ \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ 0&0&\dots&0&0&0&\dots&0&\dots&1&1&\dots&1\\ 1&0&\dots&0&0&0&\dots&0&\dots&0&0&\dots&0\\ 0&1&\dots&0&0&0&\dots&0&\dots&0&0&\dots&0\\ \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ 0&0&\dots&1&0&0&\dots&0&\dots&0&0&\dots&0\end{array}\right)\begin{array}{l}1\\ 2\\ \cdot\\ m\\ m+1\\ m+2\\ \cdot\\ m+n\end{array}$

2.2. Вычеркиваем одинаковые столбцы:
$A_2=\left(\begin{array}{r}1&1&\dots&1&-1&-1&\dots&-1\\ 0&0&\dots&0&1&0&\dots&0\\ 0&0&\dots&0&0&1&\dots&0\\ \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ 0&0&\dots&0&0&0&\dots&1\\ 1&0&\dots&0&0&0&\dots&0\\ 0&1&\dots&0&0&0&\dots&0\\ \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ 0&0&\dots&1&0&0&\dots&0\end{array}\right)\begin{array}{l}1\\ 2\\ 3\\ \cdot\\ m\\ m+1\\ m+2\\ \cdot\\ m+n\end{array}$

2.3. К первой строке прибавим -ю строки и вычтем -ю строки:
$A_3=\left(\begin{array}{r}0&0&\dots&0&0&0&\dots&0\\ 0&0&\dots&0&1&0&\dots&0\\ 0&0&\dots&0&0&1&\dots&0\\ \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ 0&0&\dots&0&0&0&\dots&1\\ 1&0&\dots&0&0&0&\dots&0\\ 0&1&\dots&0&0&0&\dots&0\\ \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ 0&0&\dots&1&0&0&\dots&0\end{array}\right)\begin{array}{l}1\\ 2\\ 3\\ \cdot\\ m\\ m+1\\ m+2\\ \cdot\\ m+n\end{array}$

2.4. Мы получили матрицу , в которой первая строка состоит из нулей. За ней идут строк, содержащих единичную матрицу в правой части. Далее следуют строк с единичной матрицей в левой части. Вычеркиваем первую строку с одними нулями, и переставим последние строк в начало:
$A_4=\left(\begin{array}{r}1&0&\dots&0&0&0&\dots&0\\ 0&1&\dots&0&0&0&\dots&0\\ \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ 0&0&\dots&1&0&0&\dots&0\\ 0&0&\dots&0&1&0&\dots&0\\ 0&0&\dots&0&0&1&\dots&0\\ \cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot&\cdot\\ 0&0&\dots&0&0&0&\dots&1\end{array}\right)\begin{array}{l}1\\ 2\\ \cdot\\ n\\ n+1\\ n+2\\ \cdot\\ m+n-1\end{array}$
В результате мы получили единичную матрицу, число строк и столбцов которой равно m + n – 1. Ее ранг равен числу ее строк (столбцов):
.

Теорема доказана.

Существование решения

Система ограничений (2) – (3) транспортной задачи совместна тогда и только тогда, когда
сумма мощностей поставщиков равна сумме мощностей потребителей:

Поскольку ранг матрицы A системы (6), , меньше числа ее строк , то система уравнений может не иметь решений. То есть она может быть несовместной. Для того, чтобы система была совместной, необходимо и достаточно, чтобы выполнялось условие теоремы Кронекера-Капелли. Согласно этой теореме, система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы: . Напомним, что расширенная матрица системы уравнений (6) – это матрица , состоящая из столбцов матрицы и столбца свободных членов .

Исследуем вопрос о совместности системы ограничений транспортной задачи. Снова рассмотри частный случай . Расширенная матрица системы (6), в этом случае, имеет вид:
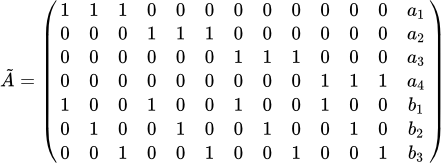
$\tilde A=\left(\begin{array}{c}1&1&1&0&0&0&0&0&0&0&0&0&a_1\\ 0&0&0&1&1&1&0&0&0&0&0&0&a_2\\ 0&0&0&0&0&0&1&1&1&0&0&0&a_3\\ 0&0&0&0&0&0&0&0&0&1&1&1&a_4\\ 1&0&0&1&0&0&1&0&0&1&0&0&b_1\\ 0&1&0&0&1&0&0&1&0&0&1&0&b_2\\ 0&0&1&0&0&1&0&0&1&0&0&1&b_3\end{array}\right)$

Выполняем те же линейные преобразования, что и при определении ранга матрицы ⇑. При этом в пунктах 1.1. и 1.2. мы выполняли действия только над столбцами матрицы . Поэтому они не затрагивают столбец свободных членов . В результате, после выполнения пункта 1.2. получаем матрицу , ранг которой равен рангу расширенной матрицы :

Далее к первой строке прибавим 2, 3, 4-ю и вычтем 5, 6 и 7-ю строки:
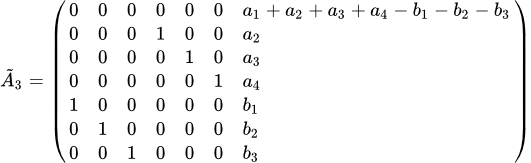
$\tilde A_3=\left(\begin{array}{l}0&0&0&0&0&0&a_1+a_2+a_3+a_4-b_1-b_2-b_3\\ 0&0&0&1&0&0&a_2\\ 0&0&0&0&1&0&a_3\\ 0&0&0&0&0&1&a_4\\ 1&0&0&0&0&0&b_1\\ 0&1&0&0&0&0&b_2\\ 0&0&1&0&0&0&b_3\end{array}\right)$
Отсюда видно, что для того, чтобы первая строка состояла только из нулей, необходимо, чтобы и в ее последнем элементе был нуль:
.
При выполнении этого условия первую строку можно вычеркнуть. Тогда ранг расширенной матрицы будет равен рангу матрицы коэффициентов :
.

Все это естественным образом переносится на общий случай произвольных m и n. При выполнении пункта 2.3. ⇑ мы должны положить:
.
Тогда первая строка будет состоять из одних нулей, и ее можно вычеркнуть. В результате получится матрица , состоящая из линейно независимых строк. Ее ранг равен . То есть ранг расширенной матрицы равен рангу матрицы системы. Тогда, согласно теореме Кронекера-Капелли, система уравнений (6) будет совместной и, следовательно, будет иметь решения. Таким образом, мы получили исходное утверждение.

Использованная литература:
Общий курс высшей математики для экономистов. Под общей редакцией В. И. Ермакова. Москва, «ИНФРА-М», 2007.

Автор: Олег Одинцов. Опубликовано: 13-09-2021

См. также: