Теоретическая механика
Описания и картинки страниц раздела «Теоретическая механика» сайта 1cov-edu.ru. Страницы содержат как теоретический материал, так и разобранные примеры решений задач.
Содержание
См. также:
Кинематика
Кинематика. Все определения, понятия, законы и теоремы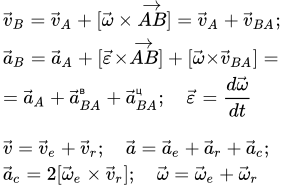 Все определения, понятия, законы и теоремы кинематики в одной странице. Материал делится на четыре основных раздела: кинематика точки, кинематика твердого тела, кинематика сложного движения точки и кинематика сложного движения твердого тела. Все картинки раздела «Кинематика»
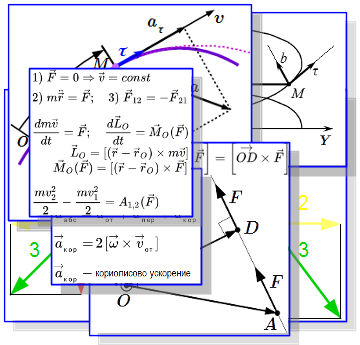
Все определения, понятия, законы и теоремы кинематики в одной странице. Материал делится на четыре основных раздела: кинематика точки, кинематика твердого тела, кинематика сложного движения точки и кинематика сложного движения твердого тела. Все картинки раздела «Кинематика»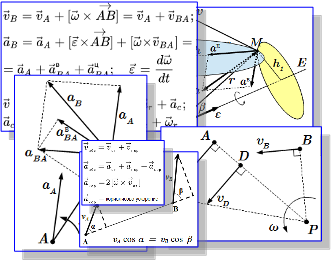 Здесь собраны все изображения раздела «Кинематика» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Что такое радиус-вектор, и чем он отличается от других векторов
Здесь собраны все изображения раздела «Кинематика» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Что такое радиус-вектор, и чем он отличается от других векторов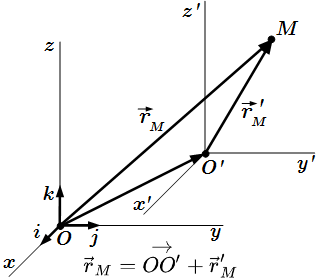 Понятие радиус-вектора и его свойства. На примерах разобрано его отличие от других векторов. Кинематика материальной точки
Понятие радиус-вектора и его свойства. На примерах разобрано его отличие от других векторов. Кинематика материальной точки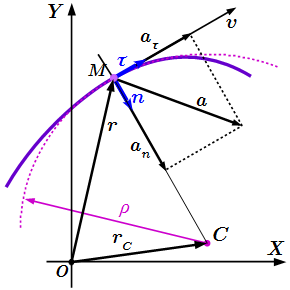 Даны основные формулы кинематики материальной точки, их вывод и изложение теории. Координатный способ задания движения точки
Даны основные формулы кинематики материальной точки, их вывод и изложение теории. Координатный способ задания движения точки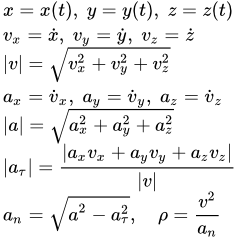 Формулы для вычисления скорости точки, ускорения, радиуса кривизны траектории, касательной, нормали и бинормали по заданным зависимостям координат от времени. Пример решения задачи, в которой по заданным уравнениям движения нужно определить скорость и ускорение точки. Также определяется радиус кривизны траектории, касательная, нормаль и бинормаль. Векторный способ задания движения точки
Формулы для вычисления скорости точки, ускорения, радиуса кривизны траектории, касательной, нормали и бинормали по заданным зависимостям координат от времени. Пример решения задачи, в которой по заданным уравнениям движения нужно определить скорость и ускорение точки. Также определяется радиус кривизны траектории, касательная, нормаль и бинормаль. Векторный способ задания движения точки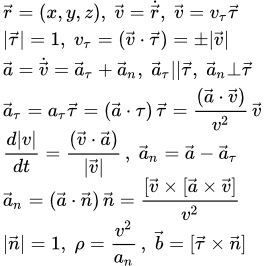 Связь векторного способа задания движения точки с координатным. Формулы для вычисления скорости точки, ускорения, радиуса кривизны траектории, касательной, нормали и бинормали при векторном способе задания движения точки. Оси естественного трехгранника Френе
Связь векторного способа задания движения точки с координатным. Формулы для вычисления скорости точки, ускорения, радиуса кривизны траектории, касательной, нормали и бинормали при векторном способе задания движения точки. Оси естественного трехгранника Френе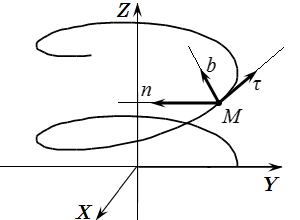 Определение естественного трехгранника Френе. Проекции скорости и ускорения точки на его оси. Пример определения ортов естественного трехгранника. Естественный способ задания движения точки
Определение естественного трехгранника Френе. Проекции скорости и ускорения точки на его оси. Пример определения ортов естественного трехгранника. Естественный способ задания движения точки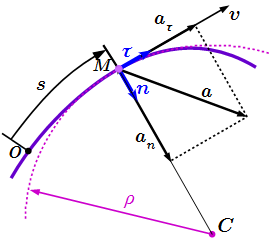 Естественный способ задания движения точки – определение и основные формулы. Пример решения задачи. Теорема о проекциях скоростей двух точек твердого тела на прямую
Естественный способ задания движения точки – определение и основные формулы. Пример решения задачи. Теорема о проекциях скоростей двух точек твердого тела на прямую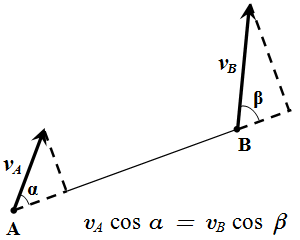 Теорема о проекциях скоростей двух точек твердого тела на прямую. Доказательство теоремы. Пример решения задачи. Скорость и ускорение точек твердого тела, совершающего поступательное и вращательное движения
Теорема о проекциях скоростей двух точек твердого тела на прямую. Доказательство теоремы. Пример решения задачи. Скорость и ускорение точек твердого тела, совершающего поступательное и вращательное движения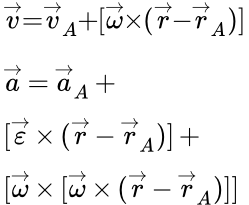 Формулы скорости (ускорения) точек твердого тела, выраженные через скорость (ускорение) полюса и угловую скорость (ускорение). Вывод этих формул из принципа, что расстояния между любыми точками тела, при его движении, остаются постоянными. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи
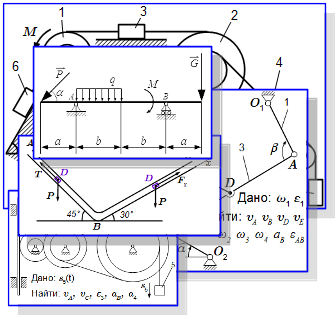
Формулы скорости (ускорения) точек твердого тела, выраженные через скорость (ускорение) полюса и угловую скорость (ускорение). Вывод этих формул из принципа, что расстояния между любыми точками тела, при его движении, остаются постоянными. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи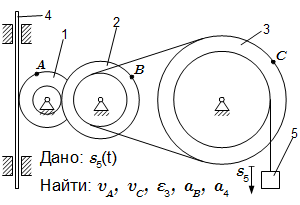 Приводятся основные законы и формулы, применяемые при решении задач на определение скоростей и ускорений точек твердого тела при вращательном движении вокруг неподвижной оси. Рассмотрен пример подробного решения задачи. В ней дан механизм, состоящий из колес, рейки и груза, соединенных нитями и зубчатой передачей. Требуется найти скорости и ускорения точек, принадлежащих звеньям этого механизма. Кинематический анализ плоского механизма – пример решения задачи
Приводятся основные законы и формулы, применяемые при решении задач на определение скоростей и ускорений точек твердого тела при вращательном движении вокруг неподвижной оси. Рассмотрен пример подробного решения задачи. В ней дан механизм, состоящий из колес, рейки и груза, соединенных нитями и зубчатой передачей. Требуется найти скорости и ускорения точек, принадлежащих звеньям этого механизма. Кинематический анализ плоского механизма – пример решения задачи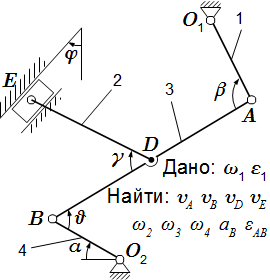 Рассмотрены методы определения скоростей и ускорений звеньев плоского многозвенного механизма. При этом используется понятие мгновенного центра скоростей, теоремы о проекциях скоростей, о скоростях точек и об ускорениях точек плоской фигуры. Подробно разобран пример решения задачи на тему 'кинематический анализ многозвенного механизма'. Сложное движение точки. Теорема Кориолиса
Рассмотрены методы определения скоростей и ускорений звеньев плоского многозвенного механизма. При этом используется понятие мгновенного центра скоростей, теоремы о проекциях скоростей, о скоростях точек и об ускорениях точек плоской фигуры. Подробно разобран пример решения задачи на тему 'кинематический анализ многозвенного механизма'. Сложное движение точки. Теорема Кориолиса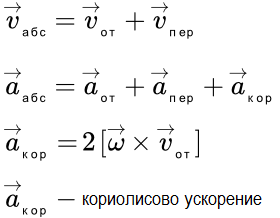 Определение сложного (составного) движения точки. Определение абсолютного, относительного и переносного движения, скорости и ускорения. Доказательство теоремы о сложении скоростей и теоремы Кориолиса о сложении ускорений. Кориолисово (поворотное) ускорение. Сложное движение точки. Пример решения задачи
Определение сложного (составного) движения точки. Определение абсолютного, относительного и переносного движения, скорости и ускорения. Доказательство теоремы о сложении скоростей и теоремы Кориолиса о сложении ускорений. Кориолисово (поворотное) ускорение. Сложное движение точки. Пример решения задачи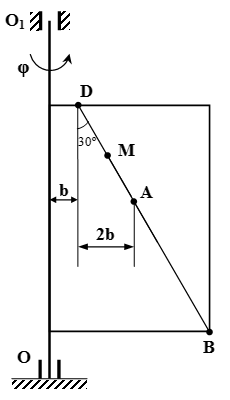 Рассмотрен пример решения задачи со сложным движением точки. Точка движется по прямой вдоль пластины. Пластина вращается вокруг неподвижной оси. Определяется абсолютная скорость и абсолютное ускорение точки.
Рассмотрен пример решения задачи со сложным движением точки. Точка движется по прямой вдоль пластины. Пластина вращается вокруг неподвижной оси. Определяется абсолютная скорость и абсолютное ускорение точки.
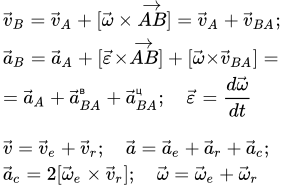 Все определения, понятия, законы и теоремы кинематики в одной странице. Материал делится на четыре основных раздела: кинематика точки, кинематика твердого тела, кинематика сложного движения точки и кинематика сложного движения твердого тела. Все картинки раздела «Кинематика»
Все определения, понятия, законы и теоремы кинематики в одной странице. Материал делится на четыре основных раздела: кинематика точки, кинематика твердого тела, кинематика сложного движения точки и кинематика сложного движения твердого тела. Все картинки раздела «Кинематика» Здесь собраны все изображения раздела «Кинематика» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Что такое радиус-вектор, и чем он отличается от других векторов
Здесь собраны все изображения раздела «Кинематика» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Что такое радиус-вектор, и чем он отличается от других векторов Понятие радиус-вектора и его свойства. На примерах разобрано его отличие от других векторов. Кинематика материальной точки
Понятие радиус-вектора и его свойства. На примерах разобрано его отличие от других векторов. Кинематика материальной точки Даны основные формулы кинематики материальной точки, их вывод и изложение теории. Координатный способ задания движения точки
Даны основные формулы кинематики материальной точки, их вывод и изложение теории. Координатный способ задания движения точки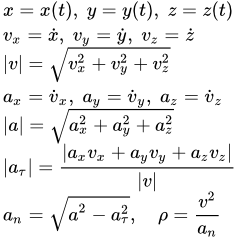 Формулы для вычисления скорости точки, ускорения, радиуса кривизны траектории, касательной, нормали и бинормали по заданным зависимостям координат от времени. Пример решения задачи, в которой по заданным уравнениям движения нужно определить скорость и ускорение точки. Также определяется радиус кривизны траектории, касательная, нормаль и бинормаль. Векторный способ задания движения точки
Формулы для вычисления скорости точки, ускорения, радиуса кривизны траектории, касательной, нормали и бинормали по заданным зависимостям координат от времени. Пример решения задачи, в которой по заданным уравнениям движения нужно определить скорость и ускорение точки. Также определяется радиус кривизны траектории, касательная, нормаль и бинормаль. Векторный способ задания движения точки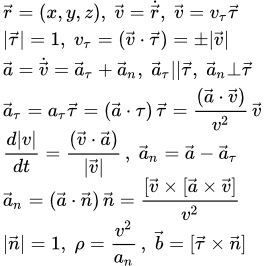 Связь векторного способа задания движения точки с координатным. Формулы для вычисления скорости точки, ускорения, радиуса кривизны траектории, касательной, нормали и бинормали при векторном способе задания движения точки. Оси естественного трехгранника Френе
Связь векторного способа задания движения точки с координатным. Формулы для вычисления скорости точки, ускорения, радиуса кривизны траектории, касательной, нормали и бинормали при векторном способе задания движения точки. Оси естественного трехгранника Френе Определение естественного трехгранника Френе. Проекции скорости и ускорения точки на его оси. Пример определения ортов естественного трехгранника. Естественный способ задания движения точки
Определение естественного трехгранника Френе. Проекции скорости и ускорения точки на его оси. Пример определения ортов естественного трехгранника. Естественный способ задания движения точки Естественный способ задания движения точки – определение и основные формулы. Пример решения задачи. Теорема о проекциях скоростей двух точек твердого тела на прямую
Естественный способ задания движения точки – определение и основные формулы. Пример решения задачи. Теорема о проекциях скоростей двух точек твердого тела на прямую Теорема о проекциях скоростей двух точек твердого тела на прямую. Доказательство теоремы. Пример решения задачи. Скорость и ускорение точек твердого тела, совершающего поступательное и вращательное движения
Теорема о проекциях скоростей двух точек твердого тела на прямую. Доказательство теоремы. Пример решения задачи. Скорость и ускорение точек твердого тела, совершающего поступательное и вращательное движения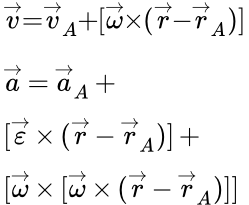 Формулы скорости (ускорения) точек твердого тела, выраженные через скорость (ускорение) полюса и угловую скорость (ускорение). Вывод этих формул из принципа, что расстояния между любыми точками тела, при его движении, остаются постоянными. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи
Формулы скорости (ускорения) точек твердого тела, выраженные через скорость (ускорение) полюса и угловую скорость (ускорение). Вывод этих формул из принципа, что расстояния между любыми точками тела, при его движении, остаются постоянными. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи Приводятся основные законы и формулы, применяемые при решении задач на определение скоростей и ускорений точек твердого тела при вращательном движении вокруг неподвижной оси. Рассмотрен пример подробного решения задачи. В ней дан механизм, состоящий из колес, рейки и груза, соединенных нитями и зубчатой передачей. Требуется найти скорости и ускорения точек, принадлежащих звеньям этого механизма. Кинематический анализ плоского механизма – пример решения задачи
Приводятся основные законы и формулы, применяемые при решении задач на определение скоростей и ускорений точек твердого тела при вращательном движении вокруг неподвижной оси. Рассмотрен пример подробного решения задачи. В ней дан механизм, состоящий из колес, рейки и груза, соединенных нитями и зубчатой передачей. Требуется найти скорости и ускорения точек, принадлежащих звеньям этого механизма. Кинематический анализ плоского механизма – пример решения задачи Рассмотрены методы определения скоростей и ускорений звеньев плоского многозвенного механизма. При этом используется понятие мгновенного центра скоростей, теоремы о проекциях скоростей, о скоростях точек и об ускорениях точек плоской фигуры. Подробно разобран пример решения задачи на тему 'кинематический анализ многозвенного механизма'. Сложное движение точки. Теорема Кориолиса
Рассмотрены методы определения скоростей и ускорений звеньев плоского многозвенного механизма. При этом используется понятие мгновенного центра скоростей, теоремы о проекциях скоростей, о скоростях точек и об ускорениях точек плоской фигуры. Подробно разобран пример решения задачи на тему 'кинематический анализ многозвенного механизма'. Сложное движение точки. Теорема Кориолиса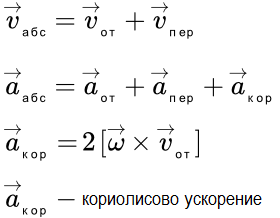 Определение сложного (составного) движения точки. Определение абсолютного, относительного и переносного движения, скорости и ускорения. Доказательство теоремы о сложении скоростей и теоремы Кориолиса о сложении ускорений. Кориолисово (поворотное) ускорение. Сложное движение точки. Пример решения задачи
Определение сложного (составного) движения точки. Определение абсолютного, относительного и переносного движения, скорости и ускорения. Доказательство теоремы о сложении скоростей и теоремы Кориолиса о сложении ускорений. Кориолисово (поворотное) ускорение. Сложное движение точки. Пример решения задачи Рассмотрен пример решения задачи со сложным движением точки. Точка движется по прямой вдоль пластины. Пластина вращается вокруг неподвижной оси. Определяется абсолютная скорость и абсолютное ускорение точки.
Рассмотрен пример решения задачи со сложным движением точки. Точка движется по прямой вдоль пластины. Пластина вращается вокруг неподвижной оси. Определяется абсолютная скорость и абсолютное ускорение точки. Динамика
Динамика материальной точки. Все законы и теоремы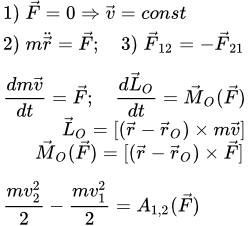 Все понятия, определения, законы и теоремы динамики материальной точки в одной странице. Материал делится на следующие разделы: основные законы динамики точки (законы Ньютона), виды сил, дифференциальные уравнения движения, колебания, общие теоремы динамики точки, силовые поля и потенциальная энергия. Все картинки раздела «Динамика материальной точки»
Все понятия, определения, законы и теоремы динамики материальной точки в одной странице. Материал делится на следующие разделы: основные законы динамики точки (законы Ньютона), виды сил, дифференциальные уравнения движения, колебания, общие теоремы динамики точки, силовые поля и потенциальная энергия. Все картинки раздела «Динамика материальной точки»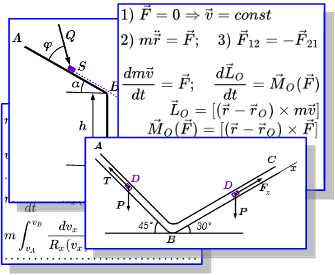 Здесь собраны все изображения раздела «Динамика материальной точки» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Определение понятия материальной точки
Здесь собраны все изображения раздела «Динамика материальной точки» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Определение понятия материальной точки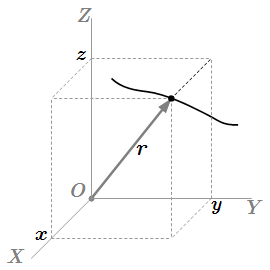 Понятие и определение материальной точки как самого простого тела в механике. Применимость этого понятия к телам с конечными размерами в различных задачах. Примеры. Интегрирование дифференциальных уравнений прямолинейного движения материальной точки
Понятие и определение материальной точки как самого простого тела в механике. Применимость этого понятия к телам с конечными размерами в различных задачах. Примеры. Интегрирование дифференциальных уравнений прямолинейного движения материальной точки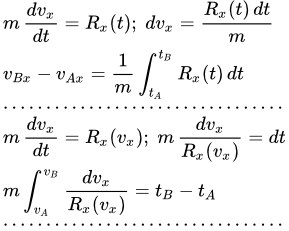 Даны методы интегрирования дифференциальных уравнений прямолинейного движения материальной точки. Рассмотрены случаи, когда равнодействующая сила зависит от времени, скорости и перемещения. При зависимости силы от скорости, даны два способа решения. В случае зависимости силы от перемещения, интегрирование приводит к закону сохранения механической энергии. Рассмотрено приложение этих методов к движению в пространстве. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил
Даны методы интегрирования дифференциальных уравнений прямолинейного движения материальной точки. Рассмотрены случаи, когда равнодействующая сила зависит от времени, скорости и перемещения. При зависимости силы от скорости, даны два способа решения. В случае зависимости силы от перемещения, интегрирование приводит к закону сохранения механической энергии. Рассмотрено приложение этих методов к движению в пространстве. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил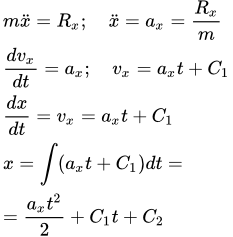 Рассмотрен метод интегрирования дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил. Приводится пример решения задачи на движение материальной точки, на которую действуют только постоянные силы. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил
Рассмотрен метод интегрирования дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил. Приводится пример решения задачи на движение материальной точки, на которую действуют только постоянные силы. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил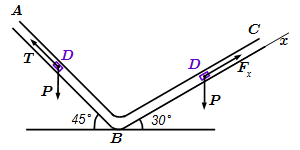 Рассмотрено решение задачи, в которой материальная точка движется по изогнутой трубе с двумя прямолинейными участками. При этом, кроме силы тяжести и реакций стенок трубы, на первом участке, на точку действует постоянная сила, и сила сопротивления среды, зависящая от скорости; на втором участке – внешняя сила, изменяющаяся со временем. Динамика твердого тела и системы. Все определения, законы и теоремы
Рассмотрено решение задачи, в которой материальная точка движется по изогнутой трубе с двумя прямолинейными участками. При этом, кроме силы тяжести и реакций стенок трубы, на первом участке, на точку действует постоянная сила, и сила сопротивления среды, зависящая от скорости; на втором участке – внешняя сила, изменяющаяся со временем. Динамика твердого тела и системы. Все определения, законы и теоремы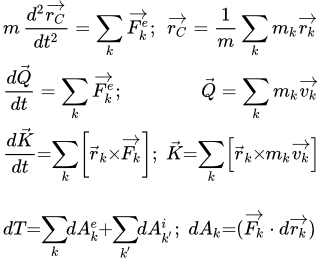 Все понятия, определения, законы, теоремы и свойства динамики твердого тела и системы. Общие теоремы динамики системы. Теоремы о движении центра масс, об изменении количества движения, об изменении главного момента количества движения, об изменении кинетической энергии. Принципы Даламбера, и возможных перемещений. Общее уравнение динамики. Уравнения Лагранжа. Все картинки раздела «Динамика твердого тела и системы»
Все понятия, определения, законы, теоремы и свойства динамики твердого тела и системы. Общие теоремы динамики системы. Теоремы о движении центра масс, об изменении количества движения, об изменении главного момента количества движения, об изменении кинетической энергии. Принципы Даламбера, и возможных перемещений. Общее уравнение динамики. Уравнения Лагранжа. Все картинки раздела «Динамика твердого тела и системы»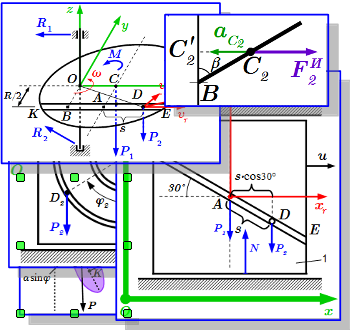 Здесь собраны все изображения раздела «Динамика твердого тела и системы» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Понятие механических связей и их классификация
Здесь собраны все изображения раздела «Динамика твердого тела и системы» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Понятие механических связей и их классификация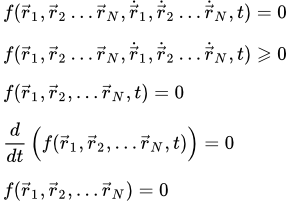 Дается определение понятия механических связей, и излагаются физические принципы их возникновения. Даны определения основных видов связей, применяемых в теоретической механике, и приводится их классификация. Рассмотрены примеры связей различных типов. Теорема о движении центра масс системы. Решение задач
Дается определение понятия механических связей, и излагаются физические принципы их возникновения. Даны определения основных видов связей, применяемых в теоретической механике, и приводится их классификация. Рассмотрены примеры связей различных типов. Теорема о движении центра масс системы. Решение задач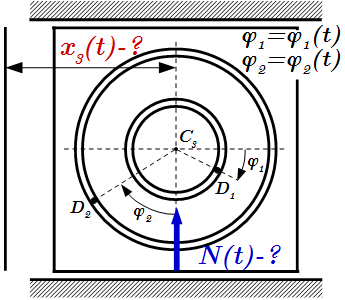 Приводятся формулы и законы, применяемые при решении задач с помощью теоремы о движении центра масс системы. Рассмотрены примеры решения задач. В одной задаче требуется найти смещение плиты с движущимися по ней грузами и реакцию направляющих. В другой задаче нужно найти вертикальную составляющую реакции в точке крепления кривошипно-шатунного механизма с ползуном. Решение задач на применение теоремы об изменении количества движения системы
Приводятся формулы и законы, применяемые при решении задач с помощью теоремы о движении центра масс системы. Рассмотрены примеры решения задач. В одной задаче требуется найти смещение плиты с движущимися по ней грузами и реакцию направляющих. В другой задаче нужно найти вертикальную составляющую реакции в точке крепления кривошипно-шатунного механизма с ползуном. Решение задач на применение теоремы об изменении количества движения системы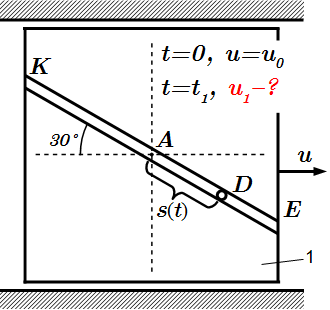 Приводится инструкция, как решать задачи на применение теоремы об изменении количества движения системы. Рассмотрен пример решения задачи. Решение задач на применение теоремы об изменении кинетического момента системы
Приводится инструкция, как решать задачи на применение теоремы об изменении количества движения системы. Рассмотрен пример решения задачи. Решение задач на применение теоремы об изменении кинетического момента системы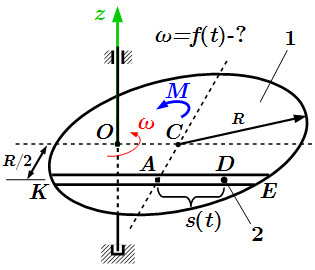 Инструкция о порядке решения задач на применение теоремы об изменении кинетического момента системы. Рассмотрены примеры решения задач с краткими и подробными решениями. Теорема об изменении кинетической энергии. Пример решения задачи.
Инструкция о порядке решения задач на применение теоремы об изменении кинетического момента системы. Рассмотрены примеры решения задач с краткими и подробными решениями. Теорема об изменении кинетической энергии. Пример решения задачи.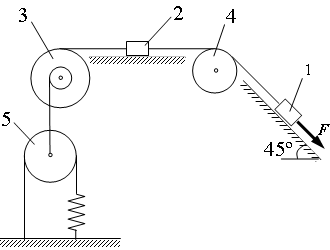 Пример решения задачи с применением теоремы об изменении кинетической энергии системы с твердыми телами, блоками, шкивами и пружиной. Общее уравнение динамики. Пример решения задачи
Пример решения задачи с применением теоремы об изменении кинетической энергии системы с твердыми телами, блоками, шкивами и пружиной. Общее уравнение динамики. Пример решения задачи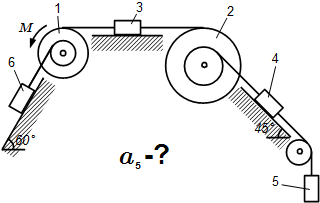 Пример решения задачи с применением общего уравнения динамики (принцип Даламбера – Лагранжа) для системы с твердыми телами, грузами, шкивами и блоком, соединенных нитями. Принцип Даламбера (кинетостатика). Решение задачи
Пример решения задачи с применением общего уравнения динамики (принцип Даламбера – Лагранжа) для системы с твердыми телами, грузами, шкивами и блоком, соединенных нитями. Принцип Даламбера (кинетостатика). Решение задачи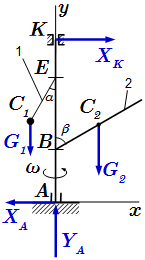 Рассмотрены законы, применяемые при решении задач методом кинетостатики. Приводится пример решения задачи, используя принцип Даламбера на определение реакций опор вращающегося вала. Приводится решение задачи двумя способами – применяя принцип Даламбера к стержню как к системе материальных точек, и как к твердому телу.
Рассмотрены законы, применяемые при решении задач методом кинетостатики. Приводится пример решения задачи, используя принцип Даламбера на определение реакций опор вращающегося вала. Приводится решение задачи двумя способами – применяя принцип Даламбера к стержню как к системе материальных точек, и как к твердому телу.
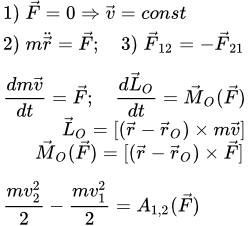 Все понятия, определения, законы и теоремы динамики материальной точки в одной странице. Материал делится на следующие разделы: основные законы динамики точки (законы Ньютона), виды сил, дифференциальные уравнения движения, колебания, общие теоремы динамики точки, силовые поля и потенциальная энергия. Все картинки раздела «Динамика материальной точки»
Все понятия, определения, законы и теоремы динамики материальной точки в одной странице. Материал делится на следующие разделы: основные законы динамики точки (законы Ньютона), виды сил, дифференциальные уравнения движения, колебания, общие теоремы динамики точки, силовые поля и потенциальная энергия. Все картинки раздела «Динамика материальной точки» Здесь собраны все изображения раздела «Динамика материальной точки» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Определение понятия материальной точки
Здесь собраны все изображения раздела «Динамика материальной точки» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Определение понятия материальной точки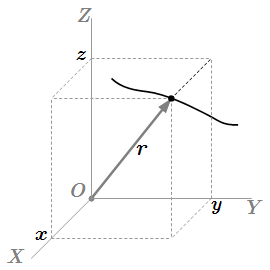 Понятие и определение материальной точки как самого простого тела в механике. Применимость этого понятия к телам с конечными размерами в различных задачах. Примеры. Интегрирование дифференциальных уравнений прямолинейного движения материальной точки
Понятие и определение материальной точки как самого простого тела в механике. Применимость этого понятия к телам с конечными размерами в различных задачах. Примеры. Интегрирование дифференциальных уравнений прямолинейного движения материальной точки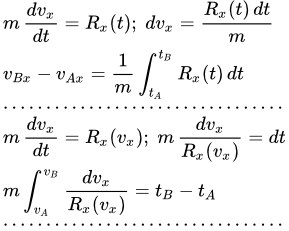 Даны методы интегрирования дифференциальных уравнений прямолинейного движения материальной точки. Рассмотрены случаи, когда равнодействующая сила зависит от времени, скорости и перемещения. При зависимости силы от скорости, даны два способа решения. В случае зависимости силы от перемещения, интегрирование приводит к закону сохранения механической энергии. Рассмотрено приложение этих методов к движению в пространстве. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил
Даны методы интегрирования дифференциальных уравнений прямолинейного движения материальной точки. Рассмотрены случаи, когда равнодействующая сила зависит от времени, скорости и перемещения. При зависимости силы от скорости, даны два способа решения. В случае зависимости силы от перемещения, интегрирование приводит к закону сохранения механической энергии. Рассмотрено приложение этих методов к движению в пространстве. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил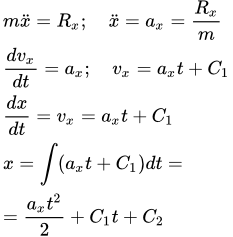 Рассмотрен метод интегрирования дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил. Приводится пример решения задачи на движение материальной точки, на которую действуют только постоянные силы. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил
Рассмотрен метод интегрирования дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил. Приводится пример решения задачи на движение материальной точки, на которую действуют только постоянные силы. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил Рассмотрено решение задачи, в которой материальная точка движется по изогнутой трубе с двумя прямолинейными участками. При этом, кроме силы тяжести и реакций стенок трубы, на первом участке, на точку действует постоянная сила, и сила сопротивления среды, зависящая от скорости; на втором участке – внешняя сила, изменяющаяся со временем. Динамика твердого тела и системы. Все определения, законы и теоремы
Рассмотрено решение задачи, в которой материальная точка движется по изогнутой трубе с двумя прямолинейными участками. При этом, кроме силы тяжести и реакций стенок трубы, на первом участке, на точку действует постоянная сила, и сила сопротивления среды, зависящая от скорости; на втором участке – внешняя сила, изменяющаяся со временем. Динамика твердого тела и системы. Все определения, законы и теоремы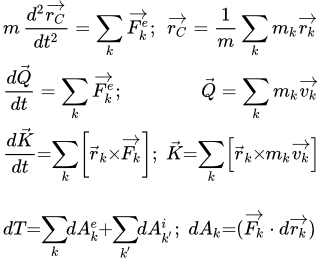 Все понятия, определения, законы, теоремы и свойства динамики твердого тела и системы. Общие теоремы динамики системы. Теоремы о движении центра масс, об изменении количества движения, об изменении главного момента количества движения, об изменении кинетической энергии. Принципы Даламбера, и возможных перемещений. Общее уравнение динамики. Уравнения Лагранжа. Все картинки раздела «Динамика твердого тела и системы»
Все понятия, определения, законы, теоремы и свойства динамики твердого тела и системы. Общие теоремы динамики системы. Теоремы о движении центра масс, об изменении количества движения, об изменении главного момента количества движения, об изменении кинетической энергии. Принципы Даламбера, и возможных перемещений. Общее уравнение динамики. Уравнения Лагранжа. Все картинки раздела «Динамика твердого тела и системы» Здесь собраны все изображения раздела «Динамика твердого тела и системы» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Понятие механических связей и их классификация
Здесь собраны все изображения раздела «Динамика твердого тела и системы» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Понятие механических связей и их классификация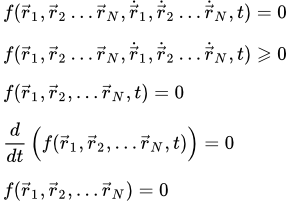 Дается определение понятия механических связей, и излагаются физические принципы их возникновения. Даны определения основных видов связей, применяемых в теоретической механике, и приводится их классификация. Рассмотрены примеры связей различных типов. Теорема о движении центра масс системы. Решение задач
Дается определение понятия механических связей, и излагаются физические принципы их возникновения. Даны определения основных видов связей, применяемых в теоретической механике, и приводится их классификация. Рассмотрены примеры связей различных типов. Теорема о движении центра масс системы. Решение задач Приводятся формулы и законы, применяемые при решении задач с помощью теоремы о движении центра масс системы. Рассмотрены примеры решения задач. В одной задаче требуется найти смещение плиты с движущимися по ней грузами и реакцию направляющих. В другой задаче нужно найти вертикальную составляющую реакции в точке крепления кривошипно-шатунного механизма с ползуном. Решение задач на применение теоремы об изменении количества движения системы
Приводятся формулы и законы, применяемые при решении задач с помощью теоремы о движении центра масс системы. Рассмотрены примеры решения задач. В одной задаче требуется найти смещение плиты с движущимися по ней грузами и реакцию направляющих. В другой задаче нужно найти вертикальную составляющую реакции в точке крепления кривошипно-шатунного механизма с ползуном. Решение задач на применение теоремы об изменении количества движения системы Приводится инструкция, как решать задачи на применение теоремы об изменении количества движения системы. Рассмотрен пример решения задачи. Решение задач на применение теоремы об изменении кинетического момента системы
Приводится инструкция, как решать задачи на применение теоремы об изменении количества движения системы. Рассмотрен пример решения задачи. Решение задач на применение теоремы об изменении кинетического момента системы Инструкция о порядке решения задач на применение теоремы об изменении кинетического момента системы. Рассмотрены примеры решения задач с краткими и подробными решениями. Теорема об изменении кинетической энергии. Пример решения задачи.
Инструкция о порядке решения задач на применение теоремы об изменении кинетического момента системы. Рассмотрены примеры решения задач с краткими и подробными решениями. Теорема об изменении кинетической энергии. Пример решения задачи. Пример решения задачи с применением теоремы об изменении кинетической энергии системы с твердыми телами, блоками, шкивами и пружиной. Общее уравнение динамики. Пример решения задачи
Пример решения задачи с применением теоремы об изменении кинетической энергии системы с твердыми телами, блоками, шкивами и пружиной. Общее уравнение динамики. Пример решения задачи Пример решения задачи с применением общего уравнения динамики (принцип Даламбера – Лагранжа) для системы с твердыми телами, грузами, шкивами и блоком, соединенных нитями. Принцип Даламбера (кинетостатика). Решение задачи
Пример решения задачи с применением общего уравнения динамики (принцип Даламбера – Лагранжа) для системы с твердыми телами, грузами, шкивами и блоком, соединенных нитями. Принцип Даламбера (кинетостатика). Решение задачи Рассмотрены законы, применяемые при решении задач методом кинетостатики. Приводится пример решения задачи, используя принцип Даламбера на определение реакций опор вращающегося вала. Приводится решение задачи двумя способами – применяя принцип Даламбера к стержню как к системе материальных точек, и как к твердому телу.
Рассмотрены законы, применяемые при решении задач методом кинетостатики. Приводится пример решения задачи, используя принцип Даламбера на определение реакций опор вращающегося вала. Приводится решение задачи двумя способами – применяя принцип Даламбера к стержню как к системе материальных точек, и как к твердому телу. Статика
Статика – все понятия, определения, законы и теоремы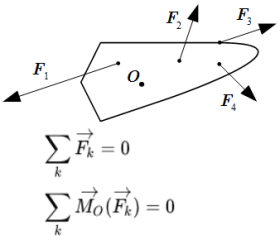 Все понятия и законы статики на одной странице, включая определения, аксиомы, теоремы и свойства. Все картинки раздела «Статика»
Все понятия и законы статики на одной странице, включая определения, аксиомы, теоремы и свойства. Все картинки раздела «Статика»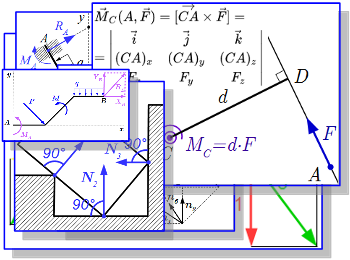 Здесь собраны все изображения раздела «Статика» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Основные понятия и определения статики
Здесь собраны все изображения раздела «Статика» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Основные понятия и определения статики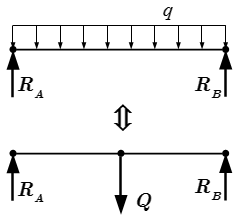 Изложены основные понятия и определения статики – раздела теоретической механики. Рассмотрена основная задача статики и область ее применения. Даны определения, связанные с системами тел, кинематическим состоянием тела и действующими силами. Силы в теоретической механике
Изложены основные понятия и определения статики – раздела теоретической механики. Рассмотрена основная задача статики и область ее применения. Даны определения, связанные с системами тел, кинематическим состоянием тела и действующими силами. Силы в теоретической механике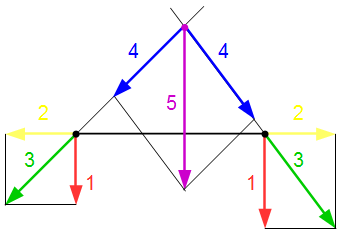 Дано определение силы, действующей на материальную точку. Показано, что в теоретической механике, в задачах на определение движения твердых тел, силы являются скользящими векторами. Поэтому системы сил можно преобразовывать в более простые эквивалентные системы. Показано, что получить эквивалентную систему, можно решая задачу статики, в которой к старой системе добавляется новая система сил. Аксиомы статики
Дано определение силы, действующей на материальную точку. Показано, что в теоретической механике, в задачах на определение движения твердых тел, силы являются скользящими векторами. Поэтому системы сил можно преобразовывать в более простые эквивалентные системы. Показано, что получить эквивалентную систему, можно решая задачу статики, в которой к старой системе добавляется новая система сил. Аксиомы статики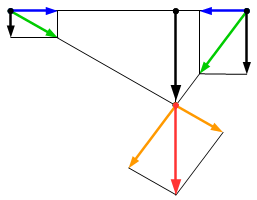 Изложены аксиомы статики. Пояснена их роль в теоретической механике. Приводится пример графического решения задачи, применяя только аксиомы статики. Определение и свойства момента силы
Изложены аксиомы статики. Пояснена их роль в теоретической механике. Приводится пример графического решения задачи, применяя только аксиомы статики. Определение и свойства момента силы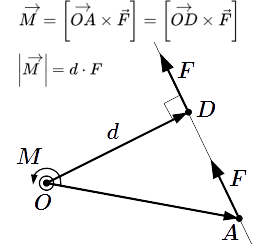 Определения и свойства момента силы относительно точки и оси. Определение плеча силы. Выражение абсолютного значения момента в виде произведения плеча на модуль силы. Способы расчета момента силы относительно точки и оси
Определения и свойства момента силы относительно точки и оси. Определение плеча силы. Выражение абсолютного значения момента в виде произведения плеча на модуль силы. Способы расчета момента силы относительно точки и оси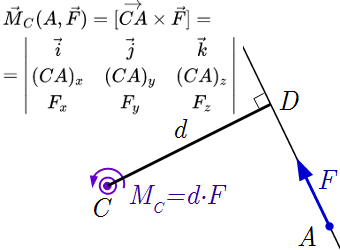 Рассмотрены способы определения момента силы относительно точки и оси. Приедены примеры расчетов. Условия равновесия твердого тела и системы сил
Рассмотрены способы определения момента силы относительно точки и оси. Приедены примеры расчетов. Условия равновесия твердого тела и системы сил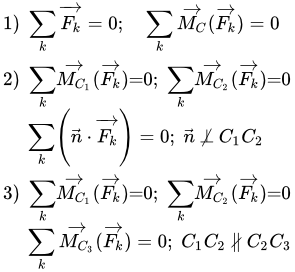 Обсуждается связь между понятиями "равновесие твердого тела" и "равновесие системы сил". Приводятся три формы условий равновесия твердого тела, как для пространственной системы сил, так и для плоской. Дано доказательство всех форм условий равновесия. Равнодействующая системы двух параллельных сил
Обсуждается связь между понятиями "равновесие твердого тела" и "равновесие системы сил". Приводятся три формы условий равновесия твердого тела, как для пространственной системы сил, так и для плоской. Дано доказательство всех форм условий равновесия. Равнодействующая системы двух параллельных сил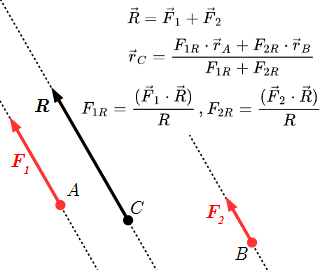 Расчет равнодействующей системы двух параллельных сил тремя способами, используя аксиомы статики и уравнения равновесия. Центр системы параллельных сил
Расчет равнодействующей системы двух параллельных сил тремя способами, используя аксиомы статики и уравнения равновесия. Центр системы параллельных сил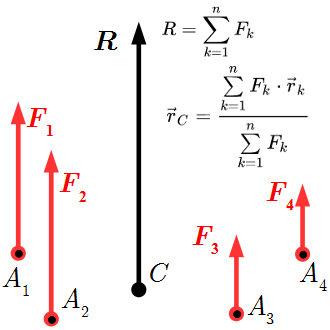 Определение центра параллельных сил. Доказано двумя способами, что система сил, параллельных некоторой оси, векторная сумма которых не равна нулю, имеет равнодействующую, проходящую через центр параллельных сил. Аксиома связей (принцип освобождаемости от связей)
Определение центра параллельных сил. Доказано двумя способами, что система сил, параллельных некоторой оси, векторная сумма которых не равна нулю, имеет равнодействующую, проходящую через центр параллельных сил. Аксиома связей (принцип освобождаемости от связей)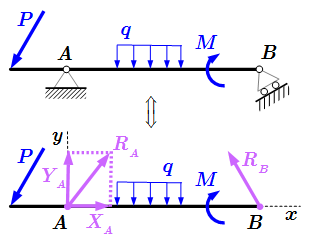 Формулировка принципа освобождаемости от связей, который часто называется аксиомой связей. Показано, что аксиома связей является следствием основных законов механики. Даны определения активных и пассивных сил. Рассмотрено применение принципа освобождаемости от связей для решения механических задач, в которых тела соединены друг с другом и с неподвижным основанием. Примеры приведения таких задач к задаче со свободными телами. Основные типы связей и их реакции, применяемые в технической механике
Формулировка принципа освобождаемости от связей, который часто называется аксиомой связей. Показано, что аксиома связей является следствием основных законов механики. Даны определения активных и пассивных сил. Рассмотрено применение принципа освобождаемости от связей для решения механических задач, в которых тела соединены друг с другом и с неподвижным основанием. Примеры приведения таких задач к задаче со свободными телами. Основные типы связей и их реакции, применяемые в технической механике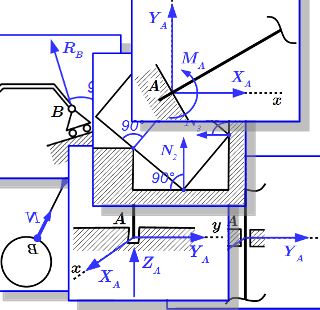 Приводятся основные виды связей и их реакции, применяемые в технической механике при проектировании машин и механизмов. Даны их условные обозначения и направления сил реакций. Методы определения реакций опор твердого тела
Приводятся основные виды связей и их реакции, применяемые в технической механике при проектировании машин и механизмов. Даны их условные обозначения и направления сил реакций. Методы определения реакций опор твердого тела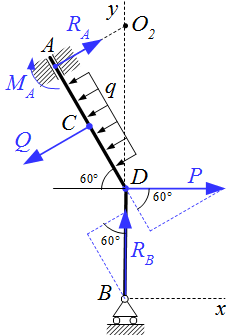 Рассмотрены методы определения реакций опор твердого тела для статически определимых схем закреплений тел в опорах. Определение реакций опор твердого тела – решение задачи
Рассмотрены методы определения реакций опор твердого тела для статически определимых схем закреплений тел в опорах. Определение реакций опор твердого тела – решение задачи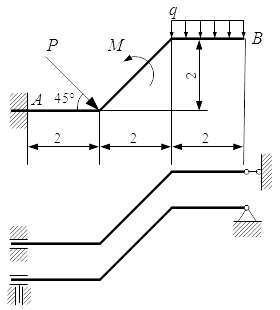 Приводится решение задачи, в которой требуемая реакция опоры твердого тела определяется из одного уравнения, без определения остальных сил реакций. Для трех вариантов закрепления тела выбирается тот, при котором требуемая реакция имеет наименьшее значение. Для этого варианта определяются реакции остальных опор. Определение реакций опор балки – решение задачи
Приводится решение задачи, в которой требуемая реакция опоры твердого тела определяется из одного уравнения, без определения остальных сил реакций. Для трех вариантов закрепления тела выбирается тот, при котором требуемая реакция имеет наименьшее значение. Для этого варианта определяются реакции остальных опор. Определение реакций опор балки – решение задачи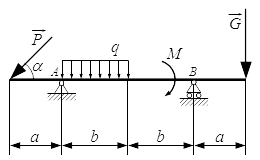 Рассмотрен порядок решения задач на определение реакций опор балок. Приводится пример решения задачи двумя способами и проверка правильности определения реакций. Определение реакций опор составной конструкции – решение задачи
Рассмотрен порядок решения задач на определение реакций опор балок. Приводится пример решения задачи двумя способами и проверка правильности определения реакций. Определение реакций опор составной конструкции – решение задачи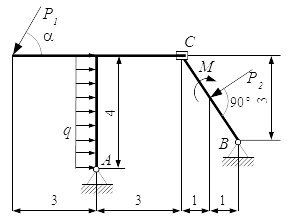 Рассмотрен метод решения задач на определение реакций опор составных конструкций для статически определимых систем. Приводится пример решения задачи, в которой требуется определить реакции в опорах и в точке соединения частей составной конструкции. Определение реакций стержней, поддерживающих прямоугольную плиту – решение задачи
Рассмотрен метод решения задач на определение реакций опор составных конструкций для статически определимых систем. Приводится пример решения задачи, в которой требуется определить реакции в опорах и в точке соединения частей составной конструкции. Определение реакций стержней, поддерживающих прямоугольную плиту – решение задачи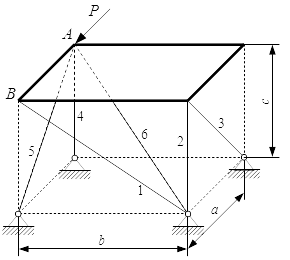 Рассмотрены методы решения задач на равновесие с произвольной пространственной системой сил. Приводится пример решения задачи на равновесие плиты, поддерживаемой стержнями в трехмерном пространстве. Показано, как за счет выбора осей при составлении уравнений равновесия, можно упростить решение задачи.
Рассмотрены методы решения задач на равновесие с произвольной пространственной системой сил. Приводится пример решения задачи на равновесие плиты, поддерживаемой стержнями в трехмерном пространстве. Показано, как за счет выбора осей при составлении уравнений равновесия, можно упростить решение задачи.
 Все понятия и законы статики на одной странице, включая определения, аксиомы, теоремы и свойства. Все картинки раздела «Статика»
Все понятия и законы статики на одной странице, включая определения, аксиомы, теоремы и свойства. Все картинки раздела «Статика» Здесь собраны все изображения раздела «Статика» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Основные понятия и определения статики
Здесь собраны все изображения раздела «Статика» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением. Основные понятия и определения статики Изложены основные понятия и определения статики – раздела теоретической механики. Рассмотрена основная задача статики и область ее применения. Даны определения, связанные с системами тел, кинематическим состоянием тела и действующими силами. Силы в теоретической механике
Изложены основные понятия и определения статики – раздела теоретической механики. Рассмотрена основная задача статики и область ее применения. Даны определения, связанные с системами тел, кинематическим состоянием тела и действующими силами. Силы в теоретической механике Дано определение силы, действующей на материальную точку. Показано, что в теоретической механике, в задачах на определение движения твердых тел, силы являются скользящими векторами. Поэтому системы сил можно преобразовывать в более простые эквивалентные системы. Показано, что получить эквивалентную систему, можно решая задачу статики, в которой к старой системе добавляется новая система сил. Аксиомы статики
Дано определение силы, действующей на материальную точку. Показано, что в теоретической механике, в задачах на определение движения твердых тел, силы являются скользящими векторами. Поэтому системы сил можно преобразовывать в более простые эквивалентные системы. Показано, что получить эквивалентную систему, можно решая задачу статики, в которой к старой системе добавляется новая система сил. Аксиомы статики Изложены аксиомы статики. Пояснена их роль в теоретической механике. Приводится пример графического решения задачи, применяя только аксиомы статики. Определение и свойства момента силы
Изложены аксиомы статики. Пояснена их роль в теоретической механике. Приводится пример графического решения задачи, применяя только аксиомы статики. Определение и свойства момента силы Определения и свойства момента силы относительно точки и оси. Определение плеча силы. Выражение абсолютного значения момента в виде произведения плеча на модуль силы. Способы расчета момента силы относительно точки и оси
Определения и свойства момента силы относительно точки и оси. Определение плеча силы. Выражение абсолютного значения момента в виде произведения плеча на модуль силы. Способы расчета момента силы относительно точки и оси Рассмотрены способы определения момента силы относительно точки и оси. Приедены примеры расчетов. Условия равновесия твердого тела и системы сил
Рассмотрены способы определения момента силы относительно точки и оси. Приедены примеры расчетов. Условия равновесия твердого тела и системы сил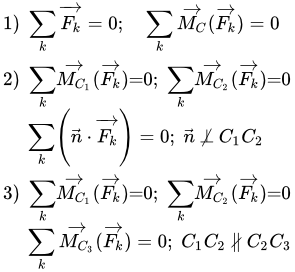 Обсуждается связь между понятиями "равновесие твердого тела" и "равновесие системы сил". Приводятся три формы условий равновесия твердого тела, как для пространственной системы сил, так и для плоской. Дано доказательство всех форм условий равновесия. Равнодействующая системы двух параллельных сил
Обсуждается связь между понятиями "равновесие твердого тела" и "равновесие системы сил". Приводятся три формы условий равновесия твердого тела, как для пространственной системы сил, так и для плоской. Дано доказательство всех форм условий равновесия. Равнодействующая системы двух параллельных сил Расчет равнодействующей системы двух параллельных сил тремя способами, используя аксиомы статики и уравнения равновесия. Центр системы параллельных сил
Расчет равнодействующей системы двух параллельных сил тремя способами, используя аксиомы статики и уравнения равновесия. Центр системы параллельных сил Определение центра параллельных сил. Доказано двумя способами, что система сил, параллельных некоторой оси, векторная сумма которых не равна нулю, имеет равнодействующую, проходящую через центр параллельных сил. Аксиома связей (принцип освобождаемости от связей)
Определение центра параллельных сил. Доказано двумя способами, что система сил, параллельных некоторой оси, векторная сумма которых не равна нулю, имеет равнодействующую, проходящую через центр параллельных сил. Аксиома связей (принцип освобождаемости от связей) Формулировка принципа освобождаемости от связей, который часто называется аксиомой связей. Показано, что аксиома связей является следствием основных законов механики. Даны определения активных и пассивных сил. Рассмотрено применение принципа освобождаемости от связей для решения механических задач, в которых тела соединены друг с другом и с неподвижным основанием. Примеры приведения таких задач к задаче со свободными телами. Основные типы связей и их реакции, применяемые в технической механике
Формулировка принципа освобождаемости от связей, который часто называется аксиомой связей. Показано, что аксиома связей является следствием основных законов механики. Даны определения активных и пассивных сил. Рассмотрено применение принципа освобождаемости от связей для решения механических задач, в которых тела соединены друг с другом и с неподвижным основанием. Примеры приведения таких задач к задаче со свободными телами. Основные типы связей и их реакции, применяемые в технической механике Приводятся основные виды связей и их реакции, применяемые в технической механике при проектировании машин и механизмов. Даны их условные обозначения и направления сил реакций. Методы определения реакций опор твердого тела
Приводятся основные виды связей и их реакции, применяемые в технической механике при проектировании машин и механизмов. Даны их условные обозначения и направления сил реакций. Методы определения реакций опор твердого тела Рассмотрены методы определения реакций опор твердого тела для статически определимых схем закреплений тел в опорах. Определение реакций опор твердого тела – решение задачи
Рассмотрены методы определения реакций опор твердого тела для статически определимых схем закреплений тел в опорах. Определение реакций опор твердого тела – решение задачи Приводится решение задачи, в которой требуемая реакция опоры твердого тела определяется из одного уравнения, без определения остальных сил реакций. Для трех вариантов закрепления тела выбирается тот, при котором требуемая реакция имеет наименьшее значение. Для этого варианта определяются реакции остальных опор. Определение реакций опор балки – решение задачи
Приводится решение задачи, в которой требуемая реакция опоры твердого тела определяется из одного уравнения, без определения остальных сил реакций. Для трех вариантов закрепления тела выбирается тот, при котором требуемая реакция имеет наименьшее значение. Для этого варианта определяются реакции остальных опор. Определение реакций опор балки – решение задачи Рассмотрен порядок решения задач на определение реакций опор балок. Приводится пример решения задачи двумя способами и проверка правильности определения реакций. Определение реакций опор составной конструкции – решение задачи
Рассмотрен порядок решения задач на определение реакций опор балок. Приводится пример решения задачи двумя способами и проверка правильности определения реакций. Определение реакций опор составной конструкции – решение задачи Рассмотрен метод решения задач на определение реакций опор составных конструкций для статически определимых систем. Приводится пример решения задачи, в которой требуется определить реакции в опорах и в точке соединения частей составной конструкции. Определение реакций стержней, поддерживающих прямоугольную плиту – решение задачи
Рассмотрен метод решения задач на определение реакций опор составных конструкций для статически определимых систем. Приводится пример решения задачи, в которой требуется определить реакции в опорах и в точке соединения частей составной конструкции. Определение реакций стержней, поддерживающих прямоугольную плиту – решение задачи Рассмотрены методы решения задач на равновесие с произвольной пространственной системой сил. Приводится пример решения задачи на равновесие плиты, поддерживаемой стержнями в трехмерном пространстве. Показано, как за счет выбора осей при составлении уравнений равновесия, можно упростить решение задачи.
Рассмотрены методы решения задач на равновесие с произвольной пространственной системой сил. Приводится пример решения задачи на равновесие плиты, поддерживаемой стержнями в трехмерном пространстве. Показано, как за счет выбора осей при составлении уравнений равновесия, можно упростить решение задачи. См. также: