Методы решения дифференциальных уравнений
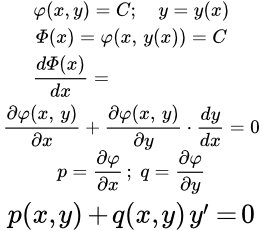
Здесь мы рассмотрим методы решения обыкновенных дифференциальных уравнений. Это уравнения, зависящие от одной независимой переменной, зависимой переменной, и ее производных:
.
Основные определения, относящиеся к дифференциальным уравнениям, изложены на странице Основные понятия и определения дифференциальных уравнений.
Мы считаем, что уравнения имеют решения в области задания переменных; Функции, заданные неявно можно разрешить относительно одной из переменной. Мы не проводим исследования этих и подобных вопросов. Здесь мы рассматриваем только методы решения.
Мы часто будем делить, и умножать уравнения на какие-то функции. В таких операциях нужно соблюдать осторожность. От этого могут появляться дополнительные решения, или исчезать имеющиеся. Например, если мы умножим все части уравнения на , то может появиться новое решение . Если мы разделим все части уравнения на , то может исчезнуть решение , если оно имелось в исходном уравнении. То есть, если мы умножаем или делим уравнение на некоторую функцию f, то всегда нужно особо рассматривать случай f = 0. Здесь мы не будем заострять на этом внимание.
Дифференциальные уравнения первого порядка
Дифференциальное уравнение и его интеграл
Далее, если это особо не оговорено, мы считаем, что x – это независимая переменная, а y – зависимая. То есть y есть функция от x: . Однако, в уравнениях первого порядка, мы можем легко менять роли переменных. То есть можно считать y независимой переменной, а x – зависимой. Но по умолчанию, x – это независимая переменная, а y – зависимая.
Пусть у нас есть дифференциальное уравнение первого порядка, разрешенное относительно производной. Запишем его в следующем виде:
(1) .
Здесь p и q – заданные функции двух переменных.
Далее рассмотрим уравнение:
(2) ,
где φ – некоторая функция двух переменных; C – постоянная, то есть число. Положим, что y есть функция от x: . Тогда будет уже сложной функцией от одной переменной x. Обозначим ее буквой : .
Перепишем уравнение (2), выразив левую часть через переменную x:
(3) .
Дифференцируем это уравнение по x, применяя правило дифференцирования сложной функции:
;
.
Мы получили дифференциальное уравнение первого порядка, имеющее тот же вид, что и уравнение (1). Отсюда следует, что если , то функция , определяемая из уравнения , является решением исходного уравнения (1).
Заметим, что левая часть уравнения является производной от функции :
.
Тогда сама функция является интегралом по отношению к уравнению (1), точнее – к его левой части. По этой причине решение уравнения, записанного в виде , называется интегралом уравнения, а сам процесс решения называется интегрированием дифференциального уравнения.
Уравнения в дифференциалах
Воспользуемся свойством дифференциалов, согласно которому
.
Перепишем уравнение (1) и умножим его на dx:
(1) ;
(4) .
Мы получили уравнение, связывающее дифференциалы переменных x и y. По этой причине такие уравнения называются дифференциальными уравнениями. Такая форма записи называется уравнением в дифференциалах, или дифференциальной формой уравнения. Уравнения (1) и (4) эквивалентны. Можно использовать любую из этих форм.
Пусть
(5) ,
где – некоторая функция двух переменных. Подставим в (4):
(6) .
Отсюда видно, что левая часть уравнения (6) является дифференциалом функции : . Тогда уравнение (6) можно переписать в виде равенства нулю дифференциала:
.
Отсюда следует, что функция равняется постоянной, которую обозначим буквой C. Тогда общий интеграл уравнения (4), при условии (5), имеет вид:
(7) .
Уравнения в полных дифференциалах
Итак, мы нашли, что если в уравнении
(4) ,
функции p и q являются частными производными
(5)
от некоторой функции φ, то уравнение (4) имеет интеграл
(7) .
Такие уравнения называются дифференциальными уравнениями в полных дифференциалах.
Как правило интеграл уравнения (7) нам не известен, а известно лишь само уравнение, то есть известны функции и . Возникает вопрос, как по известным функциям p и q определить, что левая часть уравнения является полным дифференциалом? Оказывается, что сделать это достаточно просто. Для того, чтобы уравнение было в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие:
(8) .
Доказательство
Зная, что уравнение относится к классу уравнения в полных дифференциалах, мы можем найти функцию , применяя несколько методов. Рассмотрим метод последовательного выделения дифференциала. В этом методе, мы применяем формулы дифференцирования, записанные в дифференциальной форме:
;
;
;
.
Здесь и могут быть любыми функциями от и . Рассмотрим применение этого метода на конкретном примере.
Пример
Дано уравнение:
(П1) .
Требуется проверить, является ли это уравнение в полных дифференциалах. И если является, то решить его.
Решение
В нашем случае . Проверим, является ли это уравнение в полных дифференциалах. Находим частные производные.
;
.
Видно, что . То есть это уравнение в полных дифференциалах. Решаем его, последовательно выделяя дифференциал.
.
Итак, мы нашли эквивалентное (П1) уравнение
.
Отсюда получаем его общий интеграл:
.
Решать подобные уравнения можно также и методом последовательного интегрирования. Решение этим методом можно найти на странице Дифференциальные уравнения в полных дифференциалах
Интегрирующий множитель
Итак, мы научились решать дифференциальные уравнения первого порядка
(4)
при условии
(8) .
Но если существует единственное решение уравнения (4), и условие (8) не выполняется, то оказывается, что существует такая функция , умножив на которую уравнение (4), оно становится уравнением в полных дифференциалах. Причем существует бесконечное множество таких функций. Доказательство
В качестве примера рассмотрим уравнение:
(П2) .
Перепишем его, сгруппировав члены:
.
Заметим, что . Поэтому разделим уравнение на , чтобы выделить полный дифференциал . При имеем:
.
Выделяем полный дифференциал:
;
.
Отсюда получаем общий интеграл исходного уравнения:
.
В уравнении (П2), интегрирующий множитель равен . Когда мы умножили на него уравнение, то оно стало уравнением в полных дифференциалах, которое мы и решили.
Заметим, что при умножении уравнения на множитель , мы получили другое уравнение. Оно эквивалентно исходному за исключением точек, в которых и . Уравнение корней не имеет. Поэтому этот случай отпадает. А уравнение имеет корень :
.
Поэтому умножение уравнения на множитель дает эквивалентное уравнение, за исключением точек . Другими словами, поскольку мы разделили уравнение на , то нужно проверить случай . Подстановкой в (П2) убеждаемся, что также является решением исходного уравнения. Поэтому общее решение имеет вид:
; .
Более подробно, см. Решение дифференциальных уравнений с помощью интегрирующего множителя
В этом примере мы угадали, что если уравнение умножить на , то можно выделить полный дифференциал. Не смотря на то, что для любого уравнения, при условии существования его решения, интегрирующий множитель существует, у нас нет общего метода, который позволяет найти его для любого дифференциального уравнения. Можно попытаться это сделать, но для произвольного уравнения нет гарантии, что мы найдем интегрирующий множитель, и решим уравнение. К счастью есть несколько классов уравнений, для которых это сделать можно. Эти типы уравнений мы и рассмотрим.
Уравнения с разделяющимися переменными
Рассмотрим уравнение
(9) ,
где – некоторые заданные функции. Перепишем это уравнение в дифференциалах:
.
Разделим его на . При имеем:
(11) .
Уравнение имеет вид суммы, каждое слагаемое которой зависит только от одной переменной. Говорят, что переменные разделились, а уравнение (9), по этой причине, называют дифференциальным уравнением с разделяющимися переменными.
Нетрудно видеть, что уравнение (11) в полных дифференциалах. Действительно, поскольку множитель при dx не зависит от y, то . Поскольку множитель при dy не зависит от x, то .
Видно, что необходимое и достаточное условие для полных дифференциалов выполняется:
.
Таким образом мы нашли интегрирующий множитель: . Это позволяет нам выделить дифференциал и получить решение в квадратурах:
;
;
.
Отсюда получаем общий интеграл:
.
Пример
Решить уравнение:
(П3) .
Решение
Перепишем (П3) в дифференциалах:
.
Разделим на . При имеем:
.
Переменные разделились. Общий интеграл имеет вид:
.
Далее, см. Дифференциальные уравнения с разделяющимися переменными
Уравнения, приводящиеся к разделяющимся переменным
К уравнению с разделяющимися переменными приводятся уравнения вида
,
где f – функция; a, b, c – постоянные. Для решения подобного уравнения нужно от переменной y перейти к новой переменной u, сделав подстановку .
Пример
Решить уравнение:
(П4.1)
Решение
От переменной y перейдем к переменной u. Делаем подстановку:
(П4.2) .
Здесь и – функции от x. Дифференцируем (П4.2) по x, и подставляем (П4.1):
;
.
Тем самым мы получили дифференциальное уравнение с разделяющимися переменными.
См. далее Дифференциальные уравнения, приводящиеся к уравнениям с разделяющимися переменными
Однородные уравнения
Однородные дифференциальные уравнения первого порядка имеют вид
.
Чтобы определить, является ли уравнение однородным, нужно сделать замену . Здесь t – постоянная. Если t сократится, то это однородное уравнение. Для его решения нужно от переменной y перейти к переменной u, сделав подстановку . После этого, уравнение сводится к уравнению с разделяющимися переменными.
Пример
(П5) .
Решение
Проверим, является ли это уравнение однородным. Сделаем замену . Считаем, что постоянная :
;
;
.
Постоянная t сократилась. Она также сократится, если считать . Это однородное уравнение. Переходим от переменной y к переменной u. Для этого делаем подстановку , где u – функция от x. Дифференцируем по x:
.
Подставляем в(П5):
;
;
.
При , берем знак ′+′. При – знак ′–′. Мы получили уравнение с разделяющимися переменными, решать которое мы уже умеем.
Далее см. Однородные дифференциальные уравнения первого порядка
Уравнения, приводящиеся к однородным
Уравнение вида
.
приводится к однородному подстановками
,
где – новые переменные; – постоянные, которые выбираются из условий
.
Пример
(П6) .
Решение
От переменных x и y, переходим к переменным t и u. Делаем подстановку . Тогда ;
;
;
.
Решаем систему из двух линейных уравнений
Определив и , получаем однородное уравнение:
.
Метод решения такого уравнения мы только что рассмотрели. См. Дифференциальные уравнения первого порядка, приводящиеся к однородным
Обобщенные однородные уравнения
К однородным уравнениям приводятся уравнения вида
.
Чтобы определить, является ли дифференциальное уравнение обобщенным однородным, нужно ввести постоянную t и сделать замену: . Если удастся выбрать такое значение α, при котором постоянная t сократится, то это – обобщенное однородное дифференциальное уравнение. Для решения этого уравнения, нужно от переменной y перейти к переменной u, сделав подстановку . При этом уравнение сводится к разделяющимся переменным.
Пример
(П7) .
Решение
Проверим, является ли уравнение (П7) обобщенным однородным. Делаем замену: .
.
Подставляем в (П7):
.
Делим на :
.
Отсюда видно, что t сокращается, если положить .
Итак, мы нашли, что это обобщенное однородное уравнение с . Решаем его. От переменной y переходим к переменной u, выполняя подстановку .
;
;
.
Подставляем в (П7):
(П7) ;
;
;
;
.
Мы получили уравнение с разделяющимися переменными.
См. далее Обобщенные однородные дифференциальные уравнения первого порядка
Линейные уравнения
Дифференциальные уравнения, вида
(11)
называются линейными дифференциальными уравнениями первого порядка.
Решение с помощью интегрирующего множителя
Уравнение (11) имеет интегрирующий множитель .
См. Решение линейных дифференциальных уравнений первого порядка
Продемонстрируем это на примере.
Пример
(П8.1) .
Решение
Это линейное уравнение первого порядка. Решаем его с помощью интегрирующего множителя. Разделим (П8.1) на x:
(П8.2) .
Тогда . Находим интегрирующий множитель :
; .
Пусть . Тогда . Умножаем (П8.2) на и выделяем полный дифференциал:
;
;
;
.
Отсюда , или .
Мы нашли интегрирующий множитель полагая, что . После умножения на него, мы получили уравнение в полных дифференциалах как при , так и при . При решении мы нигде не полагали, что . Это предположение нам потребовалось, только чтобы выбрать интегрирующий множитель. На самом деле, любое уравнение первого порядка имеет бесконечное число интегрирующих множителей. Поэтому, если бы мы в самом начале взяли , то получили бы множитель . И с его помощью, получили то же самое решение.
Решение методом Бернулли
Линейное уравнение первого порядка можно решить красивым приемом, введя две функции и , зависящие от переменной x. Сделаем подстановку . Тогда . Подставим в исходное уравнение (11):
(11) ;
;
(12) .
Наложим условие
(13) .
Уравнение (13) с разделяющимися переменными. Решаем его, и возьмем любое, отличное от нуля частное решение. Так мы определим функцию . Учитывая (13), уравнение (12) примет вид:
.
Теперь здесь уже известная функция, и это уравнение с разделяющимися переменными. Решая его, найдем общее решение . Вместе с этим получаем общее решение исходного уравнения (11): .
Подробнее, см. Решение линейного ДУ первого порядка методом Бернулли
Решение методом Лагранжа
Метод Лагранжа интересен тем, что указывает путь поиска решения от простого к сложному. Рассмотрим линейное уравнение:
(11) .
Давайте его упростим. Сначала рассмотрим однородное уравнение – то есть уравнение с :
(14) .
Это уравнение с разделяющимися переменными, и мы можем его решить:
;
;
;
;
.
Заменим постоянную на C. Тогда общее решение примет вид:
(15) , где .
Теперь вернемся к исходному неоднородному уравнению (11). Попытаемся найти его решение, используя решение более простого, однородного уравнения (14). Для этого в (15) заменим постоянную C на функцию, зависящую от переменной x: . То есть будем искать решение в виде
.
Подставляя в (11), получим для дифференциальное уравнение с разделяющимися переменными, которое решается в квадратурах. Решив его, получаем решение исходного уравнения. Такой метод решения называется методом вариации постоянных, или методом Лагранжа.
См. Решение линейных ДУ первого порядка методом Лагранжа
Дифференциальное уравнение Бернулли
Дифференциальное уравнение Бернулли имеет вид:
,
где и – заданные функции от x. Можно убедиться, что оно сводится к линейному уравнению подстановкой .
См. Дифференциальное уравнение Бернулли и методы его решения
Однако его легче решать методом двух функций Бернулли. Для этого вводим две функции и . Ищем решение в виде . Одну из этих функций выбираем так, чтобы уравнение для другой функции превратилось в уравнение с разделяющимися переменными.
Пример
(П9.1)
Решение
Это уравнение Бернулли. Решаем методом Бернулли. Ищем решение в виде произведения двух функций: . Тогда
. Подставляем в (П9.1):
;
(П9.2) .
Одну из этих функций мы можем выбрать произвольным образом. Выберем v так, чтобы выражение в круглых скобках равнялось нулю:
(П9.3) .
Тогда уравнение (П9.2) превратится в уравнение с разделяющимися переменными.
Решаем уравнение (П9.3). Разделяем переменные.
;
;
;
;
.
Возьмем решение , или .
Подставим в (П9.2), учитывая (П9.3), и разделяем переменные:
(П9.2) ;
;
;
.
При имеем:
;
;
;
;
;
.
Заменим постоянную интегрирования: . Тогда решение уравнения (П9.1) примет вид:
.
Теперь рассмотрим случай . Нетрудно увидеть, что это также решение уравнения (П9.2). Тогда является решением исходного уравнения. Получаем общее решение исходного уравнения:
.
Уравнения, не разрешенные относительно производной
Существует несколько типов уравнений, не разрешенных относительно производной, которые допускают решение. При этом они должны быть разрешены относительно одной из переменной. Далее перечислены типы этих уравнений, и даны ссылки на страницы с методами их решений.
уравнение, содержащее только производную
;
уравнения, не содержащие одну из переменных
уравнение Клеро
уравнение Лагранжа
;
приводящиеся к уравнению Бернулли
Дифференциальные уравнения второго и высших порядков
Уравнения, допускающие понижение порядка
Уравнения, не содержащие y в явном виде
Рассмотрим уравнения вида
.
Если сделать подстановку , то . То есть мы понизили на единицу порядок такого уравнения.
См. Дифференциальные уравнения, не содержащие функцию в явном виде
Уравнения, не содержащие x в явном виде
Рассмотрим уравнения, которые не содержат независимую переменную x в явном виде:
.
Мы можем понизить порядок таких уравнений, если от переменных x и y перейдем к независимой переменной y и зависимой переменной y′. То есть, считаем, что все производные являются функциями от y.
Пример
(П10.1)
Решение
Это уравнение не содержит независимую переменную x в явном виде. Переходим к новым переменным. Пусть независимой переменной является y, а зависимой y′. Введем для нее обозначение:
. Тогда по правилу дифференцирования сложной функции, имеем:
.
Подставляем в (П10.1):
.
Мы получили дифференциальное уравнение первого порядка с разделяющимися переменными.
Далее, см. Дифференциальные уравнения высших порядков, не содержащие переменную в явном виде
Уравнения, однородные относительно функции и ее производных
Это уравнения вида
.
Чтобы распознать такое уравнение, нужно сделать замены , и т.д. Если постоянная t сократится, то это уравнение однородное относительно функции и ее производных.
Для решения, мы от зависимой переменной y переходим к новой зависимой переменной u с помощью подстановки
,
где – функция от x.
Пример
(П11.1)
Решение
Проверим, является ли это уравнение однородным относительно функции и ее производных. Заменим в исходном уравнении y на ty, y′ на ty′, y′′ на ty′′:
;
.
Постоянная t сокращается. Значит это уравнение однородное относительно функции и ее производных.
Делаем подстановку , где – функция от x.
.
(П11.1) ;
.
Делим на . При имеем:
;
;
.
Мы получили линейное дифференциальное уравнение первого порядка. См. далее ДУ высших порядков, однородные относительно функции и ее производных
Линейные уравнения с постоянными коэффициентами
В линейных уравнениях с постоянными коэффициентами, допускающими решение в аналитическом виде, можно сделать линейную подстановку, и понизить порядок уравнения. Однако проще воспользоваться свойствами линейных уравнений и решать их более простым методом.
Общие свойства линейных уравнений
Рассмотрим линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами:
(Л1) ,
где – постоянные, то есть не зависящие от переменной x коэффициенты (числа). При этом . Это уравнение имеет n линейно независимых решений:
(Л2) .
Они называются фундаментальной системой решений. Когда n линейно независимых решений найдены, то общее решение однородного уравнения (Л1) имеет вид:
.
Теперь рассмотрим более общее – линейное неоднородное дифференциальное уравнение n-го порядка с постоянными коэффициентами:
(Л3) ,
где – непрерывная функция на некотором отрезке . Тогда, на этом отрезке, уравнение (Л3) имеет решение, удовлетворяющее заданным начальным условиям:
, где – любые действительные числа; .
Пусть есть частное (любое) решение уравнения (Л3). Тогда общее решение неоднородного уравнения (Л3) равно сумме частного решения неоднородного уравнения, и общего решения однородного:
,
где – общее решение однородного уравнения (Л1).
Если, в уравнении (Л3), неоднородную часть можно представить в виде суммы p слагаемых:
,
то частное решение равно сумме отдельных частных решений: . Здесь – частное решение уравнения
.
См. Определение и основные свойства линейных дифференциальных уравнений с постоянными коэффициентами
Решение однородного уравнения
Рассмотрим линейное однородное ДУ n-го порядка с постоянными коэффициентами:
(Л1) .
Чтобы найти его общее решение, нам нужно найти n линейно независимых решений. Или, как говорят, найти фундаментальную систему решений. Ищем решение в виде . Подставляя в (Л1), получаем уравнение степени n, которое называют характеристическим уравнением:
(Л4) .
Оно имеет n корней , и может быть записано в виде:
.
Каждому корню соответствует частное решение, входящее в состав фундаментальной системы. При этом корни могут быть кратными и комплексными. Рассмотрим правила составления линейно независимых решений.
Действительному единственному корню соответствует решение .
Действительному корню кратности p, соответствуют p линейно независимых решений:
.
Если есть единственный комплексный корень , то имеется и комплексно сопряженный корень . Им соответствуют два линейно независимых решения
.
Если есть кратный комплексный корень кратности p, то имеется и комплексно сопряженный корень, кратности p: . Им соответствуют 2p линейно независимых решений
;
;
;
............
.
Более подробно, см. Решение линейных однородных дифференциальных уравнений с постоянными коэффициентами
Пример
(П12.1)
Решение
Ищем решение в виде . Составляем характеристическое уравнение и преобразуем его:
;
(П12.2) .
Решаем квадратное уравнение :
.
Перепишем характеристическое уравнение (П12.2) в эквивалентном виде:
.
Корням кратности 2 соответствуют два линейно независимых решения:
;
.
Комплексно сопряженным корням , соответствуют решения
.
Общее решение:
.
Решение уравнений со специальной неоднородностью
Рассмотрим, часто встречающееся в приложениях, линейное неоднородное уравнение с постоянными коэффициентами со специальной неоднородностью:
(Л5.1) ,
где правая часть представлена в виде произведений степенной функции, экспоненты, косинусов и синусов:
(Л5.2) .
Здесь – многочлены степеней и , соответственно.
Общее решение (Л5.1) – (Л5.2) имеет вид:
.
Здесь – общее решение однородного уравнения (с ); – частное решение неоднородного уравнения (Л5.1)–(Л5.2). Как найти общее решение , мы рассмотрели в предыдущем пункте. Изложим метод нахождения частного решения.
Ищем методом неопределенных коэффициентов. Известно, что для уравнения (Л5.1) – (Л5.2), частное решение имеет следующий вид:
(Л6) .
Здесь ; и – многочлены степени s. Если среди корней характеристического уравнения (Л4) ⇑ нет корня , то . Если такой корень есть, то m – его кратность.
Метод нахождения частного решения заключается в том, что мы ищем решение в виде (Л6). Для этого записываем многочлены в общем виде:
;
.
Здесь коэффициенты (числа), которые нужно определить. Далее мы выписываем (Л6) в общем виде:
.
Находим n производных , и подставляем их выражения в исходное уравнение (Л5.1) – (Л5.2). В левой части мы получим сумму из членов с множителями , и членов с множителями . Здесь . В правой, неоднородной части, также имеется членов с множителями , и членов с множителями . При этом часть из них может равняться нулю. Приравнивая коэффициенты при этих множителях, получим систему из уравнений, решая которую, мы определяем неизвестные коэффициенты .
Если , то правая часть имеет более простой вид:
(Л5.3) .
Тогда частное решение содержит неопределенных коэффициентов:
.
Здесь , если характеристическое уравнение (Л4) ⇑ не имеет действительного корня . Если характеристическое уравнение имеет действительный корень , то m – его кратность.
Далее находим выражения для n производных , и подставляем их в исходное уравнение (Л4.1) – (Л4.2). В левой части мы получим сумму из членов с множителями . В правой, неоднородной части, также имеется членов с множителями . Часть из них может равняться нулю. Приравнивая коэффициенты при этих множителях, получим систему из уравнений, решая которую, мы определяем неизвестные коэффициенты .
Наконец, если и , и , то
(Л5.4) .
Частное решение, как и в предыдущем случае, имеет неопределенных коэффициентов:
.
Если характеристическое уравнение не имеет действительного корня , то . Если характеристическое уравнение имеет такой корень, то m – его кратность. Находим выражения для n производных ; подставляем их в исходное уравнение (Л4.1) – (Л4.2). В левой части мы получим сумму из членов с множителями . В правой, неоднородной части, также имеется членов с множителями . Часть из них может равняться нулю. Приравнивая коэффициенты при этих множителях, получим систему из уравнений, решая которую, определяем неизвестные коэффициенты .
См. Пример решения линейного ДУ с постоянными коэффициентами со специальной неоднородной частью
Решение неоднородных уравнений общего вида
Теперь рассмотрим методы решения линейного неоднородного ДУ n-го порядка с постоянными коэффициентами с неоднородностью общего вида:
(Л3) .
В отличие от предыдущего случая со специальной неоднородностью, в этом разделе мы считаем, что неоднородность имеет произвольный вид.
Решение методом Бернулли
Метод Бернулли заключается в том, что мы ищем решение уравнения
(Л3)
в виде произведения двух функций и , зависящих от переменной x:
.
Если в качестве v взять частное решение однородного уравнения
,
то такая подстановка приводит к понижению порядка исходного уравнения (Л3).
Пример
(П13.1)
Решение
Ищем решение в виде произведения двух функций; подставляем в уравнение (П13.1) и группируем члены:
(П13.2) ;
;
.
(П13.1) ;
;
(П13.3) ;
Решаем однородное уравнение
(П13.4) .
Ищем решение в виде . Составляем и решаем характеристическое уравнение:
;
.
Получаем два кратных корня . Общее решение уравнения (П13.4):
.
В качестве v мы можем взять любое, отличное от нуля решение. Поэтому положим
. Тогда ; .
Подставим в (П13.3), учитывая (П13.4):
;
;
;
;
;
.
См. также Решение ДУ высших порядков методом Бернулли
Понижение порядка линейной подстановкой
Порядок линейного уравнения с постоянными коэффициентами можно понизить с помощью подстановки . Более подробно этот материал изложен на странице «Понижение порядка в линейных неоднородных ДУ с постоянными коэффициентами». Здесь мы рассмотрим пример применения этого метода.
Пример
Решить уравнение, применяя линейную подстановку
(П14.1)
Решение
Перепишем левую часть уравнения (П14.1), введя оператор дифференцирования :
.
Подставим в (П14.1). Исходное уравнение принимает вид
.
Сделаем подстановку . В результате для переменной u получаем уравнение первого порядка:
;
.
Итак, подстановкой
(П14.2) ,
мы получили уравнение первого порядка:
(П14.3) .
Решаем уравнение (П14.3), умножая его на интегрирующий множитель :
;
;
;
;
.
Подставляем в уравнение (П14.2) и решаем его с помощью интегрирующего множителя .
;
;
;
;
;
.
Более подробно, см. Понижение порядка в линейных неоднородных ДУ с постоянными коэффициентами
Метод вариации постоянных Лагранжа
Выпишем еще раз линейное неоднородного ДУ n-го порядка с постоянными коэффициентами:
(Л3) .
Метод вариации постоянных, который мы применили для уравнения первого поряддка, также применим и для уравнений произвольного порядка.
Для решения уравнения (Л3), мы вначале решаем однородное уравнение
.
Получаем его общее решение, которое имеет вид:
(Л7) .
Далее мы считаем, что постоянные являются функциями от x. То есть заменяем постоянные на некоторые, пока не известные, функции . Подставляем в (Л7), и ищем решение исходного уравнения (Л3) в следующем виде:
(Л8) .
Подставляем (Л8) в (Л3). При этом на функции накладываем дополнительные ограничения:
.
В результате получаем систему n линейных уравнений относительно неизвестных . Решая эту систему, получаем значения производных , как функций от x. Интегрируя, получаем выражения для самих функций . Подставляя в (Л8), получаем общее решение исходного уравнения (Л3).
Более подробно, см. Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа
Уравнение Эйлера
Уравнение
(Л9)
называется дифференциальным уравнением Эйлера. Подстановкой
(Л10)
оно приводится к уравнению с постоянными коэффициентами.
В некоторых случаях, уравнение Эйлера проще решать напрямую, не прибегая к подстановке (Л10). При решении неоднородного уравнения, к уравнению Эйлера применимы методы двух функций Бернулли, и метод вариации постоянных Лагранжа.
Рассмотрим однородное уравнение Эйлера:
(Л11) .
Его тоже проще решить без подстановки (Л10). Для этого мы ищем решение в виде . Находим производные, и подставляем в уравнение (Л11). В результате получаем характеристическое уравнение степени n. Оно имеет n корней.
Действительному корню , кратности p, соответствуют p линейно независимых решений
;
.
Если есть комплексный корень кратности p, то есть и комплексно сопряженный корень кратности p. Им соответствуют линейно независимых решений
;
;
.................
.
Определив фундаментальную систему решений , получаем общее решение однородного уравнения (Л11):
.
Более подробно, см. Дифференциальное уравнение Эйлера и методы его решения
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Л.Э. Эльсгольц, Дифференциальные уравнения и вариационное исчисление, М., 1969.
Автор: Олег Одинцов. Опубликовано:
