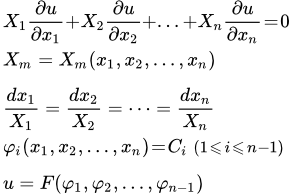Методы решения дифференциальных уравнений в картинках

Приводятся основные сведения об обыкновенных дифференциальных уравнениях в сжатом виде – в картинках. Большинство из них содержат методы решения уравнений.
Содержание
См. также:
Здесь приводятся главные картинки страниц раздела «Дифференциальные уравнения». На этих изображениях, в кратком виде представлены главные содержания страниц раздела. В частности, на многих из них даются методы решения уравнений. Просматривая картинки, можно освежить в памяти методы решений дифференциальных уравнений. Также каждый заголовок снабжен ссылкой на страницу, к которой относится картинка.
Дифференциальные уравнения первого порядка
Методы решения дифференциальных уравнений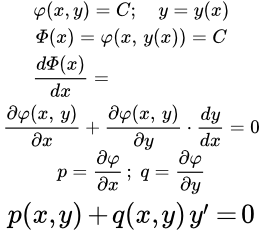 Рассмотрены основные методы решения обыкновенных дифференциальных уравнений с примерами их решений. Рассмотрены уравнения в полных дифференциалах, интегрирующий множитель, уравнения с разделяющимися переменными, однородные, линейные, уравнения Бернулли, уравнения второго и высших порядков. Даны три метода решений линейных уравнений с постоянными коэффициентами. Основные понятия и определения дифференциальных уравнений
Рассмотрены основные методы решения обыкновенных дифференциальных уравнений с примерами их решений. Рассмотрены уравнения в полных дифференциалах, интегрирующий множитель, уравнения с разделяющимися переменными, однородные, линейные, уравнения Бернулли, уравнения второго и высших порядков. Даны три метода решений линейных уравнений с постоянными коэффициентами. Основные понятия и определения дифференциальных уравнений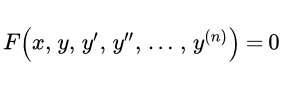 Рассмотрены основные понятия и определения обыкновенных дифференциальных уравнений и их решений. Дифференциальные уравнения первого порядка
Рассмотрены основные понятия и определения обыкновенных дифференциальных уравнений и их решений. Дифференциальные уравнения первого порядка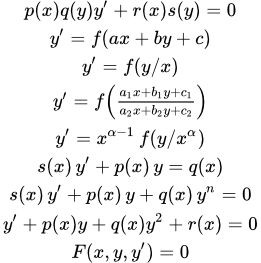 Приведена инструкция, как решать дифференциальные уравнения первого порядка. Перечислены основные типы обыкновенных ДУ первого порядка. Кратко изложены методы их решения. Указаны ссылки на страницы с подробным изложением методов решения и разобранными примерами. Дифференциальные уравнения с разделяющимися переменными
Приведена инструкция, как решать дифференциальные уравнения первого порядка. Перечислены основные типы обыкновенных ДУ первого порядка. Кратко изложены методы их решения. Указаны ссылки на страницы с подробным изложением методов решения и разобранными примерами. Дифференциальные уравнения с разделяющимися переменными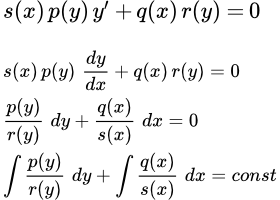 Рассмотрен метод решения дифференциальных уравнений с разделяющимися переменными. Дан пример подробного решения дифференциального уравнения с разделяющимися переменными. Дифференциальные уравнения, приводящиеся к уравнениям с разделяющимися переменными
Рассмотрен метод решения дифференциальных уравнений с разделяющимися переменными. Дан пример подробного решения дифференциального уравнения с разделяющимися переменными. Дифференциальные уравнения, приводящиеся к уравнениям с разделяющимися переменными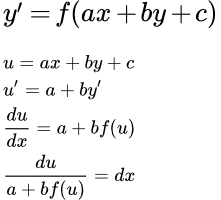 Рассмотрен способ решения дифференциальных уравнений, приводящихся к уравнениям с разделяющимися переменными. Дан пример подробного решения дифференциального уравнения, приводящегося к уравнению с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка
Рассмотрен способ решения дифференциальных уравнений, приводящихся к уравнениям с разделяющимися переменными. Дан пример подробного решения дифференциального уравнения, приводящегося к уравнению с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка Показано как определить, что дифференциальное уравнение первого порядка является однородным. Рассмотрены методы решений однородных дифференциальных уравнений первого порядка. Дан пример подробного решения однородного дифференциального уравнения. Дифференциальные уравнения первого порядка, приводящиеся к однородным
Показано как определить, что дифференциальное уравнение первого порядка является однородным. Рассмотрены методы решений однородных дифференциальных уравнений первого порядка. Дан пример подробного решения однородного дифференциального уравнения. Дифференциальные уравнения первого порядка, приводящиеся к однородным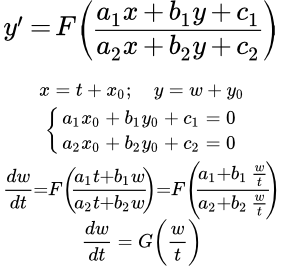 Рассмотрен метод решения дифференциальных уравнений, приводящихся к однородным дифференциальным уравнениям первого порядка. Дан пример подробного решения дифференциального уравнения, приводящегося к однородному уравнению. Обобщенные однородные дифференциальные уравнения первого порядка
Рассмотрен метод решения дифференциальных уравнений, приводящихся к однородным дифференциальным уравнениям первого порядка. Дан пример подробного решения дифференциального уравнения, приводящегося к однородному уравнению. Обобщенные однородные дифференциальные уравнения первого порядка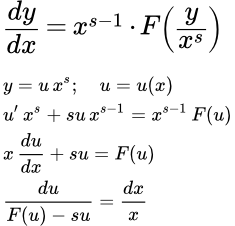 Показано как распознать и решить обобщенное однородное дифференциальное уравнение первого порядка. Рассмотрен пример подробного решения такого уравнения. Решение линейных дифференциальных уравнений первого порядка
Показано как распознать и решить обобщенное однородное дифференциальное уравнение первого порядка. Рассмотрен пример подробного решения такого уравнения. Решение линейных дифференциальных уравнений первого порядка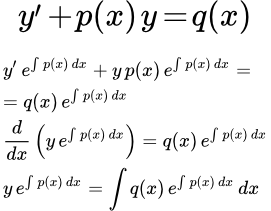 Определение линейного дифференциального уравнения первого порядка. Рассмотрен метод решения линейных дифференциальных уравнений первого порядка с помощью интегрирующего множителя. Дан пример подробного решения такого уравнения. Метод Бернулли (введение двух функций). Линейные дифференциальные уравнения первого порядка
Определение линейного дифференциального уравнения первого порядка. Рассмотрен метод решения линейных дифференциальных уравнений первого порядка с помощью интегрирующего множителя. Дан пример подробного решения такого уравнения. Метод Бернулли (введение двух функций). Линейные дифференциальные уравнения первого порядка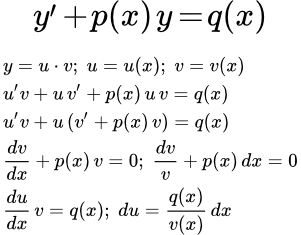 Изложен способ решения линейных дифференциальных уравнений первого порядка методом Бернулли – введением двух функций. Рассмотрен пример подробного решения линейного дифференциального уравнения методом Бернулли. Метод Лагранжа (вариации постоянной). Линейные дифференциальные уравнения первого порядка.
Изложен способ решения линейных дифференциальных уравнений первого порядка методом Бернулли – введением двух функций. Рассмотрен пример подробного решения линейного дифференциального уравнения методом Бернулли. Метод Лагранжа (вариации постоянной). Линейные дифференциальные уравнения первого порядка.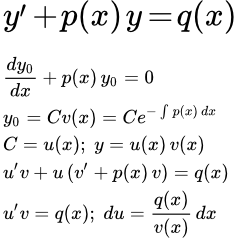 Рассмотрен способ решения линейных дифференциальных уравнений первого порядка методом вариации постоянной (Лагранжа). Дан пример подробного решения линейного дифференциального уравнения методом Лагранжа. Дифференциальные уравнения первого порядка, приводящиеся к линейным
Рассмотрен способ решения линейных дифференциальных уравнений первого порядка методом вариации постоянной (Лагранжа). Дан пример подробного решения линейного дифференциального уравнения методом Лагранжа. Дифференциальные уравнения первого порядка, приводящиеся к линейным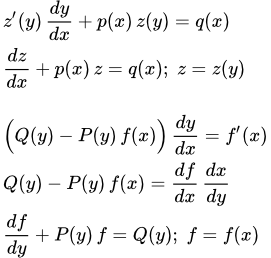 Рассмотрены дифференциальные уравнения, приводящиеся к линейным дифференциальным уравнениям первого порядка. Дан пример подробного решения дифференциального уравнения, приводящегося к линейному уравнению. Дифференциальное уравнение Бернулли и методы его решения
Рассмотрены дифференциальные уравнения, приводящиеся к линейным дифференциальным уравнениям первого порядка. Дан пример подробного решения дифференциального уравнения, приводящегося к линейному уравнению. Дифференциальное уравнение Бернулли и методы его решения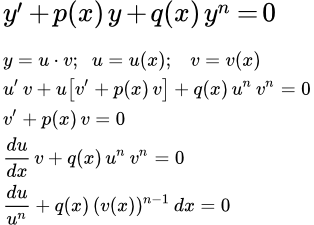 Дано определение дифференциального уравнения Бернулли. Рассмотрены методы его решения: приведением к линейному уравнению и методом Бернулли. Рассмотрены два примера уравнений с подробными решениями методом Бернулли. Дифференциальное уравнение Риккати
Дано определение дифференциального уравнения Бернулли. Рассмотрены методы его решения: приведением к линейному уравнению и методом Бернулли. Рассмотрены два примера уравнений с подробными решениями методом Бернулли. Дифференциальное уравнение Риккати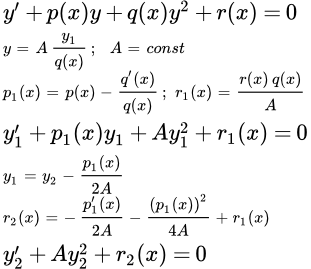 Дано определение дифференциального уравнения Риккати. Рассмотрены его свойства, приведение к более простой форме и частные случаи решения. Дифференциальное уравнение Якоби
Дано определение дифференциального уравнения Риккати. Рассмотрены его свойства, приведение к более простой форме и частные случаи решения. Дифференциальное уравнение Якоби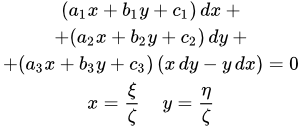 Дано определение дифференциального уравнения Якоби и рассмотрен метод его решения. Дифференциальные уравнения в полных дифференциалах
Дано определение дифференциального уравнения Якоби и рассмотрен метод его решения. Дифференциальные уравнения в полных дифференциалах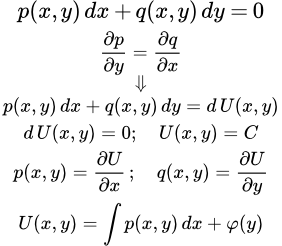 Показано как распознать дифференциальное уравнение в полных дифференциалах. Даны методы его решения. Приводится пример решения уравнения в полных дифференциалах двумя способами. Решение дифференциальных уравнений с помощью интегрирующего множителя
Показано как распознать дифференциальное уравнение в полных дифференциалах. Даны методы его решения. Приводится пример решения уравнения в полных дифференциалах двумя способами. Решение дифференциальных уравнений с помощью интегрирующего множителя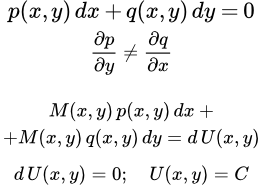 Рассмотрен метод решения дифференциальных уравнений первого порядка с помощью интегрирующего множителя. Приведены свойства интегрирующих множителей и указаны методы их нахождения. Разобраны примеры решений уравнений с помощью интегрирующего множителя. Теорема Коши существования и единственности решения дифференциального уравнения первого порядка
Рассмотрен метод решения дифференциальных уравнений первого порядка с помощью интегрирующего множителя. Приведены свойства интегрирующих множителей и указаны методы их нахождения. Разобраны примеры решений уравнений с помощью интегрирующего множителя. Теорема Коши существования и единственности решения дифференциального уравнения первого порядка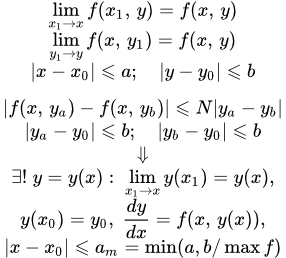 Формулировка теоремы Коши существования и единственности решения дифференциального уравнения первого порядка. Доказательство теоремы методом последовательных приближений Пикара.
Формулировка теоремы Коши существования и единственности решения дифференциального уравнения первого порядка. Доказательство теоремы методом последовательных приближений Пикара.
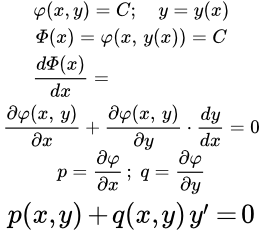 Рассмотрены основные методы решения обыкновенных дифференциальных уравнений с примерами их решений. Рассмотрены уравнения в полных дифференциалах, интегрирующий множитель, уравнения с разделяющимися переменными, однородные, линейные, уравнения Бернулли, уравнения второго и высших порядков. Даны три метода решений линейных уравнений с постоянными коэффициентами. Основные понятия и определения дифференциальных уравнений
Рассмотрены основные методы решения обыкновенных дифференциальных уравнений с примерами их решений. Рассмотрены уравнения в полных дифференциалах, интегрирующий множитель, уравнения с разделяющимися переменными, однородные, линейные, уравнения Бернулли, уравнения второго и высших порядков. Даны три метода решений линейных уравнений с постоянными коэффициентами. Основные понятия и определения дифференциальных уравнений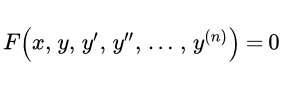 Рассмотрены основные понятия и определения обыкновенных дифференциальных уравнений и их решений. Дифференциальные уравнения первого порядка
Рассмотрены основные понятия и определения обыкновенных дифференциальных уравнений и их решений. Дифференциальные уравнения первого порядка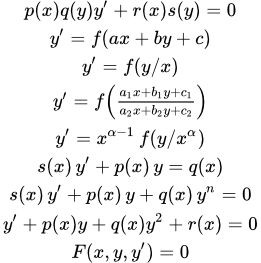 Приведена инструкция, как решать дифференциальные уравнения первого порядка. Перечислены основные типы обыкновенных ДУ первого порядка. Кратко изложены методы их решения. Указаны ссылки на страницы с подробным изложением методов решения и разобранными примерами. Дифференциальные уравнения с разделяющимися переменными
Приведена инструкция, как решать дифференциальные уравнения первого порядка. Перечислены основные типы обыкновенных ДУ первого порядка. Кратко изложены методы их решения. Указаны ссылки на страницы с подробным изложением методов решения и разобранными примерами. Дифференциальные уравнения с разделяющимися переменными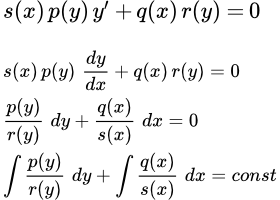 Рассмотрен метод решения дифференциальных уравнений с разделяющимися переменными. Дан пример подробного решения дифференциального уравнения с разделяющимися переменными. Дифференциальные уравнения, приводящиеся к уравнениям с разделяющимися переменными
Рассмотрен метод решения дифференциальных уравнений с разделяющимися переменными. Дан пример подробного решения дифференциального уравнения с разделяющимися переменными. Дифференциальные уравнения, приводящиеся к уравнениям с разделяющимися переменными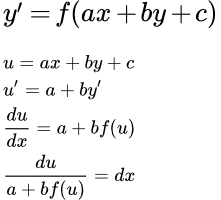 Рассмотрен способ решения дифференциальных уравнений, приводящихся к уравнениям с разделяющимися переменными. Дан пример подробного решения дифференциального уравнения, приводящегося к уравнению с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка
Рассмотрен способ решения дифференциальных уравнений, приводящихся к уравнениям с разделяющимися переменными. Дан пример подробного решения дифференциального уравнения, приводящегося к уравнению с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка Показано как определить, что дифференциальное уравнение первого порядка является однородным. Рассмотрены методы решений однородных дифференциальных уравнений первого порядка. Дан пример подробного решения однородного дифференциального уравнения. Дифференциальные уравнения первого порядка, приводящиеся к однородным
Показано как определить, что дифференциальное уравнение первого порядка является однородным. Рассмотрены методы решений однородных дифференциальных уравнений первого порядка. Дан пример подробного решения однородного дифференциального уравнения. Дифференциальные уравнения первого порядка, приводящиеся к однородным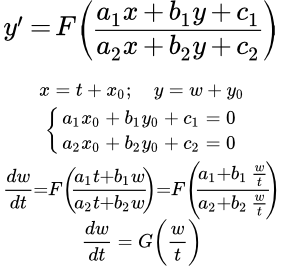 Рассмотрен метод решения дифференциальных уравнений, приводящихся к однородным дифференциальным уравнениям первого порядка. Дан пример подробного решения дифференциального уравнения, приводящегося к однородному уравнению. Обобщенные однородные дифференциальные уравнения первого порядка
Рассмотрен метод решения дифференциальных уравнений, приводящихся к однородным дифференциальным уравнениям первого порядка. Дан пример подробного решения дифференциального уравнения, приводящегося к однородному уравнению. Обобщенные однородные дифференциальные уравнения первого порядка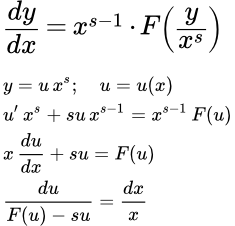 Показано как распознать и решить обобщенное однородное дифференциальное уравнение первого порядка. Рассмотрен пример подробного решения такого уравнения. Решение линейных дифференциальных уравнений первого порядка
Показано как распознать и решить обобщенное однородное дифференциальное уравнение первого порядка. Рассмотрен пример подробного решения такого уравнения. Решение линейных дифференциальных уравнений первого порядка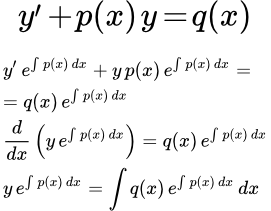 Определение линейного дифференциального уравнения первого порядка. Рассмотрен метод решения линейных дифференциальных уравнений первого порядка с помощью интегрирующего множителя. Дан пример подробного решения такого уравнения. Метод Бернулли (введение двух функций). Линейные дифференциальные уравнения первого порядка
Определение линейного дифференциального уравнения первого порядка. Рассмотрен метод решения линейных дифференциальных уравнений первого порядка с помощью интегрирующего множителя. Дан пример подробного решения такого уравнения. Метод Бернулли (введение двух функций). Линейные дифференциальные уравнения первого порядка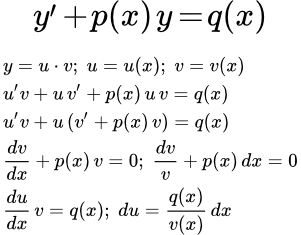 Изложен способ решения линейных дифференциальных уравнений первого порядка методом Бернулли – введением двух функций. Рассмотрен пример подробного решения линейного дифференциального уравнения методом Бернулли. Метод Лагранжа (вариации постоянной). Линейные дифференциальные уравнения первого порядка.
Изложен способ решения линейных дифференциальных уравнений первого порядка методом Бернулли – введением двух функций. Рассмотрен пример подробного решения линейного дифференциального уравнения методом Бернулли. Метод Лагранжа (вариации постоянной). Линейные дифференциальные уравнения первого порядка.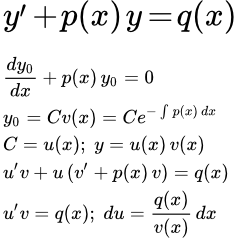 Рассмотрен способ решения линейных дифференциальных уравнений первого порядка методом вариации постоянной (Лагранжа). Дан пример подробного решения линейного дифференциального уравнения методом Лагранжа. Дифференциальные уравнения первого порядка, приводящиеся к линейным
Рассмотрен способ решения линейных дифференциальных уравнений первого порядка методом вариации постоянной (Лагранжа). Дан пример подробного решения линейного дифференциального уравнения методом Лагранжа. Дифференциальные уравнения первого порядка, приводящиеся к линейным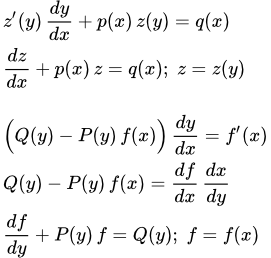 Рассмотрены дифференциальные уравнения, приводящиеся к линейным дифференциальным уравнениям первого порядка. Дан пример подробного решения дифференциального уравнения, приводящегося к линейному уравнению. Дифференциальное уравнение Бернулли и методы его решения
Рассмотрены дифференциальные уравнения, приводящиеся к линейным дифференциальным уравнениям первого порядка. Дан пример подробного решения дифференциального уравнения, приводящегося к линейному уравнению. Дифференциальное уравнение Бернулли и методы его решения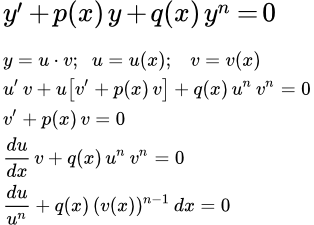 Дано определение дифференциального уравнения Бернулли. Рассмотрены методы его решения: приведением к линейному уравнению и методом Бернулли. Рассмотрены два примера уравнений с подробными решениями методом Бернулли. Дифференциальное уравнение Риккати
Дано определение дифференциального уравнения Бернулли. Рассмотрены методы его решения: приведением к линейному уравнению и методом Бернулли. Рассмотрены два примера уравнений с подробными решениями методом Бернулли. Дифференциальное уравнение Риккати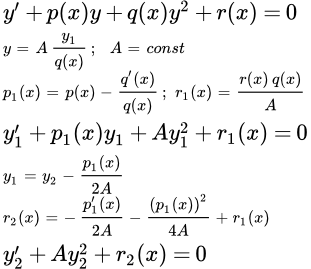 Дано определение дифференциального уравнения Риккати. Рассмотрены его свойства, приведение к более простой форме и частные случаи решения. Дифференциальное уравнение Якоби
Дано определение дифференциального уравнения Риккати. Рассмотрены его свойства, приведение к более простой форме и частные случаи решения. Дифференциальное уравнение Якоби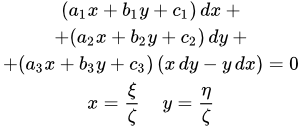 Дано определение дифференциального уравнения Якоби и рассмотрен метод его решения. Дифференциальные уравнения в полных дифференциалах
Дано определение дифференциального уравнения Якоби и рассмотрен метод его решения. Дифференциальные уравнения в полных дифференциалах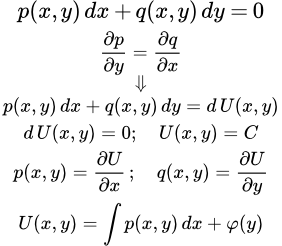 Показано как распознать дифференциальное уравнение в полных дифференциалах. Даны методы его решения. Приводится пример решения уравнения в полных дифференциалах двумя способами. Решение дифференциальных уравнений с помощью интегрирующего множителя
Показано как распознать дифференциальное уравнение в полных дифференциалах. Даны методы его решения. Приводится пример решения уравнения в полных дифференциалах двумя способами. Решение дифференциальных уравнений с помощью интегрирующего множителя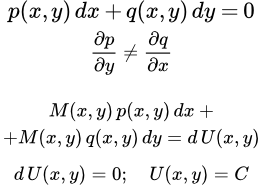 Рассмотрен метод решения дифференциальных уравнений первого порядка с помощью интегрирующего множителя. Приведены свойства интегрирующих множителей и указаны методы их нахождения. Разобраны примеры решений уравнений с помощью интегрирующего множителя. Теорема Коши существования и единственности решения дифференциального уравнения первого порядка
Рассмотрен метод решения дифференциальных уравнений первого порядка с помощью интегрирующего множителя. Приведены свойства интегрирующих множителей и указаны методы их нахождения. Разобраны примеры решений уравнений с помощью интегрирующего множителя. Теорема Коши существования и единственности решения дифференциального уравнения первого порядка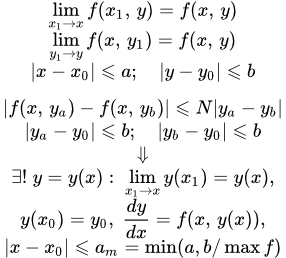 Формулировка теоремы Коши существования и единственности решения дифференциального уравнения первого порядка. Доказательство теоремы методом последовательных приближений Пикара.
Формулировка теоремы Коши существования и единственности решения дифференциального уравнения первого порядка. Доказательство теоремы методом последовательных приближений Пикара. Не разрешенные относительно производной
Дифференциальные уравнения первого порядка, не разрешенные относительно производной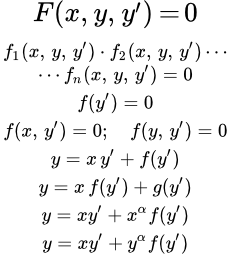 Приводятся основные виды обыкновенных дифференциальных уравнений первого порядка, не разрешенные относительно производной. Разобраны самые простые из них и даны ссылки на страницы, содержащие методы их решения с примерами. Дифференциальные уравнения первого порядка, содержащие только производную
Приводятся основные виды обыкновенных дифференциальных уравнений первого порядка, не разрешенные относительно производной. Разобраны самые простые из них и даны ссылки на страницы, содержащие методы их решения с примерами. Дифференциальные уравнения первого порядка, содержащие только производную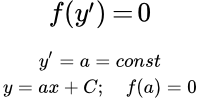 Рассмотрено решение дифференциальных уравнений первого порядка, содержащих только производную. Приводится пример решения такого уравнения. Дифференциальные уравнения, не содержащие одну из переменных
Рассмотрено решение дифференциальных уравнений первого порядка, содержащих только производную. Приводится пример решения такого уравнения. Дифференциальные уравнения, не содержащие одну из переменных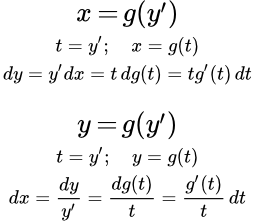 Дан метод решения дифференциальных уравнений, не разрешенных относительно производной, не содержащих в явном виде одну из переменных. Рассмотрен частный случай, когда уравнение может быть разрешено относительно переменной. Приводятся примеры решений таких уравнений. Дифференциальное уравнение Клеро
Дан метод решения дифференциальных уравнений, не разрешенных относительно производной, не содержащих в явном виде одну из переменных. Рассмотрен частный случай, когда уравнение может быть разрешено относительно переменной. Приводятся примеры решений таких уравнений. Дифференциальное уравнение Клеро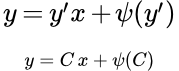 Рассмотрен метод решения дифференциального уравнения Клеро и нахождение его особого решения. Дан пример решения дифференциального уравнения Клеро. Дифференциальное уравнение Лагранжа
Рассмотрен метод решения дифференциального уравнения Клеро и нахождение его особого решения. Дан пример решения дифференциального уравнения Клеро. Дифференциальное уравнение Лагранжа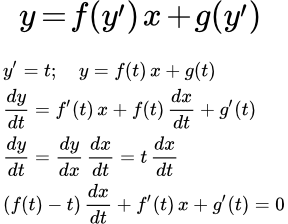 Рассмотрен метод решения дифференциального уравнения Лагранжа. Дан пример подробного решения дифференциального уравнения Лагранжа. Дифференциальные уравнения, не разрешенные относительно производной, приводящиеся к уравнению Бернулли
Рассмотрен метод решения дифференциального уравнения Лагранжа. Дан пример подробного решения дифференциального уравнения Лагранжа. Дифференциальные уравнения, не разрешенные относительно производной, приводящиеся к уравнению Бернулли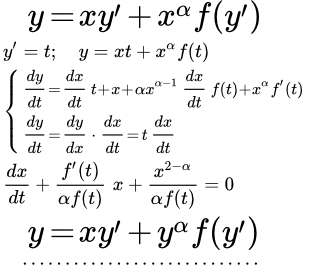 Рассмотрен метод решения дифференциальных уравнений, не разрешенных относительно производной, приводящихся к уравнению Бернулли.
Рассмотрен метод решения дифференциальных уравнений, не разрешенных относительно производной, приводящихся к уравнению Бернулли.
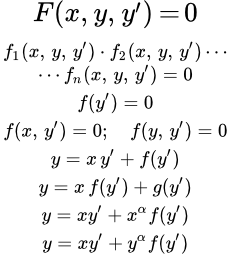 Приводятся основные виды обыкновенных дифференциальных уравнений первого порядка, не разрешенные относительно производной. Разобраны самые простые из них и даны ссылки на страницы, содержащие методы их решения с примерами. Дифференциальные уравнения первого порядка, содержащие только производную
Приводятся основные виды обыкновенных дифференциальных уравнений первого порядка, не разрешенные относительно производной. Разобраны самые простые из них и даны ссылки на страницы, содержащие методы их решения с примерами. Дифференциальные уравнения первого порядка, содержащие только производную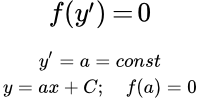 Рассмотрено решение дифференциальных уравнений первого порядка, содержащих только производную. Приводится пример решения такого уравнения. Дифференциальные уравнения, не содержащие одну из переменных
Рассмотрено решение дифференциальных уравнений первого порядка, содержащих только производную. Приводится пример решения такого уравнения. Дифференциальные уравнения, не содержащие одну из переменных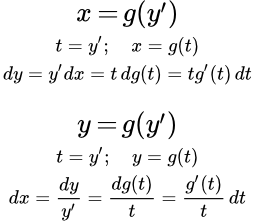 Дан метод решения дифференциальных уравнений, не разрешенных относительно производной, не содержащих в явном виде одну из переменных. Рассмотрен частный случай, когда уравнение может быть разрешено относительно переменной. Приводятся примеры решений таких уравнений. Дифференциальное уравнение Клеро
Дан метод решения дифференциальных уравнений, не разрешенных относительно производной, не содержащих в явном виде одну из переменных. Рассмотрен частный случай, когда уравнение может быть разрешено относительно переменной. Приводятся примеры решений таких уравнений. Дифференциальное уравнение Клеро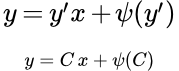 Рассмотрен метод решения дифференциального уравнения Клеро и нахождение его особого решения. Дан пример решения дифференциального уравнения Клеро. Дифференциальное уравнение Лагранжа
Рассмотрен метод решения дифференциального уравнения Клеро и нахождение его особого решения. Дан пример решения дифференциального уравнения Клеро. Дифференциальное уравнение Лагранжа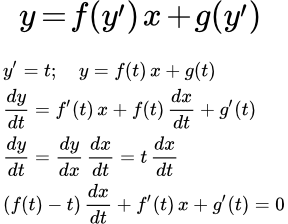 Рассмотрен метод решения дифференциального уравнения Лагранжа. Дан пример подробного решения дифференциального уравнения Лагранжа. Дифференциальные уравнения, не разрешенные относительно производной, приводящиеся к уравнению Бернулли
Рассмотрен метод решения дифференциального уравнения Лагранжа. Дан пример подробного решения дифференциального уравнения Лагранжа. Дифференциальные уравнения, не разрешенные относительно производной, приводящиеся к уравнению Бернулли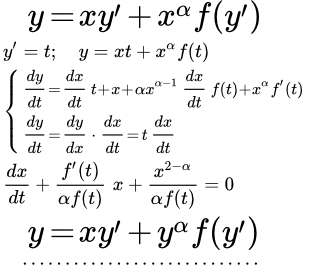 Рассмотрен метод решения дифференциальных уравнений, не разрешенных относительно производной, приводящихся к уравнению Бернулли.
Рассмотрен метод решения дифференциальных уравнений, не разрешенных относительно производной, приводящихся к уравнению Бернулли. Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков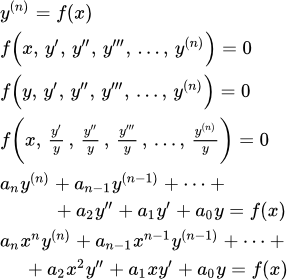 Перечислены основные типы обыкновенных дифференциальных уравнений (ДУ) высших порядков, допускающие решение. Кратко изложены методы их решения. Указаны ссылки на страницы, с подробным описанием методов решения и примерами. Дифференциальное уравнение y(n) = f(x)
Перечислены основные типы обыкновенных дифференциальных уравнений (ДУ) высших порядков, допускающие решение. Кратко изложены методы их решения. Указаны ссылки на страницы, с подробным описанием методов решения и примерами. Дифференциальное уравнение y(n) = f(x)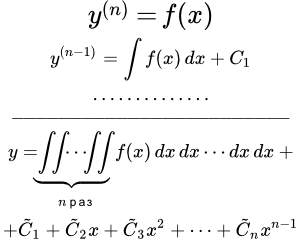 Рассмотрено дифференциальное уравнение, в котором n-я производная равна функции от независимой переменной x. Такое уравнение решается непосредственным интегрированием n раз. Также его можно решить, выполняя однократное интегрирование с помощью формулы Коши для повторных интегралов. Дан подробный пример решения такого уравнения. Формула Коши для повторных интегралов
Рассмотрено дифференциальное уравнение, в котором n-я производная равна функции от независимой переменной x. Такое уравнение решается непосредственным интегрированием n раз. Также его можно решить, выполняя однократное интегрирование с помощью формулы Коши для повторных интегралов. Дан подробный пример решения такого уравнения. Формула Коши для повторных интегралов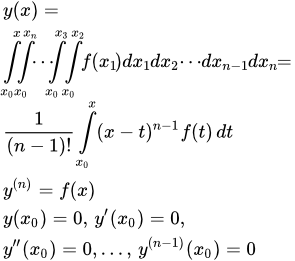 Доказана формула Коши, которая сводит повторные интегралы от некоторой функции f к однократному. Показано, что эти интегралы являются частным решением дифференциального уравнения, в котором производная n-ой степени от y равна f(x), с нулевыми начальными условиями. Дано общее решение такого уравнения.
Доказана формула Коши, которая сводит повторные интегралы от некоторой функции f к однократному. Показано, что эти интегралы являются частным решением дифференциального уравнения, в котором производная n-ой степени от y равна f(x), с нулевыми начальными условиями. Дано общее решение такого уравнения. 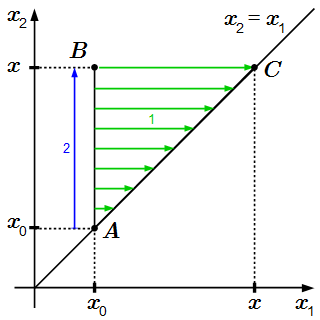 Интегрируем по x1, а затем по x2.
Интегрируем по x1, а затем по x2. 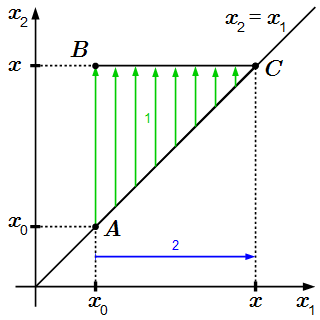 Интегрируем по x2, а затем по x1. Дифференциальные уравнения высших порядков, решаемые в квадратурах
Интегрируем по x2, а затем по x1. Дифференциальные уравнения высших порядков, решаемые в квадратурах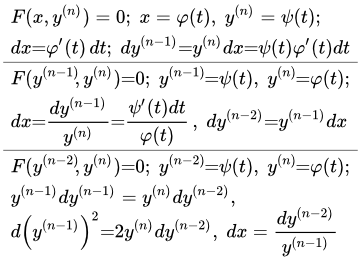 Приводятся типы обыкновенных дифференциальных уравнений (ДУ) высших порядков, решаемых в квадратурах. Подробно изложены методы их решения. Разобраны пять примеров решений подобных задач. Дифференциальные уравнения высших порядков, не содержащие функцию в явном виде
Приводятся типы обыкновенных дифференциальных уравнений (ДУ) высших порядков, решаемых в квадратурах. Подробно изложены методы их решения. Разобраны пять примеров решений подобных задач. Дифференциальные уравнения высших порядков, не содержащие функцию в явном виде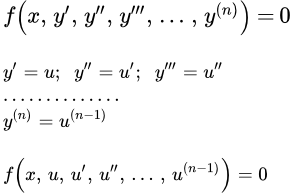 Рассмотрен метод решения дифференциального уравнения высшего порядка, не содержащего функцию y в явном виде. В таком уравнении порядок понижается с помощью подстановки. Дан подробный пример решения такого уравнения. Дифференциальные уравнения высших порядков, не содержащие переменную в явном виде
Рассмотрен метод решения дифференциального уравнения высшего порядка, не содержащего функцию y в явном виде. В таком уравнении порядок понижается с помощью подстановки. Дан подробный пример решения такого уравнения. Дифференциальные уравнения высших порядков, не содержащие переменную в явном виде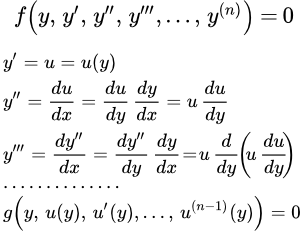 Рассмотрен метод решения дифференциального уравнения высшего порядка, не содержащего переменную x в явном виде. Такое уравнение сводится к уравнению более низкого порядка с помощью подстановки. Дан подробный пример решения такого уравнения. Однородные относительно функции и ее производных дифференциальные уравнения высших порядков
Рассмотрен метод решения дифференциального уравнения высшего порядка, не содержащего переменную x в явном виде. Такое уравнение сводится к уравнению более низкого порядка с помощью подстановки. Дан подробный пример решения такого уравнения. Однородные относительно функции и ее производных дифференциальные уравнения высших порядков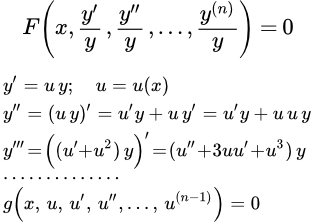 Показано как распознать дифференциальное уравнение, однородное относительно функции и ее производных. Рассмотрен способ решения таких уравнений. Дан пример подробного решения однородного дифференциального уравнения второго порядка. Обобщенно однородные дифференциальные уравнения относительно переменных высших порядков
Показано как распознать дифференциальное уравнение, однородное относительно функции и ее производных. Рассмотрен способ решения таких уравнений. Дан пример подробного решения однородного дифференциального уравнения второго порядка. Обобщенно однородные дифференциальные уравнения относительно переменных высших порядков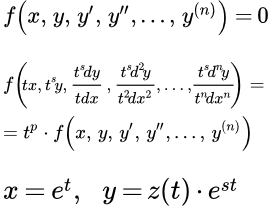 Дано определение и указано как распознать обобщенно однородное относительно переменных дифференциальное уравнение высшего порядка. Приводится подстановка, с помощью которой в этом уравнении можно понизить порядок. Подробно рассмотрен пример решения обобщенно однородного ДУ второго порядка. Дифференциальные уравнения высших порядков с полной производной
Дано определение и указано как распознать обобщенно однородное относительно переменных дифференциальное уравнение высшего порядка. Приводится подстановка, с помощью которой в этом уравнении можно понизить порядок. Подробно рассмотрен пример решения обобщенно однородного ДУ второго порядка. Дифференциальные уравнения высших порядков с полной производной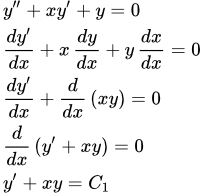 Показано как понизить порядок дифференциального уравнения с полной (точной) производной. Рассмотрены методы выделения полной производной, и примеры применения этих методов для решения дифференциальных уравнений высших порядков. Теорема существования и единственности решения дифференциального уравнения произвольного порядка
Показано как понизить порядок дифференциального уравнения с полной (точной) производной. Рассмотрены методы выделения полной производной, и примеры применения этих методов для решения дифференциальных уравнений высших порядков. Теорема существования и единственности решения дифференциального уравнения произвольного порядка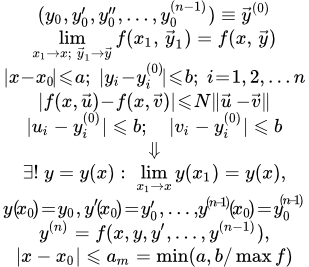 Формулировка и доказательство теоремы существования и единственности решения дифференциального уравнения произвольного порядка. Доказательство производится путем сведения уравнения к системе уравнений первого порядка. Теорема существования и единственности решения системы дифференциальных уравнений
Формулировка и доказательство теоремы существования и единственности решения дифференциального уравнения произвольного порядка. Доказательство производится путем сведения уравнения к системе уравнений первого порядка. Теорема существования и единственности решения системы дифференциальных уравнений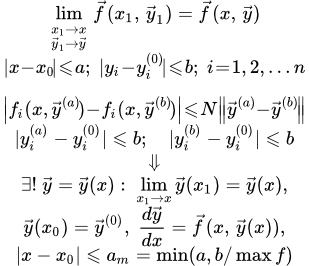 Формулировка и доказательство теоремы существования и единственности решения системы дифференциальных уравнений методом последовательных приближений Пикара.
Формулировка и доказательство теоремы существования и единственности решения системы дифференциальных уравнений методом последовательных приближений Пикара.
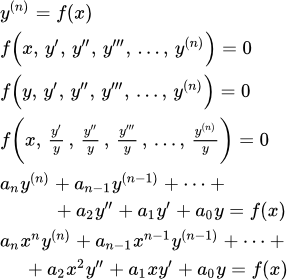 Перечислены основные типы обыкновенных дифференциальных уравнений (ДУ) высших порядков, допускающие решение. Кратко изложены методы их решения. Указаны ссылки на страницы, с подробным описанием методов решения и примерами. Дифференциальное уравнение y(n) = f(x)
Перечислены основные типы обыкновенных дифференциальных уравнений (ДУ) высших порядков, допускающие решение. Кратко изложены методы их решения. Указаны ссылки на страницы, с подробным описанием методов решения и примерами. Дифференциальное уравнение y(n) = f(x)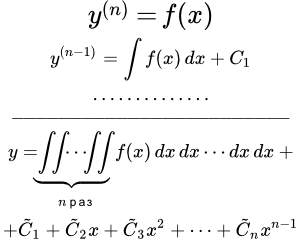 Рассмотрено дифференциальное уравнение, в котором n-я производная равна функции от независимой переменной x. Такое уравнение решается непосредственным интегрированием n раз. Также его можно решить, выполняя однократное интегрирование с помощью формулы Коши для повторных интегралов. Дан подробный пример решения такого уравнения. Формула Коши для повторных интегралов
Рассмотрено дифференциальное уравнение, в котором n-я производная равна функции от независимой переменной x. Такое уравнение решается непосредственным интегрированием n раз. Также его можно решить, выполняя однократное интегрирование с помощью формулы Коши для повторных интегралов. Дан подробный пример решения такого уравнения. Формула Коши для повторных интегралов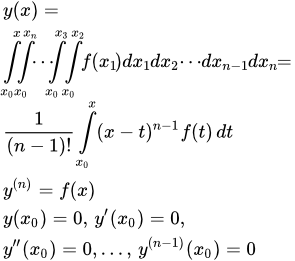 Доказана формула Коши, которая сводит повторные интегралы от некоторой функции f к однократному. Показано, что эти интегралы являются частным решением дифференциального уравнения, в котором производная n-ой степени от y равна f(x), с нулевыми начальными условиями. Дано общее решение такого уравнения.
Доказана формула Коши, которая сводит повторные интегралы от некоторой функции f к однократному. Показано, что эти интегралы являются частным решением дифференциального уравнения, в котором производная n-ой степени от y равна f(x), с нулевыми начальными условиями. Дано общее решение такого уравнения.  Интегрируем по x1, а затем по x2.
Интегрируем по x1, а затем по x2.  Интегрируем по x2, а затем по x1. Дифференциальные уравнения высших порядков, решаемые в квадратурах
Интегрируем по x2, а затем по x1. Дифференциальные уравнения высших порядков, решаемые в квадратурах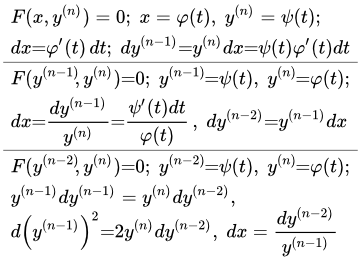 Приводятся типы обыкновенных дифференциальных уравнений (ДУ) высших порядков, решаемых в квадратурах. Подробно изложены методы их решения. Разобраны пять примеров решений подобных задач. Дифференциальные уравнения высших порядков, не содержащие функцию в явном виде
Приводятся типы обыкновенных дифференциальных уравнений (ДУ) высших порядков, решаемых в квадратурах. Подробно изложены методы их решения. Разобраны пять примеров решений подобных задач. Дифференциальные уравнения высших порядков, не содержащие функцию в явном виде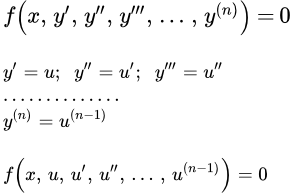 Рассмотрен метод решения дифференциального уравнения высшего порядка, не содержащего функцию y в явном виде. В таком уравнении порядок понижается с помощью подстановки. Дан подробный пример решения такого уравнения. Дифференциальные уравнения высших порядков, не содержащие переменную в явном виде
Рассмотрен метод решения дифференциального уравнения высшего порядка, не содержащего функцию y в явном виде. В таком уравнении порядок понижается с помощью подстановки. Дан подробный пример решения такого уравнения. Дифференциальные уравнения высших порядков, не содержащие переменную в явном виде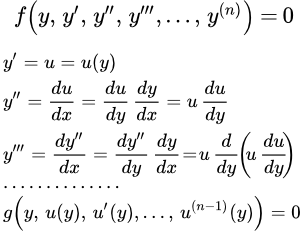 Рассмотрен метод решения дифференциального уравнения высшего порядка, не содержащего переменную x в явном виде. Такое уравнение сводится к уравнению более низкого порядка с помощью подстановки. Дан подробный пример решения такого уравнения. Однородные относительно функции и ее производных дифференциальные уравнения высших порядков
Рассмотрен метод решения дифференциального уравнения высшего порядка, не содержащего переменную x в явном виде. Такое уравнение сводится к уравнению более низкого порядка с помощью подстановки. Дан подробный пример решения такого уравнения. Однородные относительно функции и ее производных дифференциальные уравнения высших порядков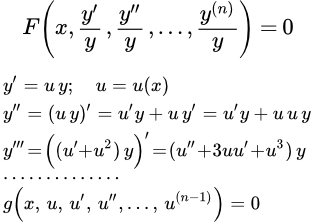 Показано как распознать дифференциальное уравнение, однородное относительно функции и ее производных. Рассмотрен способ решения таких уравнений. Дан пример подробного решения однородного дифференциального уравнения второго порядка. Обобщенно однородные дифференциальные уравнения относительно переменных высших порядков
Показано как распознать дифференциальное уравнение, однородное относительно функции и ее производных. Рассмотрен способ решения таких уравнений. Дан пример подробного решения однородного дифференциального уравнения второго порядка. Обобщенно однородные дифференциальные уравнения относительно переменных высших порядков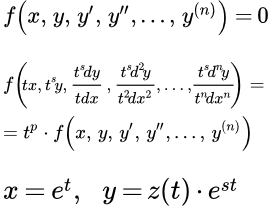 Дано определение и указано как распознать обобщенно однородное относительно переменных дифференциальное уравнение высшего порядка. Приводится подстановка, с помощью которой в этом уравнении можно понизить порядок. Подробно рассмотрен пример решения обобщенно однородного ДУ второго порядка. Дифференциальные уравнения высших порядков с полной производной
Дано определение и указано как распознать обобщенно однородное относительно переменных дифференциальное уравнение высшего порядка. Приводится подстановка, с помощью которой в этом уравнении можно понизить порядок. Подробно рассмотрен пример решения обобщенно однородного ДУ второго порядка. Дифференциальные уравнения высших порядков с полной производной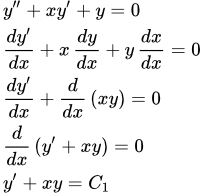 Показано как понизить порядок дифференциального уравнения с полной (точной) производной. Рассмотрены методы выделения полной производной, и примеры применения этих методов для решения дифференциальных уравнений высших порядков. Теорема существования и единственности решения дифференциального уравнения произвольного порядка
Показано как понизить порядок дифференциального уравнения с полной (точной) производной. Рассмотрены методы выделения полной производной, и примеры применения этих методов для решения дифференциальных уравнений высших порядков. Теорема существования и единственности решения дифференциального уравнения произвольного порядка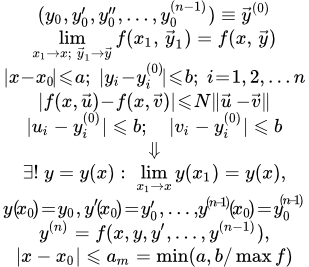 Формулировка и доказательство теоремы существования и единственности решения дифференциального уравнения произвольного порядка. Доказательство производится путем сведения уравнения к системе уравнений первого порядка. Теорема существования и единственности решения системы дифференциальных уравнений
Формулировка и доказательство теоремы существования и единственности решения дифференциального уравнения произвольного порядка. Доказательство производится путем сведения уравнения к системе уравнений первого порядка. Теорема существования и единственности решения системы дифференциальных уравнений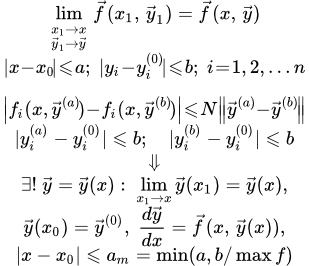 Формулировка и доказательство теоремы существования и единственности решения системы дифференциальных уравнений методом последовательных приближений Пикара.
Формулировка и доказательство теоремы существования и единственности решения системы дифференциальных уравнений методом последовательных приближений Пикара. Линейные с постоянными коэффициентами
Линейные дифференциальные уравнения с постоянными коэффициентами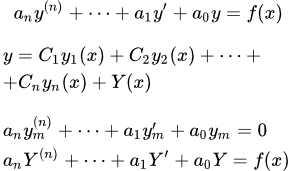 Даны определения линейных дифференциальных уравнений с постоянными коэффициентами (однородных, неоднородных и общее определение). Рассмотрены свойства их решений. Решение дифференциальных уравнений высших порядков методом Бернулли
Даны определения линейных дифференциальных уравнений с постоянными коэффициентами (однородных, неоднородных и общее определение). Рассмотрены свойства их решений. Решение дифференциальных уравнений высших порядков методом Бернулли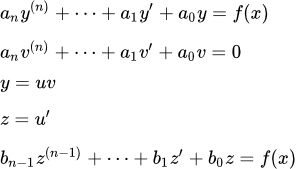 Рассмотрен метод Бернулли (двух функций) для решения линейных неоднородных дифференциальных уравнений высших порядков. Этот метод применим, если известно частное решение однородного уравнения. Приведены примеры решений линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами методом Бернулли. Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа
Рассмотрен метод Бернулли (двух функций) для решения линейных неоднородных дифференциальных уравнений высших порядков. Этот метод применим, если известно частное решение однородного уравнения. Приведены примеры решений линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами методом Бернулли. Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа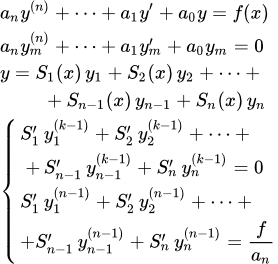 Рассмотрен метод решения линейных неоднородных дифференциальных уравнений высших порядков с постоянными коэффициентами методом вариации постоянных Лагранжа. Метод Лагранжа также применим для решения любых линейных неоднородных уравнений, если известна фундаментальная система решений однородного уравнения. Примеры решений дифференциальных уравнений второго порядка методом Лагранжа
Рассмотрен метод решения линейных неоднородных дифференциальных уравнений высших порядков с постоянными коэффициентами методом вариации постоянных Лагранжа. Метод Лагранжа также применим для решения любых линейных неоднородных уравнений, если известна фундаментальная система решений однородного уравнения. Примеры решений дифференциальных уравнений второго порядка методом Лагранжа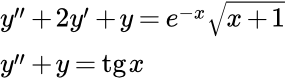 Рассмотрены примеры решений линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами методом Лагранжа (вариации постоянных). Понижение порядка в линейных неоднородных ДУ с постоянными коэффициентами
Рассмотрены примеры решений линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами методом Лагранжа (вариации постоянных). Понижение порядка в линейных неоднородных ДУ с постоянными коэффициентами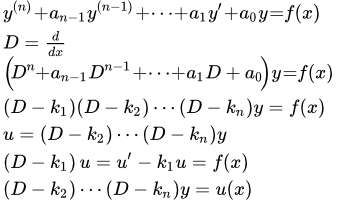 Рассмотрен способ решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами методом понижения порядка. Пример решения линейного неоднородного дифференциального уравнения методом понижения порядка
Рассмотрен способ решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами методом понижения порядка. Пример решения линейного неоднородного дифференциального уравнения методом понижения порядка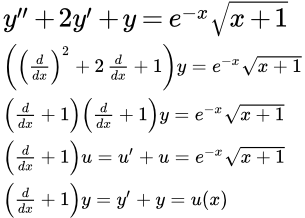 Рассмотрен пример решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами, характеристическое уравнение которого имеет действительные корни, методом понижения порядка. Пример комплексной подстановки при решении линейного неоднородного дифференциального уравнения
Рассмотрен пример решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами, характеристическое уравнение которого имеет действительные корни, методом понижения порядка. Пример комплексной подстановки при решении линейного неоднородного дифференциального уравнения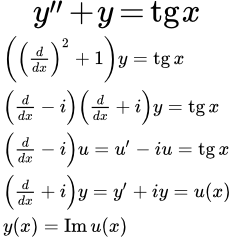 Рассмотрен пример применения комплексной подстановки при решении линейного неоднородного дифференциального уравнения с постоянными коэффициентами. Если характеристическое уравнение имеет комплексные корни, то подстановка позволяет понизить порядок уравнения на две единицы. Решение линейных однородных дифференциальных уравнений с постоянными коэффициентами
Рассмотрен пример применения комплексной подстановки при решении линейного неоднородного дифференциального уравнения с постоянными коэффициентами. Если характеристическое уравнение имеет комплексные корни, то подстановка позволяет понизить порядок уравнения на две единицы. Решение линейных однородных дифференциальных уравнений с постоянными коэффициентами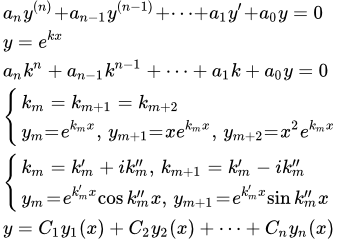 Рассмотрен способ решения линейных однородных дифференциальных уравнений высших порядков с постоянными коэффициентами. Дан вид общего решения. Примеры решений. Решение линейных дифференциальных уравнений с постоянными коэффициентами со специальной неоднородной частью
Рассмотрен способ решения линейных однородных дифференциальных уравнений высших порядков с постоянными коэффициентами. Дан вид общего решения. Примеры решений. Решение линейных дифференциальных уравнений с постоянными коэффициентами со специальной неоднородной частью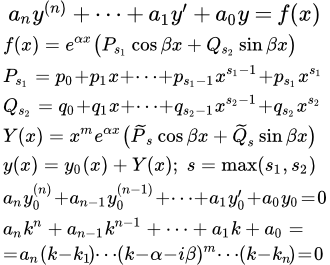 Рассмотрен метод решения линейных дифференциальных уравнений высших порядков с постоянными коэффициентами со специальной неоднородной частью, содержащей комбинации из многочленов, экспонент, синусов и косинусов. Установлен вид частного решения. Пример решения линейного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью
Рассмотрен метод решения линейных дифференциальных уравнений высших порядков с постоянными коэффициентами со специальной неоднородной частью, содержащей комбинации из многочленов, экспонент, синусов и косинусов. Установлен вид частного решения. Пример решения линейного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью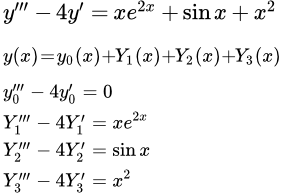 Рассмотрен пример решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью в виде суммы экспоненты, умноженной на x, синуса и многочлена второй степени. y′′+y=x2cos x. Пример решения линейного дифференциального уравнения со специальной неоднородной частью
Рассмотрен пример решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью в виде суммы экспоненты, умноженной на x, синуса и многочлена второй степени. y′′+y=x2cos x. Пример решения линейного дифференциального уравнения со специальной неоднородной частью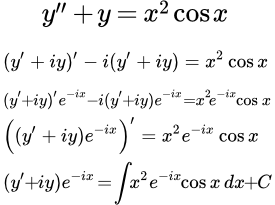 Пример решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью y′′+y=x∧2cos x. Приводится подробное решение тремя способами: понижением порядка линейной подстановкой; стандартным способом; стандартным способом, используя комплексные функции. Дифференциальное уравнение Эйлера и методы его решения
Пример решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью y′′+y=x∧2cos x. Приводится подробное решение тремя способами: понижением порядка линейной подстановкой; стандартным способом; стандартным способом, используя комплексные функции. Дифференциальное уравнение Эйлера и методы его решения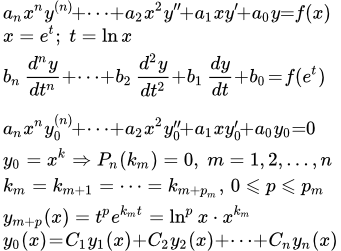 Определение дифференциального уравнения Эйлера. Рассмотрены методы его решения. Примеры решений однородных дифференциальных уравнений Эйлера
Определение дифференциального уравнения Эйлера. Рассмотрены методы его решения. Примеры решений однородных дифференциальных уравнений Эйлера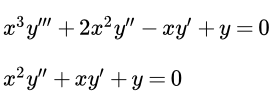 Рассмотрены примеры решений однородных дифференциальных уравнений Эйлера. Пример решения неоднородного дифференциального уравнения Эйлера второго порядка
Рассмотрены примеры решений однородных дифференциальных уравнений Эйлера. Пример решения неоднородного дифференциального уравнения Эйлера второго порядка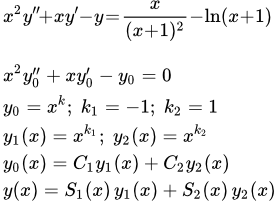 Рассмотрен пример решения неоднородного дифференциального уравнения Эйлера второго порядка методом вариации постоянных Лагранжа.
Рассмотрен пример решения неоднородного дифференциального уравнения Эйлера второго порядка методом вариации постоянных Лагранжа.
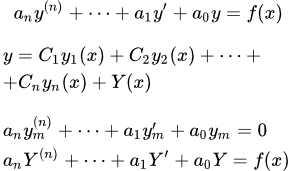 Даны определения линейных дифференциальных уравнений с постоянными коэффициентами (однородных, неоднородных и общее определение). Рассмотрены свойства их решений. Решение дифференциальных уравнений высших порядков методом Бернулли
Даны определения линейных дифференциальных уравнений с постоянными коэффициентами (однородных, неоднородных и общее определение). Рассмотрены свойства их решений. Решение дифференциальных уравнений высших порядков методом Бернулли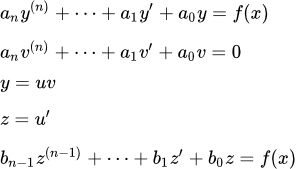 Рассмотрен метод Бернулли (двух функций) для решения линейных неоднородных дифференциальных уравнений высших порядков. Этот метод применим, если известно частное решение однородного уравнения. Приведены примеры решений линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами методом Бернулли. Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа
Рассмотрен метод Бернулли (двух функций) для решения линейных неоднородных дифференциальных уравнений высших порядков. Этот метод применим, если известно частное решение однородного уравнения. Приведены примеры решений линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами методом Бернулли. Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа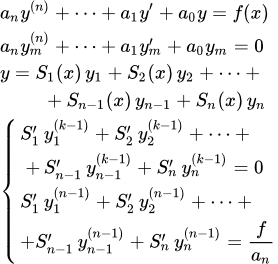 Рассмотрен метод решения линейных неоднородных дифференциальных уравнений высших порядков с постоянными коэффициентами методом вариации постоянных Лагранжа. Метод Лагранжа также применим для решения любых линейных неоднородных уравнений, если известна фундаментальная система решений однородного уравнения. Примеры решений дифференциальных уравнений второго порядка методом Лагранжа
Рассмотрен метод решения линейных неоднородных дифференциальных уравнений высших порядков с постоянными коэффициентами методом вариации постоянных Лагранжа. Метод Лагранжа также применим для решения любых линейных неоднородных уравнений, если известна фундаментальная система решений однородного уравнения. Примеры решений дифференциальных уравнений второго порядка методом Лагранжа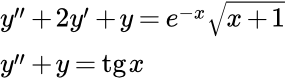 Рассмотрены примеры решений линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами методом Лагранжа (вариации постоянных). Понижение порядка в линейных неоднородных ДУ с постоянными коэффициентами
Рассмотрены примеры решений линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами методом Лагранжа (вариации постоянных). Понижение порядка в линейных неоднородных ДУ с постоянными коэффициентами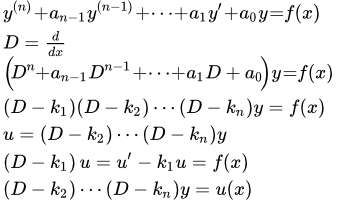 Рассмотрен способ решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами методом понижения порядка. Пример решения линейного неоднородного дифференциального уравнения методом понижения порядка
Рассмотрен способ решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами методом понижения порядка. Пример решения линейного неоднородного дифференциального уравнения методом понижения порядка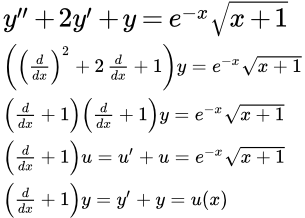 Рассмотрен пример решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами, характеристическое уравнение которого имеет действительные корни, методом понижения порядка. Пример комплексной подстановки при решении линейного неоднородного дифференциального уравнения
Рассмотрен пример решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами, характеристическое уравнение которого имеет действительные корни, методом понижения порядка. Пример комплексной подстановки при решении линейного неоднородного дифференциального уравнения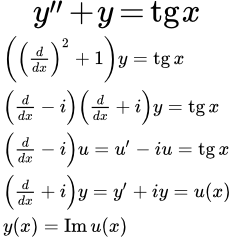 Рассмотрен пример применения комплексной подстановки при решении линейного неоднородного дифференциального уравнения с постоянными коэффициентами. Если характеристическое уравнение имеет комплексные корни, то подстановка позволяет понизить порядок уравнения на две единицы. Решение линейных однородных дифференциальных уравнений с постоянными коэффициентами
Рассмотрен пример применения комплексной подстановки при решении линейного неоднородного дифференциального уравнения с постоянными коэффициентами. Если характеристическое уравнение имеет комплексные корни, то подстановка позволяет понизить порядок уравнения на две единицы. Решение линейных однородных дифференциальных уравнений с постоянными коэффициентами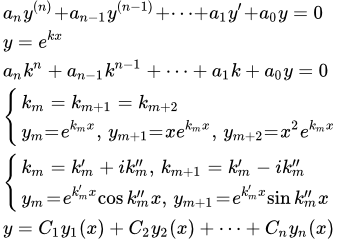 Рассмотрен способ решения линейных однородных дифференциальных уравнений высших порядков с постоянными коэффициентами. Дан вид общего решения. Примеры решений. Решение линейных дифференциальных уравнений с постоянными коэффициентами со специальной неоднородной частью
Рассмотрен способ решения линейных однородных дифференциальных уравнений высших порядков с постоянными коэффициентами. Дан вид общего решения. Примеры решений. Решение линейных дифференциальных уравнений с постоянными коэффициентами со специальной неоднородной частью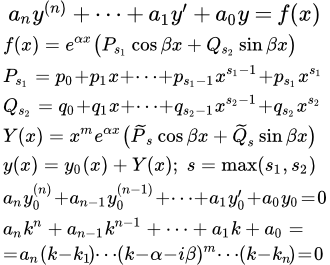 Рассмотрен метод решения линейных дифференциальных уравнений высших порядков с постоянными коэффициентами со специальной неоднородной частью, содержащей комбинации из многочленов, экспонент, синусов и косинусов. Установлен вид частного решения. Пример решения линейного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью
Рассмотрен метод решения линейных дифференциальных уравнений высших порядков с постоянными коэффициентами со специальной неоднородной частью, содержащей комбинации из многочленов, экспонент, синусов и косинусов. Установлен вид частного решения. Пример решения линейного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью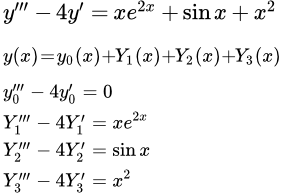 Рассмотрен пример решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью в виде суммы экспоненты, умноженной на x, синуса и многочлена второй степени. y′′+y=x2cos x. Пример решения линейного дифференциального уравнения со специальной неоднородной частью
Рассмотрен пример решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью в виде суммы экспоненты, умноженной на x, синуса и многочлена второй степени. y′′+y=x2cos x. Пример решения линейного дифференциального уравнения со специальной неоднородной частью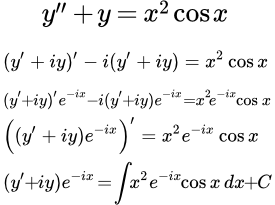 Пример решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью y′′+y=x∧2cos x. Приводится подробное решение тремя способами: понижением порядка линейной подстановкой; стандартным способом; стандартным способом, используя комплексные функции. Дифференциальное уравнение Эйлера и методы его решения
Пример решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами со специальной неоднородной частью y′′+y=x∧2cos x. Приводится подробное решение тремя способами: понижением порядка линейной подстановкой; стандартным способом; стандартным способом, используя комплексные функции. Дифференциальное уравнение Эйлера и методы его решения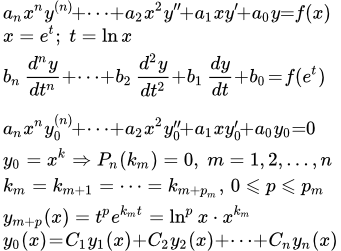 Определение дифференциального уравнения Эйлера. Рассмотрены методы его решения. Примеры решений однородных дифференциальных уравнений Эйлера
Определение дифференциального уравнения Эйлера. Рассмотрены методы его решения. Примеры решений однородных дифференциальных уравнений Эйлера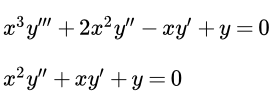 Рассмотрены примеры решений однородных дифференциальных уравнений Эйлера. Пример решения неоднородного дифференциального уравнения Эйлера второго порядка
Рассмотрены примеры решений однородных дифференциальных уравнений Эйлера. Пример решения неоднородного дифференциального уравнения Эйлера второго порядка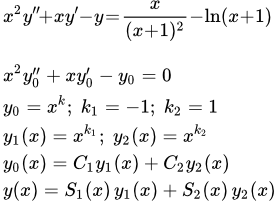 Рассмотрен пример решения неоднородного дифференциального уравнения Эйлера второго порядка методом вариации постоянных Лагранжа.
Рассмотрен пример решения неоднородного дифференциального уравнения Эйлера второго порядка методом вариации постоянных Лагранжа. Линейные уравнения в частных производных первого порядка
См. также: