Линейное программирование в картинках
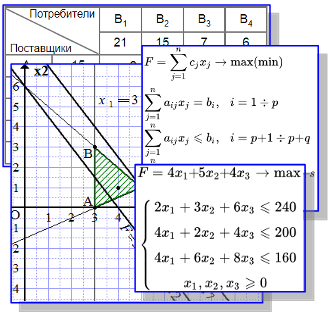
Описания и картинки страниц раздела «Линейное программирование». Приводятся основные результаты раздела в сжатом виде – в виде изображений. Картинки сопровождаются заголовками, описаниями страниц и ссылками на них.
Содержание
Основы линейного программирования
Основы линейного программирования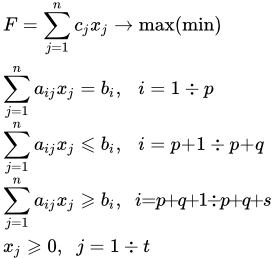
Основные понятия, определения и теоремы линейного программирования. Свойства решений задач ЛП и их графическая интерпретация. Пример решения задачи линейного программирования тремя способами: графическим, методом перебора вершин и симплексным методом. Пример решения транспортной задачи методом потенциалов. 
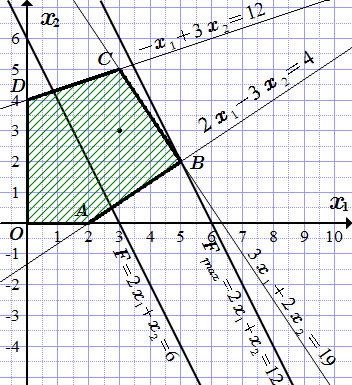Решение задачи линейного программирования графическим методом. 
Заполняем верхнюю левую ячейку, и вычеркиваем первую строку. 
Заполняем верхнюю левую ячейку предыдущей таблицы, и вычеркиваем первый столбец.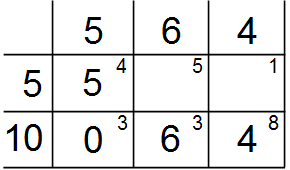 
Первый опорный план. 
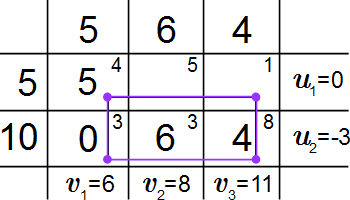Потенциалы и контур клетки (1,3). 
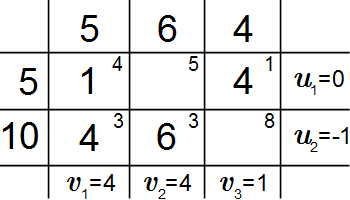Второй опорный план. Решение задач линейного программирования графическим методом
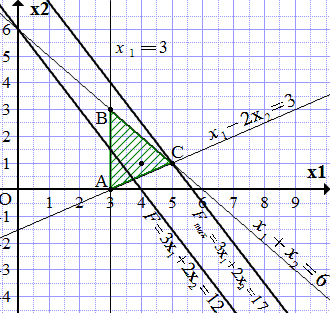Рассмотрено решение задач линейного программирования графическим методом. Описание метода. Примеры решения задач. 
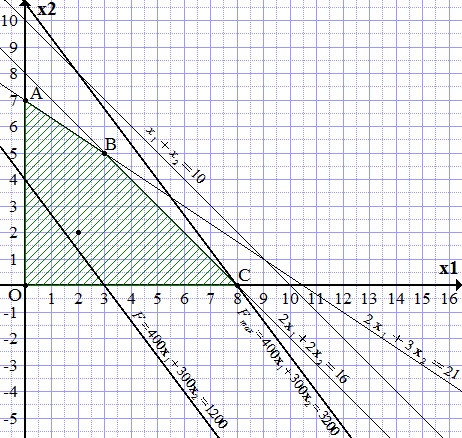Построение области допустимых решений 
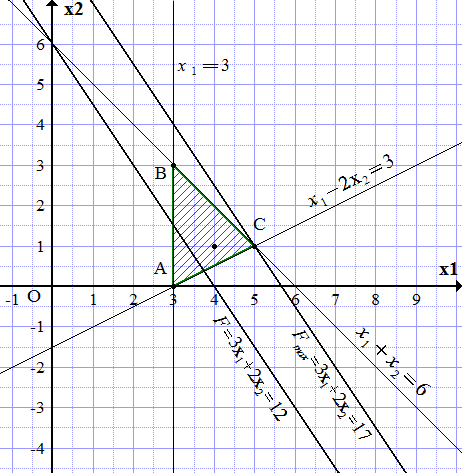Область допустимых решений 
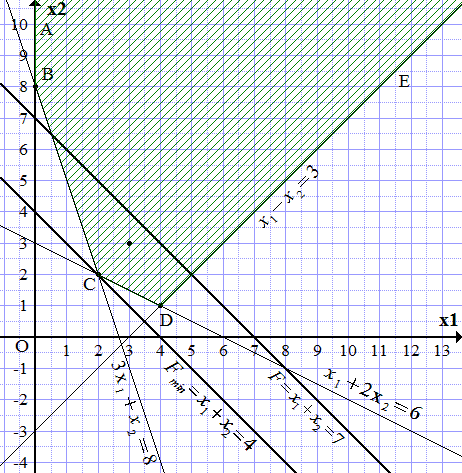Неограниченная область допустимых решений Правила составления двойственных задач линейного программирования
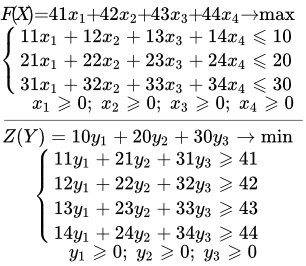Представлены правила составления двойственных задач. Рассмотрены симметричные, несимметричные и смешанные пары. Разобраны примеры составления двойственных задач. Решение двойственной задачи
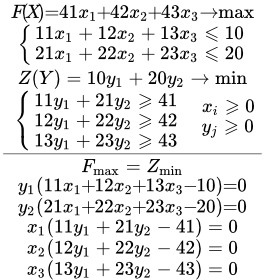Приводятся формулировки первой и второй теорем двойственности. Показано, как получить решение двойственной задачи из решения прямой, применяя эти теоремы. Подробно разобраны примеры решений задач. Онлайн калькулятор для составления и решения двойственной задачи
Онлайн калькулятор позволяет к исходной задаче линейного программирования составить двойственную задачу, и решить обе задачи.
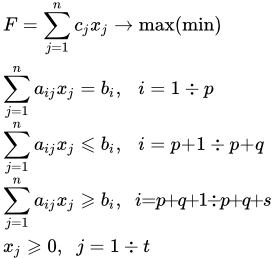Основные понятия, определения и теоремы линейного программирования. Свойства решений задач ЛП и их графическая интерпретация. Пример решения задачи линейного программирования тремя способами: графическим, методом перебора вершин и симплексным методом. Пример решения транспортной задачи методом потенциалов. Решение задачи линейного программирования графическим методом. Заполняем верхнюю левую ячейку, и вычеркиваем первую строку. Заполняем верхнюю левую ячейку предыдущей таблицы, и вычеркиваем первый столбец. Первый опорный план. Потенциалы и контур клетки (1,3). 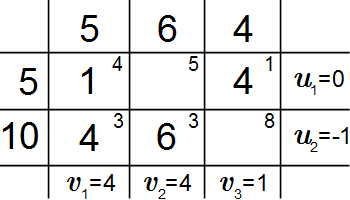Второй опорный план. Решение задач линейного программирования графическим методомРассмотрено решение задач линейного программирования графическим методом. Описание метода. Примеры решения задач. Построение области допустимых решений Область допустимых решений Неограниченная область допустимых решений Правила составления двойственных задач линейного программирования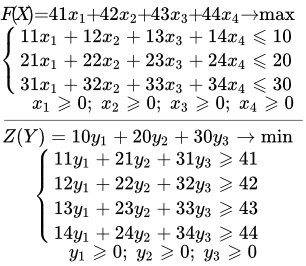Представлены правила составления двойственных задач. Рассмотрены симметричные, несимметричные и смешанные пары. Разобраны примеры составления двойственных задач. Решение двойственной задачи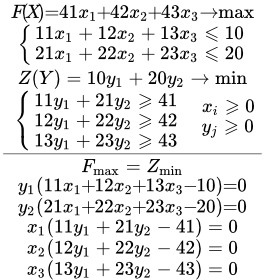Приводятся формулировки первой и второй теорем двойственности. Показано, как получить решение двойственной задачи из решения прямой, применяя эти теоремы. Подробно разобраны примеры решений задач. Онлайн калькулятор для составления и решения двойственной задачиОнлайн калькулятор позволяет к исходной задаче линейного программирования составить двойственную задачу, и решить обе задачи. Симплексный метод
Решение задач симплекс методом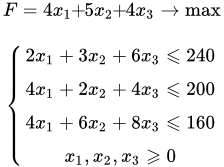
Рассмотрено решение задач линейного программирования симплекс методом. Рассмотрена двойственная задача и ее решение симплекс методом. Дан экономический смысл исходной задачи и переменных двойственной задачи. Рассмотрено решение задачи симплексным М – методом. Решение задач симплекс методом – онлайн калькулятор
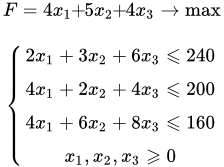Онлайн калькулятор для решения задачи симплекс методом. Первый опорный план можно рассчитать тремя способами: методом искусственного базиса (М-метод), двухшаговым или базовым методами. Ввод данных расчета возможен в виде обыкновенных или десятичных дробей. Пример решения прямой и двойственной задачи симплекс методомРассмотрен пример решения задачи симплекс методом, а также пример решения двойственной задачи. Пример решения задачи симплекс М-методом
Рассмотрен пример решения задачи, в которой начальный базис находится симплекс М методом. Пример отсутствия решения задачи, решаемой симплекс методом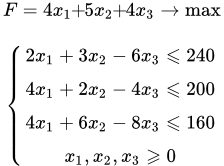
Рассмотрен пример решения задачи симплекс методом, в которой отсутствует решение - целевая функция может принимать сколь угодно большое значение.
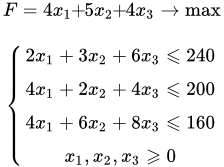Рассмотрено решение задач линейного программирования симплекс методом. Рассмотрена двойственная задача и ее решение симплекс методом. Дан экономический смысл исходной задачи и переменных двойственной задачи. Рассмотрено решение задачи симплексным М – методом. Решение задач симплекс методом – онлайн калькуляторОнлайн калькулятор для решения задачи симплекс методом. Первый опорный план можно рассчитать тремя способами: методом искусственного базиса (М-метод), двухшаговым или базовым методами. Ввод данных расчета возможен в виде обыкновенных или десятичных дробей. 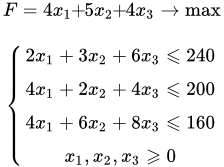Пример решения прямой и двойственной задачи симплекс методомРассмотрен пример решения задачи симплекс методом, а также пример решения двойственной задачи. Пример решения задачи симплекс М-методомРассмотрен пример решения задачи, в которой начальный базис находится симплекс М методом. Пример отсутствия решения задачи, решаемой симплекс методом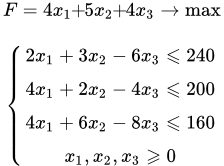Рассмотрен пример решения задачи симплекс методом, в которой отсутствует решение - целевая функция может принимать сколь угодно большое значение. Транспортная задача
Транспортная задача – основные понятия, определения и теоремы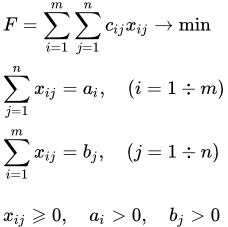
Основные понятия, определения и теоремы, относящиеся к транспортной задаче линейного программирования. Рассмотрены следующие вопросы: математическая модель транспортной задачи, открытия и закрытая модели, построение первого опорного плана методами северо-западного угла и наименьшей стоимости, переход от одного опорного плана к другому с помощью цикла, оценки свободных клеток и выбор новых базисных переменных методом потенциалов, множественность решения. Пример решения транспортной задачи методом потенциалов
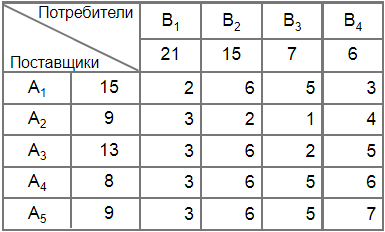Пример подробного решения транспортной задачи методом потенциалов. В задаче с неправильным балансом, открытая модель приводится к закрытой. Первый опорный план строится методом наименьшей стоимости. Задача решается методом потенциалов. Рассмотрена проблема зацикливания при вырожденном плане. Задача имеет не единственное решение. Приводятся несколько альтернативных опорных планов. Решение транспортной задачи – онлайн калькулятор
Онлайн калькулятор для решения транспортной задачи методом потенциалов. Расчет первого опорного плана осуществляется методом наименьшей стоимости или методом северо-западного угла. Решение выполняется как для закрытой, так и для открытой модели. Теорема о ранге матрицы системы ограничений транспортной задачи
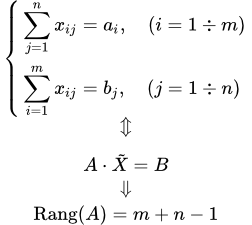Доказана теорема, согласно которой ранг матрицы коэффициентов системы ограничений транспортной задачи равен сумме числа поставщиков и потребителей минус один. Доказательство выполняется приведением матрицы к диагональному виду с помощью преобразований Жордана-Гаусса. Рассмотрено условие совместности системы уравнений транспортной задачи. Теорема о существовании решения транспортной задачи
Доказана теорема существования решения транспортной задачи. Решение транспортной задачи существует тогда и только тогда, когда суммарные запасы поставщиков равны суммарным потребностям потребителей.
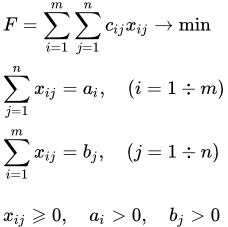Основные понятия, определения и теоремы, относящиеся к транспортной задаче линейного программирования. Рассмотрены следующие вопросы: математическая модель транспортной задачи, открытия и закрытая модели, построение первого опорного плана методами северо-западного угла и наименьшей стоимости, переход от одного опорного плана к другому с помощью цикла, оценки свободных клеток и выбор новых базисных переменных методом потенциалов, множественность решения. Пример решения транспортной задачи методом потенциаловПример подробного решения транспортной задачи методом потенциалов. В задаче с неправильным балансом, открытая модель приводится к закрытой. Первый опорный план строится методом наименьшей стоимости. Задача решается методом потенциалов. Рассмотрена проблема зацикливания при вырожденном плане. Задача имеет не единственное решение. Приводятся несколько альтернативных опорных планов. Решение транспортной задачи – онлайн калькуляторОнлайн калькулятор для решения транспортной задачи методом потенциалов. Расчет первого опорного плана осуществляется методом наименьшей стоимости или методом северо-западного угла. Решение выполняется как для закрытой, так и для открытой модели. Теорема о ранге матрицы системы ограничений транспортной задачи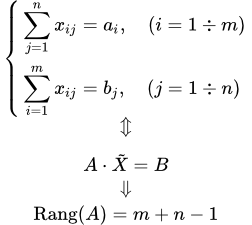Доказана теорема, согласно которой ранг матрицы коэффициентов системы ограничений транспортной задачи равен сумме числа поставщиков и потребителей минус один. Доказательство выполняется приведением матрицы к диагональному виду с помощью преобразований Жордана-Гаусса. Рассмотрено условие совместности системы уравнений транспортной задачи. Теорема о существовании решения транспортной задачиДоказана теорема существования решения транспортной задачи. Решение транспортной задачи существует тогда и только тогда, когда суммарные запасы поставщиков равны суммарным потребностям потребителей.