Методы решения физико-математических задач

Калькулятор сложения, вычитания, умножения и деления дробей

Пример деления и умножения дробей.
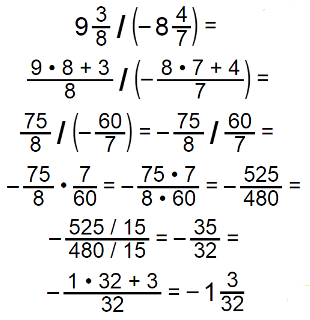
Онлайн калькулятор сложения, вычитания, умножения и деления дробей. Калькулятор использует длинную арифметику, и работает с большими числами.
Содержание
См. также:

Онлайн калькулятор

Введите дроби и выберите операцию сложения, вычитания, умножения или деления   ?






=



   

Краткое решение задачи

938 • 847 = 9 • 8 + 38 • 8 • 7 + 47 = 758 • 607 = 75 • 608 • 7 = 450056 = 4500 / 456 / 4 = 112514 = 80 • 14 + 514 = 80514 .

Ответ

938 • 847 = 80514 .

Подробное решение

  1. Переводим смешанные дроби в простые.
    938 = 9 + 38 = 9 • 88 + 38 = 9 • 8 + 38 = 72 + 38 = 758 .

    847 = 8 + 47 = 8 • 77 + 47 = 8 • 7 + 47 = 56 + 47 = 607 .
  2. Умножаем дроби, перемножая их числители и знаменатели.
    938 • 847 = 758 • 607 = 75 • 608 • 7 = 450056 .
  3. Проверим, нельзя ли сократить дробь. Для этого найдем наибольший общий делитель (НОД) числителя и знаменателя.
    НОД( 4500, 56 ) = 4
    См. Вычисление НОД этих чисел двумя способами с подробными объяснениями.
    Дроби можно сократить. Делим числитель и знаменатель на НОД.
    450056 = 4500 / 456 / 4 = 112514 .
  4. Переводим простую дробь в смешанную.
    112514 = 80 • 14 + 514 = 80 • 1414 + 514 = 80 + 514 = 80514 .

Ответ

938 • 847 = 80514 .

Описание калькулятора

  1. В поля ввода введите целую часть, числитель и знаменатель первой дроби.
  2. Из выпадающего списка выберите операцию сложения, вычитания, умножения или деления.
  3. Введите данные второй дроби.
  4. Если нужно изменить знак введенного числа, нажмите кнопку «+/–».
  5. Если заданы только простые дроби (без целой части), и результат вычислений нужно представить только в виде простой дроби, то нажмите переключатель «Простые дроби».
  6. Нажмите кнопку «Сложить (Вычесть, Умножить, Разделить) дроби».
  7. В результате появится краткое и подробное решение примера.

Калькулятор использует длинную арифметику и позволяет работать с большими числами.

Справочные данные

Натуральное число
– это одно из чисел множества , используемых для счета.
Обыкновенная дробь
– это форма записи числа в виде дроби , состоящая из числителя и знаменателя , которые являются натуральными числами . Как правило, обыкновенную дробь называют просто дробью, опуская слово “обыкновенная”. Число, представленное дробью является результатом деления числителя на знаменатель . Натуральное число также можно записать в виде обыкновенной дроби, знаменатель которой равен единице: .
Дробь может быть положительной: , и отрицательной: .
Правильная дробь
– это дробь , у которой числитель меньше знаменателя:
, где .
Неправильная дробь
– это дробь, у которой числитель больше знаменателя, или равен ему.
Смешанная дробь
– это форма записи неправильной дроби, состоящая из целого числа и правильной дроби . Смешанная дробь записывается так: . Она равна сумме целой части и правильной дроби:
.
Сокращение дроби
– это деление числителя и знаменателя дроби на их общий делитель, отличный от единицы.
Несократимая дробь
– это дробь, числитель и знаменатель которой не имеют общего делителя, кроме единицы.
Общий делитель чисел p и q
– это натуральное число , на которое делятся без остатка натуральные числа и :
– целое; – целое.
Наибольший общий делитель чисел p и q
– это наибольшее натуральное число , на которое делятся без остатка натуральные числа и :
– целое; – целое.
Общее кратное чисел p и q
– это натуральное число , которое делится без остатка на натуральные числа и :
– целое; – целое.
Наименьшее общее кратное чисел p и q
– это наименьшее натуральное число , которое делится без остатка на натуральные числа и :
– целое; – целое.
Представление натурального числа дробью
Натуральное число
можно представить в виде простой дроби, знаменатель которой равен единице:
.
Сложение простых дробей
Чтобы сложить простые дроби и   с равными знаменателями,
нужно сложить их числители:
.
Чтобы сложить простые дроби и   с разными знаменателями,
нужно привести их к общему знаменателю и сложить числители.
В качестве общего знаменателя можно использовать произведение знаменателей:
.
Также можно использовать наименьшее общее кратное знаменателей:
.
Вычитание простых дробей
Для вычитания дробей, нужно знак минус перед дробью перенести в числитель:
.
Затем выполнить сложение дробей.
.
Сложение смешанных дробей
Чтобы сложить смешанные дроби и ,
нужно сложить их целые и дробные части:
.
Если числитель дробной части окажется больше знаменателя или равным ему, то нужно перевести дробную часть в смешанную. В конце расчета, сумму целого числа и правильной дроби заменить смешанной дробью:
.
Вычитание дробей
Чтобы из дроби вычесть дробь ,
нужно знак минус перенести в целую часть и числитель, и сложить дроби, одна из которых будет иметь отрицательную целую часть и отрицательный числитель:
.
Или более кратко:
.
Если, в результате, знак целой части окажется противоположным знаку дробной части, то нужно выполнить дополнительное преобразование подобно этому:

.
Умножение дробей
Чтобы умножить простую дробь на дробь ,
нужно перемножить их числители и знаменатели:
.
Деление дробей
Чтобы разделить простую дробь на дробь ,
нужно умножить на :
.
Перевод смешанной дроби в простую
Чтобы перевести смешанную дробь в простую,
нужно к целой части прибавить дробную:
.
Перевод простой дроби в смешанную
Чтобы перевести простую дробь в смешанную ,
нужно разделить с остатком натуральное число на натуральное число . В результате мы получим неполное частное и остаток . Тогда число можно представить так:
.
Неполное частное будет целой частью смешанного числа; остаток от деления – числителем дробной части:
.

Автор: Олег Одинцов.     Опубликовано:

См. также:
▲
Меню