Пример отсутствия решения задачи, решаемой симплекс методом

Рассмотрен пример решения задачи симплекс методом, в которой отсутствует решение - целевая функция может принимать сколь угодно большое значение.

Содержание

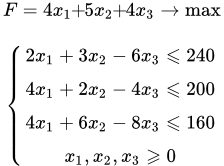
Условие задачи

Математическая модель задачи:

F = 4·x₁ + 5·x₂ + 4·x₃ –>max

Решаем симплекс методом.
Вводим дополнительные переменные x₄ ≥ 0, x₅ ≥ 0, x₆ ≥ 0, чтобы неравенства преобразовать в равенства.

В качестве базиса возьмем x₄ = 240; x₅ = 200; x₆ = 160.
Данные заносим в симплекс таблицу

Симплекс таблица № 1

$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline&C_i & & 4 & 5 & 4 & 0 & 0 & 0\\ \hline C_i&b_i & &x_1&x_2&x_3&x_4&x_5&x_6&Q\\ \hline 0 & x_4 & 240 & 2&3 & { \kern-0.2em-\kern-0.2em 6} & 1 & 0 & 0&80 \\ \hline0 & x_5 & 200 & 4&2 & { \kern-0.2em-\kern-0.2em 4} & 0 & 1 & 0&100 \\ \hline0 & x_6 & 160 & 4&\underline{6} & { \kern-0.2em-\kern-0.2em 8} & 0 & 0 & 1&\underline{26.667} \\ \hline & \Delta_i &0&{ \kern-0.2em-\kern-0.2em 4}&\underline{{ \kern-0.2em-\kern-0.2em 5}}&{ \kern-0.2em-\kern-0.2em 4}&0&0&0&\\ \hline\end{array}$

Целевая функция:

Вычисляем оценки по формуле:
.

Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:
Δ₂ = – 5

Вводим переменную x₂ в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение для столбца x₂:

= 26.667
Наименьшее неотрицательное: Q₃ = 26.667. Выводим переменную x₆ из базиса.
3-ю строку делим на 6.
Из 1-й строки вычитаем 3-ю строку, умноженную на 3
Из 2-й строки вычитаем 3-ю строку, умноженную на 2
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline&C_i & & 4 & 5 & 4 & 0 & 0 & 0\\ \hline C_i&b_i & &x_1&x_2&x_3&x_4&x_5&x_6&Q\\ \hline 0 & x_4 & \kern-0.3em 240\kern-0.3em-\kern-0.3em 3\kern-0.2em\cdot\kern-0.2em \frac{80}{3}\kern-0.3em & \kern-0.3em 2\kern-0.3em-\kern-0.3em 3\kern-0.2em\cdot\kern-0.2em \frac{2}{3}\kern-0.3em & \kern-0.3em 3\kern-0.3em-\kern-0.3em 3\kern-0.2em\cdot\kern-0.2em 1\kern-0.3em & \kern-0.3em { \kern-0.2em-\kern-0.2em 6}\kern-0.3em-\kern-0.3em 3\kern-0.2em\cdot\kern-0.2em \left(-\frac{4}{3}\right)\kern-0.3em & \kern-0.3em 1\kern-0.3em-\kern-0.3em 3\kern-0.2em\cdot\kern-0.2em 0\kern-0.3em & \kern-0.3em 0\kern-0.3em-\kern-0.3em 3\kern-0.2em\cdot\kern-0.2em 0\kern-0.3em & \kern-0.3em 0\kern-0.3em-\kern-0.3em 3\kern-0.2em\cdot\kern-0.2em \frac{1}{6}\kern-0.3em & \\ \hline0 & x_5 & \kern-0.3em 200\kern-0.3em-\kern-0.3em 2\kern-0.2em\cdot\kern-0.2em \frac{80}{3}\kern-0.3em & \kern-0.3em 4\kern-0.3em-\kern-0.3em 2\kern-0.2em\cdot\kern-0.2em \frac{2}{3}\kern-0.3em & \kern-0.3em 2\kern-0.3em-\kern-0.3em 2\kern-0.2em\cdot\kern-0.2em 1\kern-0.3em & \kern-0.3em { \kern-0.2em-\kern-0.2em 4}\kern-0.3em-\kern-0.3em 2\kern-0.2em\cdot\kern-0.2em \left(-\frac{4}{3}\right)\kern-0.3em & \kern-0.3em 0\kern-0.3em-\kern-0.3em 2\kern-0.2em\cdot\kern-0.2em 0\kern-0.3em & \kern-0.3em 1\kern-0.3em-\kern-0.3em 2\kern-0.2em\cdot\kern-0.2em 0\kern-0.3em & \kern-0.3em 0\kern-0.3em-\kern-0.3em 2\kern-0.2em\cdot\kern-0.2em \frac{1}{6}\kern-0.3em & \\ \hline5 & x_2 & \frac{80}{3} & \frac{2}{3} & 1 & { \kern-0.2em-\kern-0.2em \frac{4}{3}} & 0 & 0 & \frac{1}{6}& \\ \hline\end{array}$

Вычисляем:

Получаем новую таблицу.

Симплекс таблица № 2

$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline&C_i & & 4 & 5 & 4 & 0 & 0 & 0\\ \hline C_i&b_i & &x_1&x_2&x_3&x_4&x_5&x_6&Q\\ \hline 0 & x_4 & 160 & 0 & 0&{ \kern-0.2em-\kern-0.2em 2} & 1 & 0 & { \kern-0.2em-\kern-0.2em \frac{1}{2}}&- \\ \hline0 & x_5 & \frac{440}{3} & \frac{8}{3} & 0&{ \kern-0.2em-\kern-0.2em \frac{4}{3}} & 0 & 1 & { \kern-0.2em-\kern-0.2em \frac{1}{3}}&- \\ \hline5 & x_2 & \frac{80}{3} & \frac{2}{3} & 1&{ \kern-0.2em-\kern-0.2em \frac{4}{3}} & 0 & 0 & \frac{1}{6}&- \\ \hline & \Delta_i &\frac{400}{3}&{ \kern-0.2em-\kern-0.2em \frac{2}{3}}&0&\underline{{ \kern-0.2em-\kern-0.2em \frac{32}{3}}}&0&0&\frac{5}{6}&\\ \hline\end{array}$

Целевая функция:

Вычисляем оценки по формуле:
.

Поскольку есть отрицательные оценки, то план не оптимален. Наименьшая оценка:
Δ₃ = – 32/3

Вводим переменную x₃ в базис.
Определяем переменную, выходящую из базиса. Для этого находим наименьшее неотрицательное отношение для столбца x₃:
< 0
< 0
< 0

Поскольку среди значений нет неотрицательных, то решения не существует. Целевая функция может быть сделана сколь угодно большой.

Ответ

Решения задачи не существует. Целевая функция может быть сколь угодно большой.

Автор: Олег Одинцов. Опубликовано: 08-12-2011