Кинематический анализ плоского механизма – пример решения задачи
Основные законы и формулы, применяемые при решении задач
Использование мгновенного центра скоростей
При плоском движении твердого тела, отличном от поступательного, существует такая точка, скорость которой равна нулю. Такая точка называется мгновенным центром скоростей (МЦС) тела. Точка МЦС может как принадлежать телу, так и находиться за его пределами. Положение мгновенного центра скоростей может как оставаться неизменным, так и меняться в течении времени.
Если положение МЦС остается неизменным, то такое движение называется вращением вокруг неподвижной оси. В этом случае точка мгновенного центра скоростей совпадает с осью вращения, направленной перпендикулярной плоскости движения. Все необходимые для этого случая формулы даны на странице «Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях».
Но даже если положение МЦС меняется со временем, то формулы для определения скоростей точек тела имеют тот же вид, что и при вращении вокруг неподвижной оси, проходящей через мгновенный центр скоростей. Для ускорений такой подход не работает, но скорости точек можно определять по формулам вращательного движения с неподвижной осью.
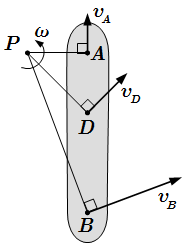
Для определения положения МЦС мы используем свойство вращательного движения: направление скорости любой точки тела перпендикулярно прямой, проведенной через эту точку и центр вращения. Здесь мы изначально принимаем, что движение является плоским. То есть центр вращения является осью, перпендикулярной плоскости движения. Если мы знаем направления скоростей и двух точек A и B, то мы можем определить положение МЦС. Для этого надо через эти точки провести прямые, перпендикулярные векторам и . Точка P пересечения этих прямых и является мгновенным центром скоростей. Если эти прямые не пересекаются, то это поступательное движение. В этом случае скорости всех точек тела равны. Если же прямые совпадают, то зная только направления скоростей выбранных точек, определить положение МЦС нельзя.
Зная положение МЦС и абсолютное значение скорости хотя бы одной точки тела, мы можем определить угловую скорость ω и скорости всех точек тела в рассматриваемый момент времени. Для этого мы применяем следующую формулу:
.
Здесь |DP| – расстояние между произвольной точкой D и мгновенным центром скоростей P. Вектор скорости направлен перпендикулярно DP.
Применение теоремы о проекции скоростей
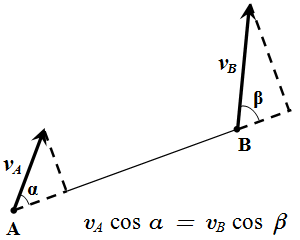
Пусть мы знаем направление и абсолютную величину скорости одной точки и направление другой точки тела. Тогда найти абсолютное значение второй точки можно с помощью теоремы о проекции скоростей:
.
Применение теоремы о скоростях точек плоской фигуры
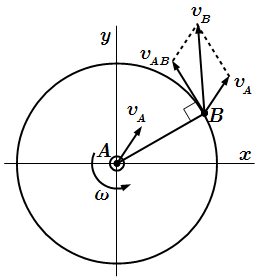
Согласно теореме о скоростях точек плоской фигуры, скорость произвольной точки B определяется по формуле:
(1) .
Здесь – скорость наперед выбранной точки тела, которую, в данном случае, называют полюсом; – скорость точки B относительно A.
Удобство применения этой теоремы состоит в том, что относительное движение является вращением вокруг неподвижной оси, проходящей через полюс A. Тогда относительная скорость определяется по формулам вращательного движения. То есть мы раскладываем движение на поступательное со скоростью и вращательное относительно центра A.
Вектор угловой скорости перпендикулярен плоскости движения. Поэтому он перпендикулярен AB (см. рисунок 3). Тогда относительная скорость направлена перпендикулярно отрезку AB в сторону вращения. Спроектировав векторное равенство (1) на ось AB, получим теорему о проекциях скоростей (см. рис. 2):
(2) .
Спроектировав (1) на ось, перпендикулярную AB, получим уравнение, связывающее скорости точек с угловой скоростью тела:
(3) .
Здесь следует выбрать знак плюс или минус исходя из направления вращения.
Применение теоремы об ускорениях точек плоской фигуры
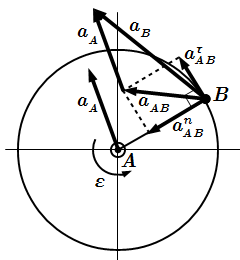
При вычислении ускорения мы также можем разложить движение на поступательное и вращательное. Согласно теореме об ускорениях точек плоской фигуры, ускорение произвольной точки B фигуры определяется по формуле:
(4)
.
Здесь – ускорение предварительно выбранной точки тела, которую называют полюсом; – ускорение точки B относительно точки A. Относительное движение является вращением вокруг неподвижной оси, проходящей через полюс A. К относительному ускорению применимы формулы вращения вокруг неподвижной оси. Тогда вектор можно разложить на касательное и нормальное ускорение:
.
Касательное относительное ускорение еще называют вращательным или тангенциальным ускорением. Оно определяется аналогично скорости точки, вращающейся вокруг неподвижного центра:
.
Только вместо угловой скорости здесь стоит угловое ускорение . Вектор направлен по касательной к траектории, то есть по касательной к окружности с центром в точке A и радиусом AB.
Нормальное относительное ускорение также называют центростремительным ускорением. Оно всегда направлено к центру вращения (нормально, то есть перпендикулярно траектории):
.
Пример решения задачи

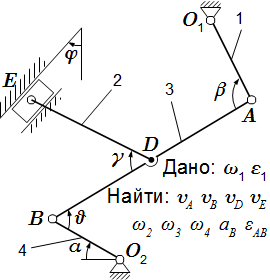
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна Е, соединенных друг с другом и с неподвижными опорами O1, О2 шарнирами. Точка D находится в середине стержня АВ. Длины стержней равны соответственно: l1 = 0,4 м, l2 = 1,2 м, l3 = 1,4 м, l4 = 0,6 м. Взаимное расположение элементов механизма определяется углами: α = 90°, β = 120°, γ = 150°, φ = 0°, θ = 30°. Задана угловая скорость и угловое ускорение звена 1: ω1 = 5 c–1, ε1 = 10 c–2. Угловая скорость направлена против часовой стрелки; угловое ускорение – в противоположную сторону.
Определить скорости точек A, B, D, E; угловые скорости звеньев 2, 3, 4; ускорение точки B и угловое ускорение звена 3.
Указания. Эта задача – на анализ и исследование кинематики плоского механизма. При ее решении, для определения скоростей точек и угловых скоростей звеньев, следует воспользоваться понятием о мгновенном центре скоростей и теоремой о проекциях скоростей двух точек тела. При определении ускорения точки В звена АВ, применить теорему об ускорении точек плоской фигуры.
Дано:
ω1 = 5 c–1, ε1 = 10 c–2, l1 = 0,4 м, l2 = 1,2 м, l3 = 1,4 м, l4 = 0,6 м, α = 90°, β = 120°, γ = 150°, φ = 0°, θ = 30°.
Решение
Определение скоростей с помощью мгновенного центра скоростей
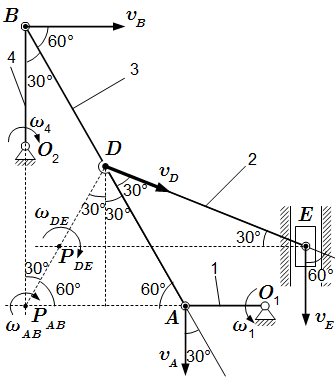
Делаем рисунок механизма при заданных значениях углов.
Точка A вращается вокруг неподвижного центра O1 с заданной угловой скоростью ω1 = 5 c–1 против часовой стрелки. Поэтому скорость точки A направлена перпендикулярно вниз, и имеет абсолютную величину
м/с.
Найдем мгновенный центр скоростей (МЦС) звена AB. Для этого воспользуемся свойством, согласно которому, скорость произвольной точки твердого тела перпендикулярна прямой, проведенной через эту точку и мгновенный центр скоростей. Тогда, чтобы найти МЦС, нужно знать направления скоростей двух точек тела.
Нам известно направление скорости точки A. Далее замечаем, что точка B вращается вокруг неподвижного центра O2. Поэтому скорость этой точки перпендикулярна отрезку O2B. Изображаем вектор скорости на рисунке. Определяем МЦС. Для этого через точки A и B проводим прямые, перпендикулярные векторам и . Они пересекаются в точке, которую обозначим как PAB. Эта точка и является мгновенным центром скоростей звена AB.
Из геометрического построения получаем, что треугольник ABPAB – прямоугольный. Находим длины его сторон:
м;
м.
Используя формулу , находим угловую скорость вращения звена AB:
с–1.
Находим абсолютную величину скорости точки B:
м/с.
Найдем скорость точки D учитывая, что она принадлежит звену AB, угловую скорость которого и положение мгновенного центра скоростей мы знаем. Соединяем точки D и PAB отрезком. Из геометрического построения получаем, что треугольник DAPAB – равносторонний. Тогда
м.
Модуль скорости точки D:
м/с.
Направление скорости перпендикулярно отрезку DPAB. В нашей задаче получается, что скорость направлена вдоль звена DE.
Теперь рассмотрим звено DE. Направление скорости точки D мы уже знаем. Направление движения точки E задается направляющими, то есть, в нашем случае, вертикально. Через точки D и E проводим прямые, перпендикулярные векторам и . Точка пересечения этих прямых является мгновенным центром скоростей PDE звена DE.
Из построения находим, что в треугольнике EDPDE, угол , . Тогда
м;
м.
Угловая скорость звена DE:
с–1.
Скорость точки E:
м/с.
Точка B вращается вокруг неподвижного центра O2. Зная скорость этой точки, находим угловую скорость вращения звена 4:
с–1.
Определение скоростей с помощью теоремы о проекциях скоростей и теоремы о скоростях точек плоской фигуры
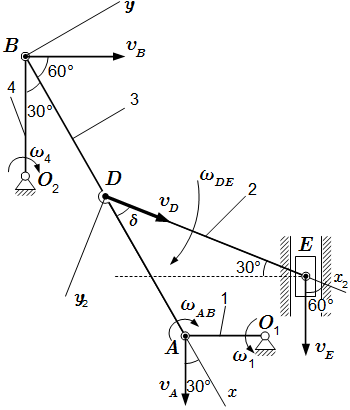
Теперь найдем значения скоростей, используя теорему о проекциях скоростей двух точек твердого тела на соединяющих их прямую. и теорему о скоростях точек плоской фигуры. Вычисляем скорость точки A.
м/с.
Применим теорему о проекциях скоростей. Из построения, угол между вектором и осью BA равен 60°. Угол между вектором скорости и той же осью равен 30°. По этой теореме, проекции скоростей двух точек твердого тела на прямую, проведенную через эти точки равны:
.
Отсюда м/с.
Найдем угловую скорость звена AB, применяя теорему о скоростях точек плоской фигуры: .
Направим ось x вдоль AB, ось y – перпендикулярно (см. рисунок 7). Спроектируем это векторное уравнение на ось y:
;
с–1.
Найдем скорость точки D. Применим теорему о скоростях точек плоской фигуры:
(П1) .
Пусть δ – угол между осью x и вектором скорости . Относительная скорость направлена по оси y и по модулю равна м/с.
Спроектируем векторное уравнение (П1) на оси x и y:
м/с;
м/с.
Отсюда
м/с;
.
Мы нашли . То есть вектор направлен вдоль звена 2.
Применим теорему о проекциях скоростей для звена 2. Векторы скоростей и составляют углы 0° и 60° с прямой DE. Тогда
;
м/с.
Найдем угловую скорость звена DE, применяя теорему о скоростях точек плоской фигуры. В качестве полюса возьмем точку D.
.
Спроектируем это векторное уравнение на ось y2, перпендикулярную DE (см. рисунок 7):
;
с–1.
Находим угловую скорость вращения звена 4:
с–1.
Определение ускорений
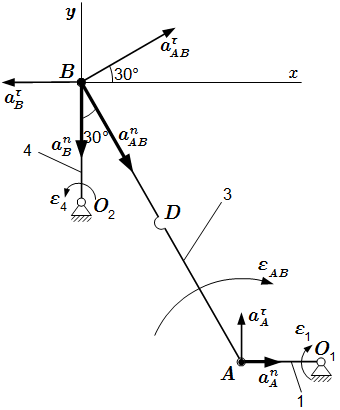
Точка A движется по окружности радиуса O1A = l1. Найдем ее ускорение учитывая, что движение является вращением вокруг неподвижной оси.
.
Касательное ускорение направлено по касательной к траектории, то есть по касательной к дуге окружности радиуса |O1A| с центром в точке O1. Направление задается направлением углового ускорения ε1. В нашем случае, оно направлено вверх и имеет абсолютную величину
м/с2.
Нормальное ускорение направлено к центру вращения и имеет абсолютную величину
м/с2.
Применим теорему об ускорениях точек плоской фигуры. В качестве полюса возьмем точку A. Тогда для ускорения точки B имеем:
.
Подставим .
(У1) .
Здесь нормальное ускорение точки B относительно точки A. Относительное движение является вращением вокруг неподвижной оси, проходящей через точку A перпендикулярно плоскости рисунка. Поскольку угловая скорость звена AB известна, то м/с2.
Вектор направлен к оси вращения. В нашем случае – от B к A.
– касательное ускорение при движении точки B относительно A. Оно перпендикулярно AB и имеет абсолютную величину
.
Угловое ускорение εAB звена AB нам не известно. Выберем его направление произвольным образом. Будем считать, что оно направлено по часовой стрелке. Если оно будет направлено в противоположную сторону, то для εAB получим отрицательное значение. Изображаем векторы и на рисунке. Для удобства откладываем их из точки B.
С другой стороны, точка B вращается вокруг неподвижного центра O2. Для вращения вокруг неподвижной оси имеем:
(У2) .
Здесь – нормальное ускорение. Оно направлено от B к O2. Зная угловую скорость вращения звена 4, найдем его абсолютную величину.
м/с2.
– касательное ускорение точки B при вращении относительно неподвижного центра O2. Оно направлено по касательной к окружности и по абсолютной величине равно
.
Здесь – угловое ускорение звена 4. Считаем, что оно направлено против часовой стрелки. Изображаем векторы и на рисунке.
Итак, для ускорения точки B мы получили два уравнения.
(У1) .
(У2) .
Отсюда
(У3) .
Проводим оси системы координат. Ось x направим горизонтально, ось y – вертикально. Спроектируем векторное уравнение (У3) на ось y.
;
.
Отсюда
м/с2;
с–2.
Спроектируем уравнение (У3) на ось x.
;
.
Отсюда
м/с2.
Полное ускорение точки B.
м/с2.
Ответ
м/с; м/с; м/с; м/с; с–1; с–1; с–1; с–2; м/с2.
Автор: Олег Одинцов. Опубликовано:
