Естественный способ задания движения точки
Введение
Естественный способ задания движения материальной точки применяется в тех случаях, когда траектория заранее известна. Например, точка движется внутри желоба в твердом теле. В этом случае мы, произвольным образом, выбираем на траектории некоторую неподвижную точку , которую принимаем за начало отсчета. Далее мы произвольным образом выбираем положительное направление. Рассмотрим подвижную точку . Пусть – расстояние от начала отсчета до , измеренное вдоль дуги траектории. Введем криволинейную координату следующим образом. Если точка находится в положительном направлении относительно начала отсчета , то . Если в отрицательном, то . Тогда криволинейная координата однозначно определяет положение точки на траектории. При движении, координата изменяется со временем :
.
Таким образом, при естественном способе задания движения материальной точки, мы задаем следующие данные:
1) траекторию точки;
2) начало отсчета с указанием положительного и отрицательного направления отсчета;
3) криволинейную координату, как функцию от времени: .
Определение кинематических величин
Вначале мы должны определить геометрические характеристики траектории – касательную, главную нормаль и радиус кривизны.
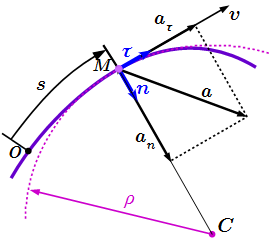
По заданной траектории, для любого положения точки, мы можем определить единичный вектор , направленный по касательной к траектории; единичный вектор , направленный вдоль главной нормали (к центру кривизны) и радиус кривизны траектории. Поскольку вектор можно направить по касательной двумя взаимно противоположными способами, то мы направим вектор вдоль направления, которое мы приняли за положительное. Вектор можно направить только одним способом – к центру кривизны траектории. Векторы и представляют собой два орта естественного трехгранника. В простых случаях, найти векторы , и радиус кривизны можно геометрическим способом (см. пример решения задачи ниже). Как найти эти величины в более сложных случаях, указано на странице “Оси естественного трехгранника”. Там же приводится пример определения векторов , и радиуса кривизны траектории для винтовой линии.

После того, как мы определили орты естественного трехгранника , и радиус кривизны траектории , мы можем найти векторы скорости и ускорения точки . Выводы представленных ниже формул даны на странице “Кинематика материальной точки”.
Дифференцируя по , находим проекцию скорости на вектор :
.
Модуль скорости:
.
Вектор скорости:
.
Скорость, как и следовало, направлена по касательной к траектории. Если скорость направлена в положительном направлении, то
.
Если скорость направлена в отрицательном направлении, то
.
Дифференцируя по , находим тангенциальное ускорение (проекцию ускорения на вектор ):
.
Вектор тангенциального ускорения:
.
Нормальное ускорение:
.
Вектор нормального ускорения:
.
Вектор полного ускорения:
.
Модуль полного ускорения:
.
Пример решения задачи
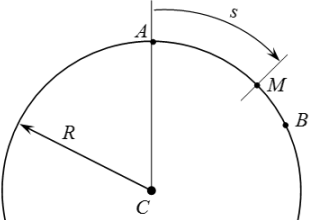
Точка движется по дуге окружности радиуса по закону
(s – в метрах, t – в секундах), где – расстояние от до , измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени . Изобразить на рисунке векторы и , считая, что точка в этот момент находится в положении , а положительное направление отсчета – от к .
Решение
Определим положение точки в момент времени .
.
Пусть – центр окружности. Угол между векторами и :
.
По условию, положительное направление – от к , то есть слева направо. Поскольку , то точка расположена слева от точки .
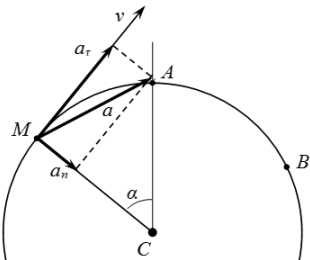
Дифференцируя по , находим проекцию скорости на направление касательной к траектории:
.
В момент времени :
.
Поскольку , то вектор скорости направлен по касательной к траектории в сторону возрастания . Абсолютное значение (модуль) скорости:
.
Дифференцируя по , находим касательное ускорение точки:
.
В момент времени :
.
Поскольку , то вектор касательного ускорения направлен по касательной к траектории в сторону возрастания .
Нормальное ускорение:
.
Вектор направлен к центру окружности.
Полное ускорение:
.
Ответ
;
.
Автор: Олег Одинцов. Опубликовано:
