Скорость и ускорение точек твердого тела, совершающего поступательное и вращательное движения
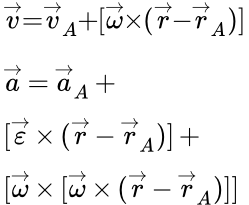
Основные формулы
Скорость и ускорение точки твердого тела с радиус вектором определяются по формулам:
;
.
где – угловая скорость вращения, – угловое ускорение. Они равны для всех точек тела и могут изменяться со временем t.
и – скорость и ускорение произвольным образом выбранной точки A с радиус вектором . Такую точку часто называют полюсом.
Здесь и далее, произведения векторов в квадратных скобках означают векторные произведения.
Далее мы приводим вывод этих формул исходя из того, что при движении твердого тела, расстояние между двумя любыми его точками остается постоянным.
Вывод формулы для скорости
Выберем прямоугольную неподвижную систему координат Oxyz. Возьмем две произвольные точки твердого тела A и B. Пусть (xA, yA, zA) и (xB, yB, zB) – координаты этих точек. При движении твердого тела они являются функциями от времени t. Их производные по времени t являются проекциями скоростей точек:
, .
Воспользуемся тем, что при движении твердого тела, расстояние |AB| между точками остается постоянным, то есть не изменяется со временем t. Также постоянным является квадрат расстояния
.
Продифференцируем это уравнение по времени t, применяя правило дифференцирования сложной функции.
Сократим на 2.
(1)
Введем векторы
,
.
Тогда уравнение (1) можно представить в виде скалярного произведения векторов:
(2) .
Отсюда следует, что вектор перпендикулярен вектору . Воспользуемся свойством векторного произведения. Тогда можно представить в виде:
(3) .
где – некоторый вектор, который мы вводим только для того, чтобы автоматически выполнялось условие (2).
Запишем (3) в виде:
(4) ,
Теперь займемся изучением свойств вектора . Для этого составим уравнение, которое не содержит скоростей точек. Возьмем три произвольные точки твердого тела A, B и C. Запишем для каждой пары этих точек уравнение (4):
;
;
.
Сложим эти уравнения:
.
Сокращаем сумму скоростей в левой и правой части. В результате получаем векторное уравнение, содержащее только исследуемые векторы :
(5) .
Легко заметить, что уравнение (5) имеет решение:
,
где – какой-то вектор, имеющий равное значение для любых пар точек твердого тела. Тогда уравнение (4) для скоростей точек тела примет вид:
(6) .
Теперь рассмотрим уравнение (5) с математической точки зрения. Если записать это векторное уравнение по компонентам на оси координат x, y, z, то векторное уравнение (5) является линейной системой, состоящей из 3-ех уравнений с 9-ю переменными:
ωBAx , ωBAy , ωBAz , ωCBx , ωCBy , ωCBz , ωACx , ωACy , ωACz .
Если уравнения системы (5) линейно не зависимы, то их общее решение содержит 9 – 3 = 6 произвольных постоянных. Поэтому мы нашли не все решения. Существуют еще какие-то. Чтобы их найти замечаем, что найденное нами решение полностью определяет вектор скорости . Поэтому дополнительные решения не должны приводить к изменению скорости. Заметим, что векторное произведение двух равных векторов равно нулю. Тогда, если в (6) к вектору прибавить член, пропорциональный , то скорость не изменится:
.
Тогда общее решение системы (5) имеет вид:
;
;
,
где CBA, CCB, CAC – постоянные.
Выпишем общее решение системы (5) в явном виде.
ωBAx = ωx + CBA(xB – xA)
ωBAy = ωy + CBA(yB – yA)
ωBAz = ωz + CBA(zB – zA)
ωCBx = ωx + CCB(xC – xB)
ωCBy = ωy + CCB(yC – yB)
ωCBz = ωz + CCB(zC – zB)
ωACx = ωx + CAC(xA – xC)
ωACy = ωy + CAC(yA – yC)
ωACz = ωz + CAC(zA – zC)
Это решение содержит 6 произвольных постоянных:
ωx, ωy, ωz, CBA, CCB, CAC.
Как и должно быть. Таким образом, мы нашли все члены общего решения системы (5).
Физический смысл вектора ω
Как уже указывалось, члены вида не влияют на значения скоростей точек. Поэтому их можно опустить. Тогда скорости точек твердого тела связаны соотношением:
(6) .
Выясним физический смысл вектора .
Для этого положим vA = 0. Это всегда можно сделать если выбрать систему отсчета, которая в рассматриваемый момент времени движется относительно неподвижной системы со скоростью . Начало системы отсчета O поместим в точку A. Тогда rA = 0. И формула (6) примет вид:
.
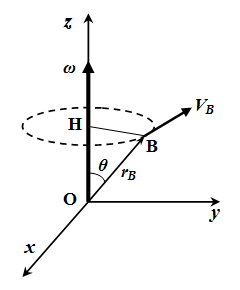
Ось z системы координат направим вдоль вектора .
По свойству векторного произведения, вектор скорости перпендикулярен векторам и . То есть он параллелен плоскости xy. Модуль вектора скорости:
vB = ω rB sin θ = ω |HB|,
где θ – это угол между векторами и ,
|HB| – это длина перпендикуляра, опущенного из точки B на ось z.
Если вектор не меняется со временем, то точка B движется по окружности радиуса |HB| со скоростью
vB = |HB| ω.
То есть ω – это угловая скорость вращения точки B вокруг точки H.
Таким образом, мы приходим к выводу, что – это вектор мгновенной угловой скорости вращения твердого тела.
Скорость точек твердого тела
Итак, мы нашли, что скорость произвольной точки B твердого тела определяется по формуле:
(6) .
Она равна сумме двух членов. Точку A часто называют полюсом. В качестве полюса обычно выбирают неподвижную точку или точку, совершающую движение с известной скоростью. Второй член представляет собой скорость вращения точек тела относительно полюса A.
Поскольку точка B – это произвольная точка, то в формуле (6) можно сделать подстановку . Тогда и скорость точки твердого тела с радиус вектором определяются по формуле:
.
Скорость произвольной точки твердого тела равна сумме скорости поступательного движения полюса A и скорости вращательного движения относительно полюса A.
Ускорение точек твердого тела
Теперь выведем формулу для ускорения точек твердого тела. Ускорение – это производная скорости по времени. Дифференцируем формулу для скорости
,
применяя правила дифференцирования суммы и произведения:
.
Вводим ускорение точки A
;
и угловое ускорение тела
.
Далее замечаем, что
.
Тогда
.
Или
.
То есть вектор ускорения точек твердого тела можно представить в виде суммы трех векторов:
,
где
– ускорение произвольно выбранной точки, которую часто называют полюсом;
– вращательное ускорение;
– осестремительное ускорение.
Если угловая скорость изменяется только по величине и не изменяется по направлению, то векторы угловой скорости и ускорения направлены вдоль одной прямой. Тогда направление вращательного ускорения совпадает или противоположно направлению скорости точки. Если угловая скорость изменяется по направлению, то вращательное ускорение и скорость могут иметь разные направления.
Осестремительное ускорение всегда направлено в сторону мгновенной оси вращения так, что пересекает ее под прямым углом.
Автор: Олег Одинцов. Опубликовано:
