Обыкновенные дроби. Математика 5 класс

Рассмотрено все, что нужно знать школьнику 5 класса об обыкновенных дробях.

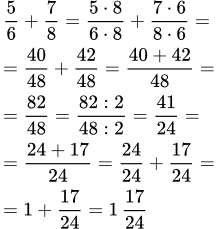
Основные правила действий с дробями

Разобраться с дробями довольно просто. Для этого нужно уяснить основные правила. Вот они.

• Обыкновенная дробь, или просто дробь записывается через черту. Над чертой числитель, под чертой знаменатель. Для обыкновенных дробей, которые изучаются в 5-м классе, числитель и знаменатель являются целыми числами. Вот примеры дробей:
  .
  Но вообще, в математике, числитель и знаменатель может быть любым числом или даже функцией. Но это уже для старших классов.
• Любое целое число можно преобразовать в дробь. В числителе ставим это число, в знаменателе единицу:
  .
• Числитель и знаменатель дроби можно умножать или делить на одно и то же число. Число может быть любым, кроме нуля. Это самое главное правило, которое нужно уяснить. С помощью этого правила выполняются основные действия с дробями. Примеры:
  ;
  ;
  .
• Чтобы умножить две дроби, нужно перемножить их числители и знаменатели:
  .
• Чтобы разделить дроби, нужно умножить числитель первой на знаменатель второй, и знаменатель первой на числитель второй:
  .
  Или можно заменить операцию деления умножением, перевернув вторую дробь:
  ;
  .
• Чтобы сложить две дроби, нужно сначала привести их к общему знаменателю. То есть преобразовать так, чтобы знаменатели оказались равными. После этого, сложить числители.
  Найдем сумму и . Сначала приводим дроби к общему знаменателю. Для этого умножаем числитель и знаменатель первой дроби на 5, а второй на 7. После этого складываем числители:
  .
• Чтобы из одной дроби вычесть другую, нужно, как и при сложении, привести их к общему знаменателю. После этого из числителя первой вычесть числитель второй. .
• Чтобы сравнить дроби, их нужно привести к общему знаменателю, и сравнить числители.
  Сравним дроби и . Приводим их к общему знаменателю:
  ,
  .
  Теперь сравниваем числители: . Тем самым мы нашли, что . Но поскольку , и , то
  .
• Если числитель и знаменатель дроби делятся на некоторое число без остатка, то такую дробь можно сократить, разделив числитель и знаменатель на это число. Такая дробь называется сократимой. Если нет такого числа, на которое числитель и знаменатель делятся без остатка, то ее называют несократимой дробью. Примеры сокращения дробей:
  ;
  .
  Здесь – сократимые дроби; – несократимые.
• Правильная дробь – это дробь, у которой числитель меньше знаменателя. Неправильная – у которой числитель больше или равен знаменателю. Например, – правильные дроби; – неправильные.
• Смешанная дробь – это форма записи неправильной дроби, состоящая из целого числа и правильной дроби. Например: . Смешанная дробь равна сумме целой и дробной частей. Во многих действиях, смешанные дроби удобнее сначала переводить в неправильные, и только потом выполнять арифметические операции. Пример перевода смешанной дроби в неправильную:
  .
• Противоположность смешанной дроби – обыкновенная дробь, или просто дробь, которая не имеет целой части, и записывается в виде . Обыкновенные дроби бывают правильные и неправильные. Неправильные можно перевести в смешанные.
• Операция деления тоже является дробью:
  .
  Иногда дробь записывают через косую черту:
  .
  С обозначениями может возникнуть путаница, например:
  .
  Здесь только более длинная средняя черта указывает, что это операция деления верхней дроби на нижнюю . Чтобы не вводить никого в заблуждение, для подобных случаях лучше использовать скобки:
  .
  Если не выделить среднюю черту, то получится другой результат:
  
  .

Важно уяснить эти правила, и научиться свободно складывать, умножать и делить дроби. Можно самостоятельно брать любые числа, составлять из них дроби и выполнять с ними арифметические операции. Для проверки результата можно использовать следующие калькуляторы:
Калькулятор сложения, вычитания, умножения и деления дробей
Калькулятор нахождения наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК)
Разложение числа на простые множители
Таблица простых чисел

Далее рассмотрены некоторые важные понятия и правила, используемые при работе с дробями.

Сокращение дробей

Если числитель и знаменатель дроби делятся на некоторое число без остатка, то такую дробь можно сократить, разделив числитель и знаменатель на это число. В результате получится более простая дробь, состоящая из меньшего количества цифр.

Для сокращения дроби, нужно последовательно пытаться разделить числитель и знаменатель на простые числа в порядке их возрастания: 2, 3, 5, 7, 11, 13, .... См. Таблица простых чисел
В качестве примера, попробуем сократить дробь .

Проверим, делятся ли числа 2520 и 14850 на 2. Признак делимости на 2 – число четное. У нас оба числа четные. Делим их на 2:
.
Полученную дробь снова попытемся разделить на 2. Но 2425 – число нечетное, поэтому не делится без остатка на 2. Значит на 2 больше сократить нельзя.

Следующее простое число 3. Проверим, делятся ли числа 1260 и 7425 на 3. Признак делимости на 3 – сумма цифр делится на 3. Первое число 1 + 2 + 6 + 0 = 9 делится на 3. Второе число 7 + 4 + 2 + 5 = 18 тоже делится на 3. Сокращаем на 3:
.
Снова попытемся разделить числитель и знаменатель на 3. Числитель 4 + 2 + 0 = 6 делится на 3. Знаменатель 2 + 4 + 7 + 5 = 18 тоже делится на 3. Еще раз сокращаем на 3:
.
Далее, числитель 1 + 4 + 0 = 5 на 3 не делится. Больше сокращать на 3 нельзя.

Следующее простое число 5. Попробуем сократить на него. Признак деления на 5 – число оканчивается на 5 или 0. Ему удовлетворяют и числитель 140 и знаменатель 825. Сокращаем на 5:
.
Поскольку 28 не оканчивается на 5 или 0, то оно не делится на 5. Сократить на 5 больше не получится.

Следующее простое число 7. Но 165 не делится на 7 без остатка. Поэтому на 7 сократить нельзя.

Следующее простое число 11. Но оно уже довольно большое. Поскольку 11·11 = 121 > 28, то на 11 и последующие простые числа сократить нельзя. В результате мы получили несократимую дробь .

Наибольший общий делитель

Выпишем полный процесс сокращения:
.
Найдем произведение всех делителей.
.
Тогда весь процесс сокращения можно записать одной строчкой:
.
В результате мы получили несократимую дробь . Число 90 называется наибольшим общим делителем чисел 2520 и 14850, и обозначается так: НОД(2520, 14850) = 90. Таким образом, чтобы из сократимой получить несократимую дробь, нужно числитель и знаменатель разделить на их наибольший общий делитель.

Приведение дробей к общему знаменателю

Простой способ

Пусть нам требуется привести к общему знаменателю дроби и . Самый простой способ – это взять произведение знаменателей исходных дробей. Для этого числитель и знаменатель первой дроби умножают на знаменатель второй, а числитель и знаменатель второй умножают на знаменатель первой дроби:
,
.
В качестве примера, приведем к общему знаменателю дроби и :
,
.

Но иногда можно сделать проще. Рассмотрим дроби и . Заметим, что . Умножив числитель и знаменатель первой дроби на 2, получим дроби, знаменатели которых равны:
,   и   .
В качестве общего знаменателя также можно взять произведение :
;
.

Наименьшее общее кратное

В предыдущем примере мы получили два варианта приведения дробей к общему знаменателю:
1)   ;
2)   .
Для вычислений можно пользоваться любым способом. В любом случае результат будет правильный. Но в первом случае дроби проще, общий знаменатель получился меньше. Он наименьший из всех возможных. Такой знаменатель называют наименьшим общим кратным чисел 11 и 22: НОК(11, 22) = 22. Наименьшее общее кратное чисел q и s это наименьшее число, на которое делятся без остатка и q и s. Его обозначают так: НОК(q, s).

Чтобы найти наименьшее общее кратное двух чисел, можно разложить их на простые множители, и взять произведения множителей, которые встречаются в обоих числах. Например, если , а , то .
То есть все множители, которые есть в q и s содержатся в НОК.

Есть и другой способ. Сначала нужно найти наименьший общий делитель чисел, а затем НОК по формуле:
.
Для предыдущего примера,
;
.

Смешанные дроби

Сравнение смешанных дробей

Смешанные дроби легче сравнивать, чем неправильные. Чтобы сравнить две смешанные дроби, надо сначала сравнить их целые части. Если они равны, то сравниваются дробные части.

Сравним смешанные дроби и . Сначала сравниваем целые части 2 и 3. Поскольку , то . То есть в этом случае нам не пришлось делать более трудоемкую задачу по сравнению дробных частей.

Теперь сравним дроби и . Сравниваем целые части. Поскольку они равны: , то нужно сравнить дробные части. Для этого приводим их к общему знаменателю:
,
.
Теперь сравниваем числители: . То есть . Поскольку и , то . Значит
.

Сложение смешанных дробей

Для сложения смешанных дробей нужно сложить их целые части, и отдельно дробные. Если получится неправильная дробь, то из нее нужно выделить целую часть, и прибавить ее к целой части результата.

Пример. Сложим и .
Складываем целые части: 2 + 5 = 7.
Находим сумму дробных частей:
.
Поскольку 7 ≥ 6, то получили неправильную дробь. Выделяем целую часть:
.
Эту целую часть прибавляем к целой части результата. 7 + 1 = 8. Окончательно получаем:
.
Чтобы не запутаться, нужно помнить, что смешанная дробь – это сумма целой и дробной частей. Тогда процесс вычислений можно представить так:

.

Справочные данные

Основные понятия

Натуральное число

– это одно из чисел множества , используемых для счета.

Обыкновенная дробь

– это форма записи числа в виде дроби , состоящая из числителя и знаменателя , которые являются натуральными числами . Как правило, обыкновенную дробь называют просто дробью, опуская слово “обыкновенная”. Число, представленное дробью является результатом деления числителя на знаменатель . Натуральное число также можно записать в виде обыкновенной дроби, знаменатель которой равен единице: .
Дробь является рациональным числом.

Правильная дробь

– это дробь , у которой числитель меньше знаменателя:
, где .

Неправильная дробь

– это дробь, у которой числитель больше знаменателя, или равен ему.

Сокращение дроби

– это деление числителя и знаменателя дроби на их общий делитель, отличный от единицы.

Несократимая дробь

– это дробь, числитель и знаменатель которой не имеют общего делителя, кроме единицы.

Общий делитель чисел p и q

– это натуральное число , на которое делятся без остатка натуральные числа и .

Наибольший общий делитель чисел p и q

– это наибольшее натуральное число , на которое делятся без остатка натуральные числа и .
Обозначается так: N_D = НОД(p, q).

Общее кратное чисел p и q

– это натуральное число , которое делится без остатка на натуральные числа и .

Наименьшее общее кратное чисел p и q

– это наименьшее натуральное число , которое делится без остатка на натуральные числа и . Обозначается так: N_K = НОК(p, q).

Простое число

– это натуральное число, большее единицы, которое делится без остатка только на единицу и самого себя.

Разложение числа на простые множители

– это математическая операция, в результате которой исходное натуральное число представляется в виде произведения натуральных чисел, каждое из которых является простым числом.

Смешанная дробь

– это форма записи неправильной дроби, состоящая из целого числа и правильной дроби: . Смешанная дробь записывается так: . Она равна сумме целой и дробной частей:
.

Основные правила

Использованная литература:
С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. Математика. 5 класс. Москва: Просвещение, 2012.

Автор: Олег Одинцов.     Опубликовано: 12-11-2024