Типы дифференциальных уравнений
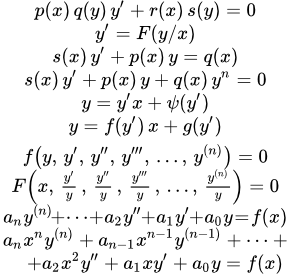
Далее в тексте s, p, q, r – функции своих аргументов. Штрих ′ означает производную по аргументу. a, b, c, a1 , b1 , c1 , a2 , b2 , c2 , ... α, β – постоянные.
Дифференциальные уравнения первого порядка
Особенности дифференциальных уравнений первого порядка
При решении уравнений первого порядка функцию y и переменную x следует считать равноправными. То есть решение может быть в виде y (x ) так и в виде x (y ) .
Дифференциальные уравнения первого порядка, разрешенные относительно производной
Уравнения с разделяющимися переменными
p (x ) q (y ) y ′ + r (x ) s (y ) = 0 ;
p (x ) q (y ) dy + r (x ) s (y ) dx = 0 . Подробнее
Приводящиеся к уравнениям с разделяющимися переменными:
y ′ = f (ax + by + c ) Подробнее
Однородные уравнения
Однородные уравнения не меняют свой вид при замене
y → ty, x → tx ,
где t – постоянная. При такой замене производная не меняется:
y ′ ≡ dydx → d (ty ) d (tx ) = tt ⋅ dydx = y ′ .
В общем виде их можно выразить через однородную функцию:
f (x, y, y ′ ) = 0 , где
f (tx, ty, y ′ ) = t p f (x, y, y ′ ) .
Уравнения, разрешенные относительно производных можно выразить через произвольную функцию:
y ′ = F ( yx ) .
Такие уравнения можно также записать посредством однородных функций:
M (x, y ) ⋅ y ′ + N (x, y ) = 0 ,
где M (x, y ) и N (x, y ) – однородные функции с равными показателями однородности p , то есть обладающие следующим свойством:
M (tx, ty ) = t p M (x, y ) , N (tx, ty ) = t p N (x, y ) . Подробнее
Приводящиеся к однородным
M (a1 x + b1 y + c1 , a2 x + b2 y + c2 ) y ′ + N (a1 x + b1 y + c1 , a2 x + b2 y + c2 ) = 0 ,
где M (u, v ) и N (u, v ) – однородные функции с равными показателями однородности. Такие уравнения можно выразить через произвольную функцию F :
y ′ = F ( a1 x + b1 y + c1 a2 x + b2 y + c2 ) . Подробнее
Обобщенно однородные уравнения не меняют свой вид при замене
y → t s y, x → tx ,
где t – постоянная, s ≠ 0, s ≠ 1 . Замена для производной:
y ′ ≡ dydx → d (t s y ) d (tx ) = t s t ⋅ dydx = t s – 1 y ′ .
В общем виде их можно записать так:
f (x, y, y ′ ) = 0 , где
f (tx, t s y, t s – 1 y ′ ) = t p f (x, y, y ′ ) .
Обобщенно однородные уравнения, разрешенные относительно производной, можно выразить через произвольную функцию:
y ′ = x s – 1 F ( yx s ) .
Их можно записать посредством однородных функций:
M (x s , y ) ⋅ xx s ⋅ y ′ + N (x s , y ) = 0 ,
где M (u, v ) и N (u, v ) – однородные функции с равными показателями однородности.
Подробнее
Линейные дифференциальные уравнения и приводящиеся к ним
- Линейное по y:
s (x ) y ′ + p (x ) y + q (x ) = 0;
s (x ) dy + (p (x ) y + q (x ) ) dx = 0. - Линейное по f(y):
s (x ) f ′(y ) y ′ + p (x ) f (y ) + q (x ) = 0;
s (x ) f ′(y ) dy + (p (x ) f (y ) + q (x ) ) dx = 0. - Линейное по x:
s (y ) x ′ + p (y ) x + q (y ) = 0;
s (y ) dx + (p (y ) x + q (y ) ) dy = 0. - Линейное по f(x):
s (y ) f ′(x ) x ′ + p (y ) f (x ) + q (y ) = 0;
s (y ) f ′(x ) dx + (p (y ) f (x ) + q (y ) ) dy = 0.
Уравнения Бернулли:
s (x ) y ′ + p (x ) y + q (x ) y n = 0 . Подробнее
Уравнения Риккати
s (x ) y ′ + p (x ) y 2 + q (x ) y + r (x ) = 0 . Подробнее
Уравнения Якоби
(a1 x + b1 y + c1 ) dx + (a2 x + b2 y + c2 ) dy + (a3 x + b3 y + c3 ) (xdy – ydx ) = 0 .
Подробнее
Уравнения в полных дифференциалах
p (x, y ) dx + q (x, y ) dy = 0 при условии ∂p∂y = ∂q∂x .
Тогда p (x, y ) dx + q (x, y ) dy = dU (x, y ) = 0 . Подробнее
Интегрирующий множитель
Если дифференциальное уравнение первого порядка не приводится ни к одному из перечисленных типов, то следует попытаться найти интегрирующий множитель, чтобы свести его к уравнению в полных дифференциалах:
p (x, y ) dx + q (x, y ) dy = 0 ;
M (x, y ) (p (x, y ) dx + q (x, y ) dy ) = M (x, y ) p (x, y ) dx + M (x, y ) q (x, y ) dy = dU = 0 . Подробнее
Уравнения, не разрешенные относительно производной y′
Уравнения, допускающие решение относительно производной y′
Сначала нужно попытаться разрешить уравнение относительно производной y′ . Если это возможно, то уравнение может быть приведено к одному из перечисленных выше типов.
Уравнения, не разрешенные относительно производной y′
Уравнения, допускающие разложение на множители:
f 1 (x, y, y ′ ) ⋅ f 2 (x, y, y ′ ) ⋅ f 3 (x, y, y ′ ) ⋅ ⋅ ⋅ f n (x, y, y ′ ) = 0 .
Подробнее
Уравнения, не содержащие x и y:
f (y ′ ) = 0 . Подробнее
Уравнения, не содержащие x или y:
f (x, y ′ ) = 0 , или f (y, y ′ ) = 0 . Подробнее
Уравнения, разрешенные относительно зависимой переменной y
Уравнения Клеро:
y = y ′x + p (y ′ ) . Подробнее
Уравнения Лагранжа:
y = f (y ′ ) x + p (y ′ ) . Подробнее
Уравнения, приводящиеся к уравнению Бернулли:
y = xy ′ + x α f (y ′ ) ;
y = xy ′ + y α f (y ′ ) . Подробнее
Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков, решаемые в квадратурах
Уравнения, содержащие переменную и старшую производную
Общий случай:
F (x, y (n ) ) = 0 . Подробнее
Разрешенные относительно старшей производной:
y (n ) = f (x ) . Подробнее
Разрешенные относительно переменной:
x = f (y (n ) ) . Подробнее
Уравнения, содержащие только производные порядков n и n-1
Общий случай:
F (y (n – 1 ) , y (n ) ) = 0 . Подробнее
Разрешенные относительно младшей производной:
y (n – 1 ) = f (y (n ) ) . Подробнее
Разрешенные относительно старшей производной:
y (n ) = f (y (n – 1 ) ) . Подробнее
Уравнения, содержащие только производные порядков n и n-2
Общий случай:
F (y (n – 2 ) , y (n ) ) = 0 . Подробнее
Разрешенные относительно старшей производной:
y (n ) = f (y (n – 2 ) ) . Подробнее
Дифференциальные уравнения, допускающие понижение порядка
Уравнения, не содержащие зависимую переменную y (и возможно несколько первых производных):
f (x, y ′, y ′′, y ′′′,..., y (n ) ) = 0 , или
f (x, y (m ) , y (m + 1 ) , y (m + 2 ) ,..., y (n ) ) = 0 . Подробнее
Уравнения, не содержащие независимую переменную x:
f (y, y ′, y ′′, y ′′′,..., y (n ) ) = 0 . Подробнее
Уравнения, однородные относительно функции и ее производных y, y′, y′′, ... :
f (x, y, y ′, y ′′,..., y (n ) ) = 0 , причем
f (x, ty, ty ′, ty ′′,..., ty (n ) ) = t p f (x, y, y ′, y ′′,..., y (n ) ) .
Их можно выразить через произвольную функцию:
F ( x, y ′y , y ′′y , y ′′′y , ⋅ ⋅ ⋅, y (n ) y ) = 0 Подробнее
Обобщенно однородные уравнения относительно переменных x, y:
f (x, y, y ′, y ′′,..., y (n ) ) = 0 , причем
f ( tx, t s y, t s dytdx , t s d 2 yt 2 dx 2 ,... , t s d n yt n dx n ) = t p f (x, y, y ′, y ′′,..., y (n ) ) .
Выраженные через произвольную функцию:
F ( yx s , y ′x s – 1 , y ′′x s – 2 , ⋅ ⋅ ⋅, y (n ) x s – n ) = 0 Подробнее
Дифференциальные уравнения с полной производной:
f (x, y, y ′, y ′′,..., y (n ) ) = ddx (Φ(x, y, y ′, y ′′,..., y (n – 1 ) ) ) = 0 . Подробнее
Линейные дифференциальные уравнения с постоянными коэффициентами и приводящиеся к ним
Линейные однородные уравнения с постоянными коэффициентами:
an y (n ) + ... + a2 y ′′ + a1 y ′ + a0 y = 0 . Подробнее
Линейные неоднородные уравнения с постоянными коэффициентами:
an y (n ) + ... + a2 y ′′ + a1 y ′ + a0 y = f (x ) .
Решение методом Бернулли (двух функций)
Решение методом Лагранжа (вариация постоянных)
Решение линейной подстановкой
Линейные неоднородные уравнения со специальной неоднородной частью:
an y (n ) + ... + a2 y ′′ + a1 y ′ + a0 y = e αx ⋅ (Ps1 (x ) cos (βx ) + Qs2 (x ) sin (βx ) ) ,
где Ps1 (x ) , Qs2 (x ) – многочлены степеней s1 и s2 . Подробнее
Уравнения Эйлера:
an x n y (n ) + an – 1 x n – 1 y (n – 1 ) + ⋅ ⋅ ⋅+ a2 x 2 y ′′+ a1 xy ′+ a0 y = f (x ) . Подробнее
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: Изменено: