Решение линейных дифференциальных уравнений с постоянными коэффициентами со специальной неоднородной частью
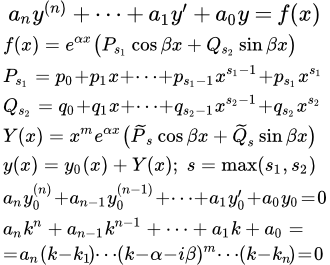
Определение общего решения по известному частному решению
Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами n-го порядка:
(1) an y (n ) + an – 1 y (n – 1 ) + an – 2 y (n – 2 ) + ⋅ ⋅ ⋅ + a1 y ′ + a0 y = f (x ) ,
где an , an – 1 , an – 2 , ... , a1 , a0 – действительные числа; f (x ) – действительная функция. Если известно частное (любое) решение Y уравнения (1), то можно найти его общее решение по формуле:
y = y0 + Y ,
где y0 – общее решение однородного уравнения:
an y (n ) 0 + an – 1 y (n – 1 ) 0 + an – 2 y (n – 2 ) 0 + ⋅ ⋅ ⋅ + a1 y ′0 + a0 y0 = 0 .
Если неоднородная часть f (x ) может быть представлена в виде суммы функций:
f (x ) = f 1 (x ) + f 2 (x ) + f 3 (x ) + ⋅ ⋅ ⋅ ,
то частное решение Y также может быть представлено в виде суммы частных решений:
Y = Y1 + Y2 + Y3 + ⋅ ⋅ ⋅ ,
каждое из которых удовлетворяет уравнению с правой частью в виде одной из функций f i (x ) :
an Y (n ) i + an – 1 Y (n – 1 ) i + ⋅ ⋅ ⋅+ a1 Y ′i + a0 Yi = f i (x ) .
Как правило, легче найти частные решения от более простых неоднородных частей, а затем получить частное решение для всего уравнения суммированием полученных частных решений.
Метод решения линейных ДУ с постоянными коэффициентами со специальной неоднородной частью
Рассмотрим линейное неоднородное уравнение со специальной неоднородной частью в виде комбинации многочленов, экспоненты, синусов и косинусов:
(2) an y (n ) + ⋅ ⋅ ⋅ + a2 y ′′ + a1 y ′ + a0 y = e αx ⋅ (Ps1 (x ) cos (βx ) + Qs2 (x ) sin (βx ) ) ,
где Ps1 (x ) , Qs2 – многочлены степеней s1 и s2 , соответственно:
Ps1 (x ) = p0 + p1 x + ⋅ ⋅ ⋅ + ps1 – 1 x s1 – 1 + ps1 x s1 ;
Qs2 (x ) = q0 + q1 x + ⋅ ⋅ ⋅ + qs2 – 1 x s2 – 1 + qs2 x s2 ;
p0 , p1 , ... , ps1 , q0 , q1 , ... , qs2 – известные коэффициенты.
Это уравнение можно решить общим методом понижения порядка. Однако существует более простой способ, основанный на том, что частное решение такого уравнения имеет определенный вид. Суть этого метода заключается в следующем.
Вначале ищем общее решение y0 однородного уравнения:
(3) an y (n ) 0 + ⋅ ⋅ ⋅ + a2 y ′′0 + a1 y ′0 + a0 y0 = 0 .
Далее устанавливаем вид частного решения Y исходного уравнения (2). Оно выражается через многочлены, экспоненту, синусы и косинусы, которые входят в частное решение с неизвестными коэффициентами. Установив вид частного решения, подставляем Y в уравнение (2). Приравнивая левую и правую части, находим неизвестные коэффициенты.
После этого общее решение исходного уравнения (2) равно сумме общего решения однородного уравнения плюс частное решение неоднородного:
y = y0 + Y .
Установление вида частного решения
Установим вид частного решения уравнения (2). Для этого вначале ищем решение однородного уравнения (3) в виде y0 = e kx . В результате, для k , получаем уравнение, которое называется характеристическим уравнением:
(4) an k n + an – 1 k n – 1 + ⋅ ⋅ ⋅+ a1 k + a0 = 0 .
Решаем это уравнение. Получаем n корней km , m = 1 ÷ n . Тогда характеристическое уравнение (4) можно представить в виде произведения множителей:
(5) an (k – k1 ) (k – k2 ) (k – k3 ) ⋅ ⋅ ⋅ (k – kn – 1 ) (k – kn ) = 0 .
Часть корней (или все) в (5) могут быть комплексными. Поэтому выразим корень km через действительную и мнимую части:
km = k ′m + ik ′′m .
Для действительного корня k ′′m = 0, km = k ′m .
Некоторые корни в (5) могут быть кратными:
km = km + 1 = ⋅ ⋅ ⋅ = km + p – 1 .
Здесь p – кратность корня. Кратный корень km кратности p входит в произведение (5) в виде множителя (k – km ) p .
Если среди корней характеристического уравнения (4) нет корня со значением
km = k ′m + ik ′′m = α + iβ ,
то частное решение уравнения (2) имеет вид:
Y = e αx ⋅ (~Ps (x ) cos (βx ) + ~Qs (x ) sin (βx ) ) ,
где s = max (s1 , s2 ) – наибольшее из s1 и s2 .
~Ps (x ) = A0 + A1 x + A2 x 2 + ⋅ ⋅ ⋅ + As x s ,
~Qs (x ) = B0 + B1 x + B2 x 2 + ⋅ ⋅ ⋅ + Bs x s
– многочлены степени s с неизвестными коэффициентами Am , Bm , которые подлежат определению подстановкой в уравнение (2).
Если среди корней характеристического уравнения (4) есть корень кратности p со значением
km = k ′m + ik ′′m = α + iβ
то частное решение уравнения (2) имеет вид:
Y = x p ⋅ e αx ⋅ (~Ps (x ) cos (βx ) + ~Qs (x ) sin (βx ) ) ,
где также s = max (s1 , s2 ) – наибольшее из s1 и s2 .
~Ps (x ) = A0 + A1 x + A2 x 2 + ⋅ ⋅ ⋅ + As x s ,
~Qs (x ) = B0 + B1 x + B2 x 2 + ⋅ ⋅ ⋅ + Bs x s
– многочлены степени s с неизвестными коэффициентами Am , Bm .
Когда вид частного решения установлен, подставляем Y в уравнение (2) и находим неизвестные коэффициенты A0 , A1 , A2 , ..., As , B0 , B1 , B2 , ..., Bs , приравнивая левую и правую части уравнения. После чего получаем общее решение уравнения (2):
y = y0 + Y .
Далее рассмотрен пример решения неоднородного дифференциального уравнения со специальной неоднородной частью.
Частные случаи
Неоднородность в виде многочлена
Теперь рассмотрим некоторые более простые виды специальной неоднородности. Начнем с неоднородной части в виде многочлена:
an y (n ) + ⋅ ⋅ ⋅ + an – 2 y ′′ + a1 y ′ + a0 y = Ps (x ) ,
где Ps (x ) = p0 + p1 x + ⋅ ⋅ ⋅ + ps – 1 x s – 1 + ps x s – многочлен степени s . Этот случай принадлежит к общему виду специальной неоднородности (2), в котором α = 0, β = 0 . Основываясь на вышеизложенном, получаем следующие правила составления вида частного решения.
Если среди корней km характеристического уравнения (4) нет нулевого корня
km ≠ 0, m = 1 ÷ n ,
то частное решение имеет вид:
Y = ~Ps (x ) = A0 + A1 x + ⋅ ⋅ ⋅ + As – 1 x s – 1 + As x s .
То есть оно является многочленом степени s с неопределенными коэффициентами Am .
Если характеристическое уравнение (4) имеет нулевой корень кратности p :
km = km + 1 = ⋅ ⋅ ⋅ = km + p – 1 = 0 ,
то частное решение имеет вид:
Y = x p ⋅ ~Ps (x ) = x p (A0 + A1 x + ⋅ ⋅ ⋅ + As – 1 x s – 1 + As x s ) .
Неоднородность в виде произведения экспоненты и многочлена
Теперь рассмотрим неоднородную часть в виде произведения многочлена степени s и экспоненты:
an y (n ) + ⋅ ⋅ ⋅ + an – 2 y ′′ + a1 y ′ + a0 y = Ps (x ) e αx .
Этот случай принадлежит к общему виду (2), в котором β = 0 .
Если среди корней km характеристического уравнения нет действительного корня со значением α :
km ≠ α, m = 1 ÷ n ,
то частное решение является произведением многочлена степени s и экспоненты:
Y = ~Ps (x ) e αx = (A0 + A1 x + ⋅ ⋅ ⋅ + As – 1 x s – 1 + As x s ) e αx .
Если характеристическое уравнение (4) имеет действительный корень α кратности p :
km = km + 1 = ⋅ ⋅ ⋅ = km + p – 1 = α ,
то частное решение имеет вид:
Y = x m ⋅ ~Ps (x ) ⋅ e αx = x p (A0 + A1 x + ⋅ ⋅ ⋅ + As – 1 x s – 1 + As x s ) e αx .
Неоднородность в виде суммы произведений многочленов на косинус и синус
Наконец рассмотрим неоднородную часть в виде суммы произведений многочленов степеней s1 , s2 на косинус и синус:
an y (n ) + ⋅ ⋅ ⋅ + an – 2 y ′′ + a1 y ′ + a0 y = Ps1 (x ) cos (βx ) + Qs2 (x ) sin (βx ) .
Этот случай принадлежит к общему виду (2), в котором α = 0 .
Если среди корней km характеристического уравнения нет чисто мнимого корня со значением iβ :
km ≠ iβ, m = 1 ÷ n ,
то частное решение является суммой произведений многочленов, косинуса и синуса:
Y = ~Ps (x ) cos (βx ) + ~Qs (x ) sin (βx ) ,
где s = max (s1 , s2 ) – наибольшее из s1 и s2 .
~Ps (x ) = A0 + A1 x + A2 x 2 + ⋅ ⋅ ⋅ + As x s ,
~Qs (x ) = B0 + B1 x + B2 x 2 + ⋅ ⋅ ⋅ + Bs x s
– многочлены степени s с неизвестными коэффициентами Am , Bm .
Если характеристическое уравнение (4) имеет чисто мнимый корень iβ кратности p :
km = km + 1 = ⋅ ⋅ ⋅ = km + p – 1 = iβ ,
то частное решение имеет вид:
Y = x p ⋅ (~Ps (x ) cos (βx ) + ~Qs (x ) sin (βx ) ) .
То есть частное решение как и в предыдущем случае, но умноженное на x p .
Автор: Олег Одинцов. Опубликовано: Изменено: