Решение линейных неоднородных дифференциальных уравнений высших порядков методом Лагранжа
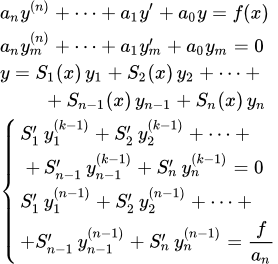
Метод Лагранжа (вариация постоянных)
Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами произвольного n-го порядка:
(1) .
Метод вариации постоянной, рассмотренный нами для уравнения первого порядка, также применим и для уравнений более высоких порядков.
Решение выполняется в два этапа. На первом этапе мы отбрасываем правую часть и решаем однородное уравнение. В результате получаем решение, содержащее n произвольных постоянных. На втором этапе мы варьируем постоянные. То есть мы считаем, что эти постоянные являются функциями от независимой переменной x и находим вид этих функций.
Хотя мы здесь рассматриваем уравнения с постоянными коэффициентами, но метод Лагранжа также применим и для решения любых линейных неоднородных уравнений. Для этого, однако, должна быть известна фундаментальная система решений однородного уравнения.
Шаг 1. Решение однородного уравнения
Как и в случае уравнений первого порядка, вначале мы ищем общее решение однородного уравнения, приравнивая правую неоднородную часть к нулю:
(2) .
Общее решение такого уравнения имеет вид:
(3) .
Здесь – произвольные постоянные; – n линейно независимых решений однородного уравнения (2), которые образуют фундаментальную систему решений этого уравнения.
Шаг 2. Вариация постоянных – замена постоянных функциями
На втором этапе мы займемся вариацией постоянных. Другими словами, мы заменим постоянные на функции от независимой переменной x:
.
То есть мы ищем решение исходного уравнения (1) в следующем виде:
(4) .
Если мы подставим (4) в (1), то получим одно дифференциальное уравнение для n функций . При этом мы можем связать эти функции дополнительными уравнениями. Тогда получится n уравнений, из которых можно определить n функций . Дополнительные уравнения можно составить различными способами. Но мы это сделаем так, чтобы решение имело наиболее простой вид. Для этого, при дифференцировании, нужно приравнивать к нулю члены, содержащие производные от функций . Продемонстрируем это.
Чтобы подставить предполагаемое решение (4) в исходное уравнение (1), нам нужно найти производные первых n порядков от функции, записанной в виде (4). Дифференцируем (4), применяя правила дифференцирования суммы и произведения:
.
Сгруппируем члены. Сначала выпишем члены с производными от , а затем – члены с производными от :
.
Наложим на функции первое условие:
(5.1) .
Тогда выражение для первой производной по будет иметь более простой вид:
(6.1) .
Тем же способом находим вторую производную:
.
Наложим на функции второе условие:
(5.2) .
Тогда
(6.2) .
И так далее. В дополнительных условиях, мы приравниваем члены, содержащие производные функций , к нулю.
Таким образом, если выбрать следующие дополнительные уравнения для функций :
(5.k) ,
то первые производных по будут иметь наиболее простой вид:
(6.k) .
Здесь .
Находим n-ю производную:
(6.n)
.
Подставляем в исходное уравнение (1):
(1) ;
.
Учтем, что все функции удовлетворяют уравнению (2):
.
Тогда сумма членов, содержащих дают нуль. В итоге получаем:
(7) .
В результате мы получили систему линейных уравнений для производных :
(5.1) ;
(5.2) ;
(5.3) ;
. . . . . . .
(5.n-1) ;
(7′) .
Решая эту систему, находим выражения для производных как функции от x. Интегрируя, получим:
.
Здесь – уже не зависящие от x постоянные. Подставляя в (4), получаем общее решение исходного уравнения.
Заметим, что для определения величин производных мы нигде не использовали тот факт, что коэффициенты ai являются постоянными. Поэтому метод Лагранжа применим для решения любых линейных неоднородных уравнений, если известна фундаментальная система решений однородного уравнения (2).
Далее рассмотрены примеры решения уравнений методом Лагранжа.
Примеры
Решить уравнения методом вариации постоянных (Лагранжа).
Решение примеров > > >
Автор: Олег Одинцов. Опубликовано: Изменено:
