Определение и свойства момента силы

Определения и свойства момента силы относительно точки и оси. Определение плеча силы. Выражение абсолютного значения момента в виде произведения плеча на модуль силы.

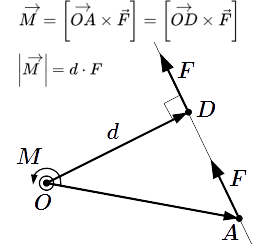
Момент силы относительно точки

Определение момента

Момент силы относительно точки

Пусть сила приложена в точке A с радиус вектором ; O – произвольная точка с радиус вектором .
Моментом этой силы относительно точки O называется векторное произведение на вектор силы :
(1)   .
Здесь – вектор, проведенный из точки O в точку A.

Момент силы имеет несколько вариантов записи:
.
Во втором случае – это условное обозначение совокупности двух векторов – вектора силы и вектора точки ее приложения .

Если выбрать прямоугольную систему координат Oxyz с центром в точке O, то ,   . Момент силы будет иметь следующие компоненты:
(1.1)   ;
(1.2)   ;
(1.3)   .
Здесь – координаты точки A в выбранной системе координат. Компоненты представляют собой значения момента силы относительно осей , соответственно.

Определение плеча силы

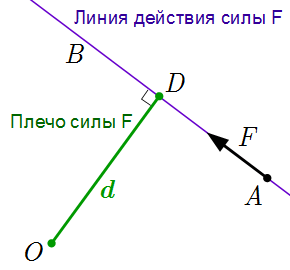
Плечо силы относительно точки

– это расстояние между линией действия силы и точкой, относительно которой определяется плечо. То есть плечо силы – это длина перпендикуляра, опущенного из точки на линию действия силы.

На рисунке d = |OD| – плечо силы F, приложенной в точке A; OD ⊥ AB; AB – линия действия силы.

Свойства

Тоже самое относится и к силам, чьи линии продолжения пересекаются в одной точке. При этом в качестве точки приложения суммы сил берется точка пересечения линий их действия.

Это свойство следует из свойства векторного произведения. Поскольку векторы и являются истинными (или полярными) векторами, то их векторное произведение является псевдовектором. Это означает то, что мы можем определить только абсолютное значение и ось, вдоль которой направлено векторное произведение. Само же направление по этой оси мы задаем произвольным образом, используя правило правого винта. То есть мы, мысленно откладываем векторы и из одного центра. Затем поворачиваем ручку из положения в положение . В результате правый винт смещается в направлении, перпендикулярном плоскости, в которой расположены векторы. Это направление мы и берем за направление векторного произведения.

Но если бы мы определили направление по правилу левого винта, то векторное произведение было бы направлено в противоположную сторону. При этом никакого противоречия не возникает. То есть фактически, аксиальные векторы могут иметь два взаимно противоположных направления. Чтобы не усложнять математические формулы, мы выбираем одно из них. По этой причине, псевдовекторы нельзя геометрически складывать с истинными векторами. Но их можно перемножать, используя скалярное или векторное произведение.

Момент силы относительно оси

Определение

Часто встречаются случаи, когда нам не нужно знать все компоненты, а нужно знать только момент силы относительно выбранной оси.

Момент силы относительно оси

– это проекция вектора момента силы относительно произвольной точки, принадлежащей этой оси, на направление оси.

Пусть – единичный вектор, направленный вдоль оси. И пусть O – произвольная точка, принадлежащая ей. Тогда момент силы относительно оси является скалярным произведением:
.
Такое определение возможно, поскольку для любых двух точек O и O′, принадлежащих оси, проекции моментов относительно этих точек на ось равны. Покажем это.

Воспользуемся векторным уравнением :

;
.
Умножим это уравнение скалярно на единичный вектор , направленный вдоль оси:
.
Поскольку вектор параллелен оси, то . Отсюда
.
То есть проекции моментов на ось, относительно точек O и O′, принадлежащих этой оси, равны.

Свойства

Доказательство свойств

Доказательство

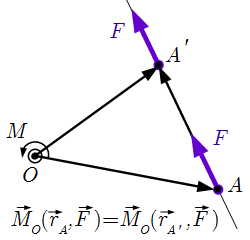
Пусть сила приложена в точке A. Проведем через нее прямую, параллельную вектору . Эта прямая называется линией действия силы. Переместим точку приложения силы в точку A′, принадлежащую линии действия. Пусть O – произвольная точка. Тогда
(2.1)   ,
где вектор параллелен . Воспользуемся тем, что векторное произведение параллельных векторов равно нулю:
(2.2)   .

Найдем момент силы, приложенной в точке A′, применяя (2.1) и (2.2):

.
Мы видим, что момент не изменился:
.

Свойство доказано.

Доказательство

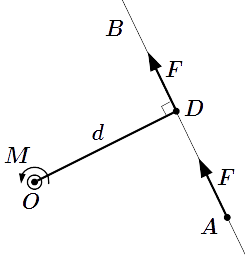
Пусть мы имеем силу , приложенную в точке A. Рассмотрим момент этой силы относительно некоторой точки O. Заметим, что точки O, A и вектор лежат в одной плоскости. Изобразим их на рисунке. Через точку A, параллельно вектору , проводим прямую AB – линию действия силы. Из точки O опустим перпендикуляр OD к AB. Пусть D – точка пересечения линии действия и перпендикуляра. Тогда – плечо силы относительно центра O. Обозначим его буквой . Воспользуемся предыдущим свойством ⇑, согласно которому момент не изменится, если точку приложения силы переместить вдоль ее линии действия. Переместим ее в точку D. Момент силы:
.
Поскольку векторы и перпендикулярны, то по свойству векторного произведения, абсолютное значение момента:
,
где – абсолютное значение силы.

Свойство доказано.

Заметим, что вектор момента перпендикулярен плоскости рисунка. Его направление определяется по правилу правого винта. Если мы будем вращать винт, проходящий через точку O перпендикулярно плоскости рисунка, в направлении силы F, то он будет перемещаться на нас. Поэтому вектор момента перпендикулярен плоскости рисунка и направлен на нас.

Автор: Олег Одинцов.     Опубликовано: 20-09-2019   Изменено: 27-02-2024