Определение реакций опор балки – решение задачи
Как определить реакции опор балки
- Выбираем систему координат. Можно ось x направить вдоль балки, ось y – вертикально вверх. Ось z будет направлена перпендикулярно плоскости рисунка, на нас. Центр системы координат можно выбрать в одной из точек опор балки.
- Отбрасываем опоры и заменяем их силами реакций.
- Если есть распределенная нагрузка, то заменяем ее равнодействующей силой. Величина этой силы равна площади эпюры нагрузки. Точка приложения силы находится в центре тяжести эпюры. Так если нагрузка q равномерно распределена на отрезке AD, то ее равнодействующая имеет величину Q = q·|AD| и приложена посередине отрезка AD (точка C).
- Составляем уравнения равновесия для действующих сил. В общем случае они имеют вид:
.
Спроектируем это векторное уравнение на оси координат. Тогда сумма проекций сил на каждую из осей координат равна нулю:
(1) .
Находим проекции сил на оси координат и составляем уравнения (1). Для плоской системы сил, последнее уравнение с проекциями на ось z, не используется. - Составляем уравнения равновесия для моментов сил. Сумма моментов сил относительно произвольной оси A′A′′ равна нулю:
(2) .
Чтобы составить это уравнение, мы должны выбрать одну или несколько осей, относительно которых вычисляются моменты. Как правило, вычисления будут более простыми, если оси проходят через точки опор балки, перпендикулярно плоскости рисунка. - Для плоской задачи достаточно составить одно уравнение (2) для одной оси. Если балка имеет две опоры, то можно составить два уравнения (2) для двух осей, проходящих через опоры перпендикулярно плоскости рисунка (см. Второй способ решения ⇓).
- Для пространственного распределения сил, нужно составить минимум три уравнения (2) для трех осей.
- Решаем уравнения и получаем значения реакций опор.
- Если число переменных в полученной системе больше числа линейно независимых уравнений, то задача статически неопределима. Она имеет бесконечно много решений. Выбрать единственное решение методами статики нельзя. Это можно сделать методами сопротивления материалов.
- Делаем проверку результата. В качестве проверки можно выбрать любую новую ось, и относительно нее подсчитать сумму моментов сил, действующих на балку, включая найденные реакции опор. Сумма моментов должна равняться нулю.
Пример решения задачи на определение реакций опор балки

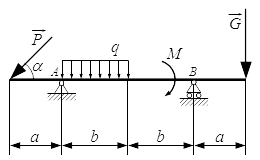
Жесткая балка, линейные размеры которой указаны на рисунке 1, закреплена в точках А и В. На балку действуют пара сил с моментом М, равномерно распределенная нагрузка интенсивностью q и две силы P и G, место приложения которых показано на рисунке.
Определить реакции опор балки в точках A и B, вызываемые указанными нагрузками.
Дано:
P = 20,2 Н; G = 22,6 Н; q = 2 Н/м; M = 42,8 Н·м; a = 1,3 м; b = 3,9 м; α = 45°;
Решение задачи
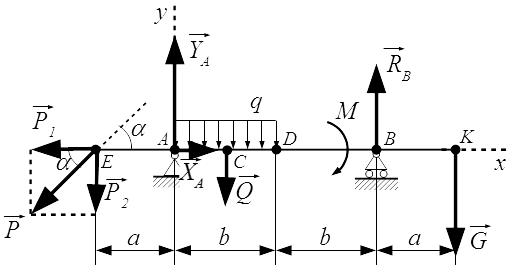
Проводим оси x и y системы координат. Начало системы координат поместим в точку A. Ось x направим горизонтально, вдоль балки. Ось y – вертикально. Ось z перпендикулярна плоскости рисунка и направлена на нас. На рисунке она не указана.

Отбрасываем опоры и заменяем их силами реакций.
В шарнире A, разложим силу реакции на составляющие и вдоль осей координат.
Реакция , в подвижной опоре на катках, направлена вертикально. Предполагаемые направления реакций опор выбираем по своему усмотрению, наугад. Если ошибемся с направлением реакции, то получим отрицательное значение, что будет говорить о том, что соответствующая сила реакции направлена в противоположную сторону.
Заменим равномерно распределенную нагрузку q равнодействующей . Абсолютное значение равнодействующей равно площади эпюры:
Н.
Точка приложения равнодействующей находится в центре тяжести эпюры. Поскольку эпюра представляет собой прямоугольник, то ее центр тяжести находится в точке C – посередине отрезка AD:
AC = CD = b/2 = 1,95 м.
Уравнения равновесия для сил
Определяем проекции сил на оси координат.
Разложим силу на составляющие вдоль координатных осей:
.
Абсолютные значения составляющих:
.
Вектор параллелен оси x и направлен в противоположную от нее сторону. Вектор параллелен оси y и также направлен в противоположную сторону. Поэтому проекции силы на оси координат имеют следующие значения:
.
Остальные силы параллельны осям координат. Поэтому они имеют следующие проекции:
;
;
;
;
.
Составляем уравнения равновесия для сил.
Сумма проекций всех сил на ось x равна нулю:
;
;
;
(П1) .
Сумма проекций всех сил на ось y равна нулю:
;
;
;
(П2) .
Уравнения равновесия для моментов
Итак, мы уже составили два уравнения для сил: (П1) и (П2). Но в них есть три неизвестные величины: , и . Чтобы их определить, нам нужно составить еще одно уравнение.
Составим уравнение равновесия для моментов сил. Для этого нам нужно выбрать ось, относительно которой мы будем вычислять моменты. В качестве такой оси возьмем ось, проходящую через точку A, перпендикулярно плоскости рисунка. За положительное направление выберем то, которое направлено на нас. Тогда, по правилу правого винта, положительным направлением закручивания будет направление против часовой стрелки.
Находим моменты сил относительно выбранной оси.
Силы , и пересекают ось. Поэтому их моменты равны нулю:
; ; .
Сила перпендикулярна плечу AB. Ее момент:
.
Поскольку, относительно оси A, сила направлена против часовой стрелки, то ее момент положительный.
Сила перпендикулярна плечу AK. Поскольку, относительно оси A, эта сила направлена по часовой стрелки, то ее момент имеет отрицательное значение:
.
Аналогичным способом находим моменты остальных сил:
;
.
Момент от пары сил M не зависит от точек приложения сил, входящих в пару:
.
Составляем уравнение равновесия. Сумма моментов сил относительно оси A равна нулю:
;
;
;
(П3) .
Решение уравнений равновесия
Итак, для трех неизвестных величин, мы получили три уравнения:
(П1) .
(П2) .
(П3) .
Решаем эти уравнения. Вычисляем расстояния.
м;
м;
м;
м.
Из уравнения (П1) находим:
Н.
Из уравнения (П3) находим:
Н.
Из уравнения (П2) имеем:
Н.
Абсолютное значение реакции опоры в точке A:
Н.
Проверка правильности решения
Чтобы проверить, правильно ли мы определили реакции опор балки, найдем сумму моментов сил относительно другой оси. Если мы нашли реакции правильно, то она должна равняться нулю.
Возьмем ось, проходящую через точку E. Вычисляем сумму моментов сил относительно этой оси:
.
Найдем погрешность вычисления суммы моментов. Найденные силы мы округлили до двух знаков после запятой. То есть погрешность определения реакций опор составляет 0,01 Н. Расстояния, по порядку величины, примерно равны 10 м. Тогда погрешность вычисления суммы моментов составляет около 10·0,01 = 0,1 Нм. Мы получили значение -0,03 Нм. Эта величина отличается от нуля не более, чем на величину погрешности. То есть, с учетом погрешности вычислений, сумма моментов относительно другой оси равна нулю. Значит решение правильное, силы реакций найдены верно.
Ответ
Н; Н; Н; Н.
Второй способ решения
Первым способом мы составили два уравнения для сил и одно – для моментов. Задачу можно решить другим способом, составив два уравнения для моментов и одно для сил.
Воспользуемся тем, что сумма моментов сил равна нулю относительно любой оси. Возьмем вторую ось, которая проходит через точку B перпендикулярно плоскости рисунка. Сумма моментов сил относительно этой равна нулю:
.
Вычисляем моменты сил относительно оси B.
; ; ;
;
;
;
;
.
Сумма моментов сил относительно оси B равна нулю:
;
;
;
(П4) ;
Итак, вторым способом, мы также имеем три уравнения:
(П1) .
(П3) ;
(П4) .
Здесь каждое уравнение содержит только одну неизвестную величину. Реакции и определяются из тех же уравнений, что и ранее. Находим силу из уравнения (П4):
Н.
Значение реакции совпало со значением, полученным первым способом из уравнения (П2).
Автор: Олег Одинцов. Опубликовано: Изменено:
