Центр системы параллельных сил

Определение центра параллельных сил. Доказано двумя способами, что система сил, параллельных некоторой оси, векторная сумма которых не равна нулю, имеет равнодействующую, проходящую через центр параллельных сил.

Содержание

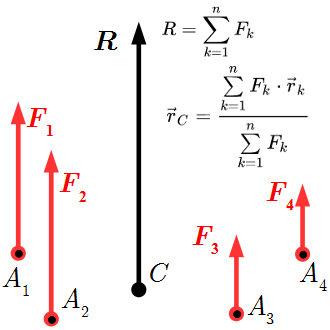
Теорема о центре параллельных сил

Пусть имеется система параллельных сонаправленных сил

, каждая из которых приложена к твердому телу в точке A_k с радиус-вектором

.
Тогда эта система сил имеет равнодействующую

, сонаправленную силам, модуль которой равен сумме их модулей
(1.1)

,
и приложенную к центру параллельных сил, радиус-вектор которого определяется по формуле:
(1.2)

.
Доказательство, используя уравнения статики
Доказательство методом математической индукции

Эта теорема широко применяется в распространенном случае, когда на материальные точки, составляющие тело, действуют силы тяжести вблизи поверхности земли, которые можно считать параллельными и сонаправленными. Теорема позволяет заменить их одной равнодействующей, приложенной к центру параллельных сил, который в этом случае называется центром тяжести тела.

Заметим, что положение центра параллельных сил зависит от модулей сил, но не от их направления. По этой причине центр тяжести связан с телом, и является его геометрической характеристикой.

Эту теорему можно обобщить и на случай, когда имеются и противоположно направленные силы. Тогда равнодействующая существует, если геометрическая сумма сил не равна нулю:
(1.3) .
Ее вектор равен сумме векторов сил:
(1.4) ;
модуль равен сумме проекций сил на направление равнодействующей :
(1.5) .
Если сила сонаправлена равнодействующей, то . Если направлена противоположно, то .
Равнодействующая приложена к центру параллельных сил, радиус-вектор которого определяется по формуле:
(1.6) .
Формулы остаются такими, как и для случая сонаправленных сил, только модули сил, направленных противоположно равнодействующей, входят со знаком минус.
Доказательство, используя уравнения статики
Доказательство методом математической индукции

Добавим, что если геометрическая сумма сил равна нулю, а сумма моментов сил относительно произвольной точки отлична от нуля, то эта система эквивалентна паре сил. Если же и сумма моментов сил относительно произвольной точки равна нулю, то это система взаимно уравновешивающихся сил.

Центр параллельных сил: – это точка C, через которую проходит равнодействующая параллельных сил при любом направлении этих сил. Ее радиус вектор определяется по формуле:
,
где – точка приложения силы , – ее модуль. Здесь подразумевается, что все силы параллельны и сонаправлены.
Если имеются противоположно направленные силы, то
,
где , если сила направлена вдоль равнодействующей ,
и , если сила направлена противоположно . То есть – это проекция силы на направление равнодействующей.

Доказательство теоремы, используя уравнения статики

Согласно определению, равнодействующая – это одна сила, действие которой на твердое тело эквивалентно действию заданной системы сил. То есть при замене системы сил на равнодействующую, законы движения твердого тела (или законы статики) должны быть неизменными. В законы движения твердого тела входит только векторная сумма сил и векторная сумма моментов сил относительно произвольного центра (главный вектор и главный момент). Поэтому при замене системы сил на равнодействующую значения главного вектора и главного момента должны оставаться неизменными.

Математически это означает, что при замене системы n сил , каждая из которых приложена в точке с радиус-вектором на одну равнодействующую силу , приложенную в точке C с радиус-вектором , должны выполняться следующие векторные уравнения:
(2.1) ;
(2.2) .
Подразумевается, что начало системы отсчета выбрано в некоторой точке O.

Такая замена возможно не всегда. Например, пару двух равных по модулю, но противоположных по направлению сил нельзя заменить одной равнодействующей. Покажем, что систему параллельных сонаправленных сил, можно заменить равнодействующей, приложенной к центру параллельных сил (1.2).

Введем единичный вектор , направленный вдоль сил . Поскольку они параллельны и сонаправлены, то
(2.3) ,
где – модуль силы. Подставим в (2.1):
,
где .
Тем самым мы нашли, что равнодействующая. если она существует, направлена вдоль вектора , то есть сонаправлена приложенным силам, и ее модуль определяется по формуле (1.1).

Теперь покажем, что равнодействующая существует: то есть можно найти такой вектор , при котором выполняется (2.2). Подставим (2.3) в (2.2), и выполним преобразования.

.
Мы получили, что (2.2) выполняется, если положить
(2.4) .

Мы нашли вектор , но это не значит, что он определяет точку в пространстве. Для этого нам нужно по казать, что является радиус-вектором, то есть при параллельном переносе системы координат, начало которой перемещается из точки O в точку O′, его компоненты преобразуются как компоненты любого радиус-вектора, по закону:
(2.5) ,
где – радиус-вектор точки в новой системе координат с началом в O′. См. страницу «Что такое радиус-вектор, и чем он отличается от других векторов». Подставим (2.5) в (2.4):

;
.
Тем самым мы нашли, что, при параллельном переносе системы координат, компоненты вектора преобразуются по закону (2.5). То есть является радиус-вектором, и поэтому определяет положение точки в пространстве, связанную с твердым телом.

Теорема доказана.

Случай противоположно направленных сил

Если имеются противоположно направленные силы, то вышеизложенный вывод сохраняет силу, если в нем заменить модули сил их проекциями на направление равнодействующей:
.
В результате получаем (1.5) и (1.6):
;
.
При получаем деление на нуль. Поэтому параллельные противоположно направленные силы имеют равнодействующую только при .

Доказательство методом математической индукции

На странице «Система двух параллельных сил» мы нашли равнодействующую для системы, состоящей из двух параллельных сил. Если нам нужно найти равнодействующую трех параллельных сил , то можно поэтапно применять этот результат. То есть в начале две силы и заменим их равнодействующей . В результате получим эквивалентную систему, но состоящую уже из двух сил: и . Эту систему также можно заменить равнодействующей , которая и будет эквивалентна действию исходных трех сил.

Далее этот результат можно обобщить на случай произвольного количества сил, применяя метод математической индукции.

Сначала рассмотрим случай параллельных сонаправленных сил. А затем, отталкиваясь от него, докажем теорему, когда могут присутствовать силы в противоположном направлении.

Доказательство для параллельных сонаправленных сил

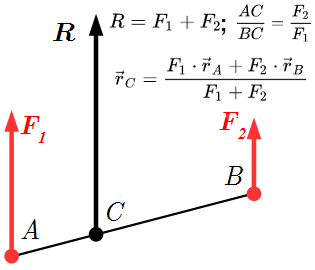
Равнодействующая двух сонаправленных параллельных сил — Две сонаправленные параллельные силы F₁ и F₂ имеют равнодействующую R.

На странице «Равнодействующая системы двух параллельных сил» мы показали, что две сонаправленные параллельные силы и , приложенные в точках A и B с радиус-векторами и , имеют равнодействующую , которая сонаправлена силам . По модулю она равна
(3.1) ,
и приложена к точке C с радиус вектором
(3.2) .

Теперь рассмотрим систему, состоящую из трех сонаправленных параллельных сил , приложенных в точках A₁, A₂, A₃ с радиус-векторами .

По формулам (3.1) и (3.2) найдем равнодействующую и точку ее приложения первых двух сил:
;
.

Мы получили систему, эквивалентную исходной, состоящую из двух сил и , приложенных в точках с радиус-векторами и . Снова, по тем же формулам, находим их равнодействующую и точку ее приложения , которые уже будут являться равнодействующей исходной системы сил:
;
;
.

Это наводит на мысль, что в общем случае n сил, равнодействующая имеет модуль
,
и приложена к точке
.
Докажем это методом математической индукции.

Для теорема доказана (см. «Равнодействующая системы двух параллельных сил»).

Предположим, что теорема верна для . То есть система, состоящая из параллельных сонаправленных сил имеет равнодействующую с модулем
(3.3) ,
приложенную в точке C_m с радиус вектором
(3.4) .
Нам нужно доказать, что система из m+1 сил имеет равнодействующую
(3.5) ,
приложенную в точке
(3.6) .

Рассмотрим систему, состоящую из m+1 параллельных сонаправленных сил . Воспользуемся предположением, и заменим силы равнодействующей (3.3), приложенной в точке C_m с радиус-вектором (3.4). Тогда мы получим систему, состоящую из двух параллельных сонаправленных сил и . Применим теорему, доказанную для двух сил. Эта система имеет равнодействующую
(3.7) ,
приложенную в точке
(3.8) .

Подставим (3.3) в (3.7).
.
Получили (3.5).

Подставим (3.4) в (3.8).
;
;
.
Получили (3.6).

Для случая сонаправленных параллельных сил, теорема доказана.

Доказательство для противоположно направленных сил

Теперь рассмотрим случай, когда имеются противоположно направленные силы. Пронумеруем их так, чтобы первые m сил были направлены в одну сторону, а последние – в противоположную. И пусть
.
Введем единичный вектор , сонаправленный первой группе сил.

Согласно доказанному выше, первые m сил имеют равнодействующую
;
(4.1) .
Она приложена в точке с радиус-вектором
(4.2) .
Последние сил также сонаправлены и имеют равнодействующую
;
(4.3) .
Она противоположно направлена , и приложена в точке с радиус вектором
(4.4) .

Заменим первые m сил равнодействующей , приложенной в точке ; а последние – равнодействующей , приложенной в точке . Получим эквивалентную систему, состоящую из двух, противоположно направленных, не равных по модулю, сил.

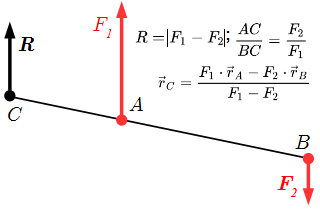
Равнодействующая двух противоположно направленных параллельных сил — Две не равные противоположно направленные силы F₁ и F₂ имеют равнодействующую R.

Ранее мы нашли, что система двух не равных по модулю, противоположно направленных параллельных сил имеет равнодействующую. В нашем случае, модуль и точка приложения равнодействующей определяются по формулам:
(4.5) ;
(4.6) .

Подставляя (4.1) и (4.3) в (4.5), получим (1.5):
,
где , если сила сонаправлена с , и , если противоположна .

Найдем точку приложения равнодействующей . Для этого подставляем (4.2) и (4.4) в (4.6), и выполняем преобразования:
;
.

Обобщенная теорема доказана.

Автор: Олег Одинцов. Опубликовано: 25-03-2024 Изменено: 09-10-2024