Равнодействующая системы двух параллельных сил

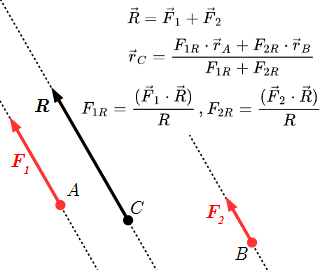
Расчет равнодействующей системы двух параллельных сил тремя способами, используя аксиомы статики и уравнения равновесия.

Точку приложения равнодействующей, как и сил и , можно перемещать вдоль их линий действия. Поэтому в качестве точки приложения равнодействующей можно выбрать любую точку C′ с радиус вектором
,
где – произвольная постоянная.

Параллельные силы и могут быть сонаправлены или направлены в противоположные стороны. Приведем формулы для каждого из этих случаев по отдельности.

Равнодействующая двух сонаправленных параллельных сил

Две однонаправленные параллельные силы и , приложенные к твердому телу в точках A и B,
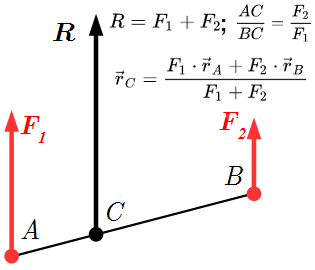
имеют равнодействующую , сонаправленную параллельно и . Абсолютная величина равнодействующей равна сумме абсолютных величин сил:
(1.1)   .
Она приложена в точке C, на отрезке AB, и делит его обратно пропорционально модулям сил:
(1.2)  
(1.3)   .
Радиус вектор точки приложения C определяется по формуле
(1.4)   ,
где – радиус векторы точек A и B.
Доказательство

Равнодействующая двух противоположно направленных параллельных сил

Две не равные по модулю противоположно направленные силы и , приложенные к твердому телу в точках A и B,
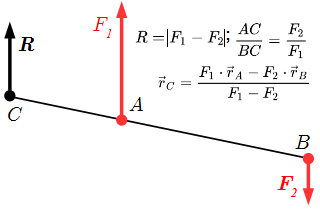
имеют равнодействующую , направление которой совпадает с направлением наибольшей по абсолютной величине силы или . Абсолютная величина равнодействующей равна модулю разности абсолютных величин сил:
(2.1)   .
Она приложена в точке C, на продолжении отрезка AB, причем:
(2.2)  
(2.3)   .
Радиус вектор точки приложения C определяется по формуле
(2.4)   ,
где – радиус векторы точек A и B.
Доказательство

Две равные по абсолютной величине и противоположно направленные силы, линии действия которых не совпадают, не имеют равнодействующей. Такая система называется парой сил и характеризуется моментом.

Вывод формул

Используя аксиомы статики

Вначале найдем равнодействующую, используя аксиомы статики. Суть аксиом заключается в том, что силы, приложенные к твердому телу, являются скользящими векторами. То есть силы, приложенные к одной точке можно складывать по правилу параллелограмма, и точку приложения силы можно перемещать вдоль ее линии действия.

Мы сразу можем упростить задачу, если переместим точки приложения A и B сил так, чтобы прямая, проходящая через точки приложения была перпендикулярна направлению сил: . После того как мы найдем точку приложения C равнодействующей , мы также можем переместить ее вдоль линии действия равнодействующей. В результате все формулы, полученные для случая , будут применимы и для произвольно расположенных точек A и B.

Две силы одного направления

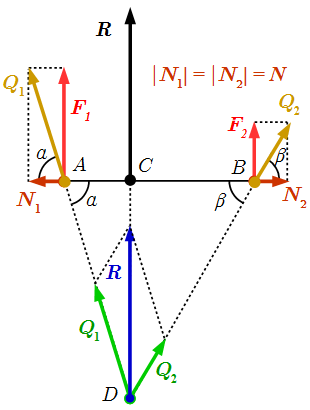
1. Переместим точки приложения параллельных сил и вдоль их линий действия в точки A и B так, чтобы .
2. Добавим систему взаимно уравновешивающихся сил и , приложенных к точкам A и B. Они равны по абсолютной величине, противоположны по направлению, и их линии действия совпадают с прямой AB. В результате получим эквивалентную систему сил, состоящую из , приложенных к A, и , приложенных к B.
3. Сложим силы и по правилу параллелограмма: . Тоже самое проделаем с и : . В результате получим эквивалентную систему сил, состоящую из и , приложенных к точкам A и B, соответственно. Эти силы составляют углы и с прямой AB, причем:
(3.1)   ,
где – абсолютная величина сил и .
4. Найдем точку D пересечения линий действия сил и , и перенесем точки приложения этих сил в D. В результате получим эквивалентную систему сил, состоящую из и , приложенных к точке D.
5. Сложим и по правилу параллелограмма. В результате получим эквивалентную систему сил, состоящую из одной равнодействующей силы . Легко показать, что :
.
Поскольку силы и перпендикулярны AB, то равнодействующая также перпендикулярна AB.
6. Наконец, перенесем точку приложения равнодействующей вдоль ее линии действия в точку C, чтобы точки A, B и C располагались на одной прямой. Применяя (3.1), из прямоугольников ACD и BCD находим:
;
;
;

;
;

.

Две противоположно направленные силы

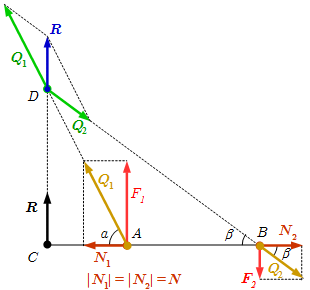
1. Переместим точки приложения сил и вдоль их линий действия в точки A и B так, чтобы .
2. Добавим систему взаимно уравновешивающихся сил и , приложенных к точкам A и B. Эти силы равны по абсолютной величине, противоположны по направлению и их линии действия совпадают с прямой AB. В результате получим эквивалентную систему сил, состоящую из , приложенных к A, и , приложенных к B.
3. Сложим силы и по правилу параллелограмма: . Тоже самое проделаем с и : . В результате получим эквивалентную систему сил, состоящую из и , приложенных к точкам A и B, соответственно. Эти силы составляют углы с прямой AB:
(4.1)   ,
где .
4. Найдем точку D пересечения линий действия сил и , и перенесем в D точки приложения этих сил. В результате получим эквивалентную систему сил, состоящую из и , приложенных к точке D.
5. Сложим и по правилу параллелограмма. В результате получим эквивалентную систему сил, состоящую из одной силы . Легко показать, что :
.
Поскольку силы и перпендикулярны AB, то равнодействующая также перпендикулярна AB. Если , то . Если , то . В общем случае,
.
6. Наконец, перенесем точку приложения равнодействующей вдоль ее линии действия в точку C, чтобы точки A, B и C располагались на одной прямой. Применяя (4.1), из прямоугольников ACD и BCD находим:
;
;
;

;

.
Пусть , тогда , точка C находится слева от A,

.
Пусть , тогда , точка C находится справа от B,

.

Определение равнодействующей, используя уравнения статики

Напомним, что равнодействующая – это одна сила, действие которой эквивалентно действию заданной системы сил. То есть законы движения твердого тела должны сохранить свой вид при замене заданной системы сил на равнодействующую. В уравнения движения твердого входит только векторная сумма внешних сил и сумма моментов этих сил относительно любой точки. Поэтому, при замене системы сил на равнодействующую, должны выполняться два условия.
1. Векторная сумма внешних сил должна равняться равнодействующей:
(5.1)   .
2. Сумма моментов внешних сил относительно произвольной точки O должна равняться моменту от равнодействующей силы относительно этой точки:
(5.2)   .
Здесь – момент равнодействующей , приложенной в точке C, относительно точки O; – момент силы , приложенной в точке A_i, относительно точки O. Моменты можно выразить посредством векторного произведения: , где – радиус вектор, проведенный из точки O в A_i. Тогда последнее уравнение можно записать так:
(5.3)   .

Эквивалентные преобразования сил применяются только для сил, приложенных к абсолютно твердому телу, или к системе тел, которая, согласно принципу отвердевания, может рассматриваться как твердое. Нельзя производить преобразования сил, приложенных к различным точкам и телам, которые могут совершать относительное движение.

Сонаправленные силы

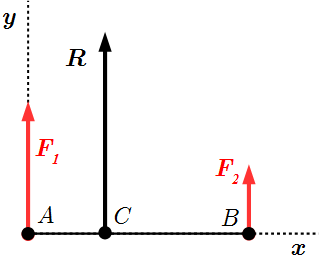
Переместим точки приложения сил и вдоль их линий действия в точки A и B так, чтобы отрезок AB был перпендикулярен направлениям сил. Выберем систему координат Axy с началом в точке A. Ось Ax направим от A к B; ось Ay – вдоль направлений сил.

Предположим, что равнодействующая сонаправлена силам и приложена в точке .

Спроектируем уравнение (5.1) на ось y.
.
Спроектируем уравнение (5.2) на ось Az, проходящей через точку A перпендикулярно плоскости рисунка.
(6.1)   .
Сила проходит через ось Az. Поэтому ее момент равен нулю: . Поскольку и , то отрезки AC и AB будут плечами сил и . Находим их моменты как произведения плеча силы на абсолютное значение:
.
Подставляем в (6.1):
;
.
Тем самым мы получили формулу (1.3), после чего легко получить остальные формулы.

Противоположно направленные силы

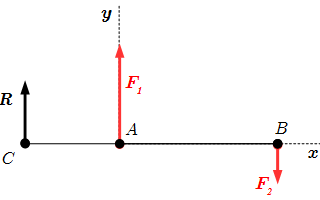
Как и в предыдущем случае, выберем систему координат Axy с началом в точке A. Считаем, что . Предполагаем, что равнодействующая сонаправлена с и приложена в точке C, находящейся на прямой AB, слева от точки A. Спроектируем уравнение для сил (5.1) на ось y.
.
Спроектируем уравнение для моментов сил (5.2) на ось Az, проходящей через точку A перпендикулярно плоскости рисунка.
(7.1)   .
Сила проходит через ось Az. Поэтому ее момент равен нулю: . Поскольку и , то отрезки AC и AB будут плечами сил и . Находим их моменты как произведения плеча силы на абсолютное значение:
.
Подставляем в (7.1):
;
.
И мы получили (2.3).

Вывод общей формулы

Пусть две параллельные силы и приложены к твердому телу в точках A и B. Найдем равнодействующую и точку ее приложения C, применяя уравнения (5.1) и (5.3).

Вектор равнодействующей равен сумме векторов сил, действующих на тело:
.

Теперь найдем точку приложения C равнодействующей из уравнения моментов (5.3). Для этого выберем прямоугольную систему координат с началом в произвольной точке O. Тогда момент равнодействующей относительно начала координат O должен равняться сумме моментов сил относительно этой точки:
(8.1)   .
Здесь – радиус векторы точек A, B и C. То есть векторы, проведенные из начала системы координат O к этим точкам.

Введем единичный вектор , направленный вдоль равнодействующей:
.
Выразим проекции векторов и на направление равнодействующей через скалярное произведение векторов:
,
.
Поскольку все силы параллельны, то
.
Тогда
;

.
Подставляем в (8.1).
.
Отсюда
,
где – произвольная постоянная.

Автор: Олег Одинцов.     Опубликовано: 29-11-2023