Определение реакций опор твердого тела – решение задачи

Приводится решение задачи, в которой требуемая реакция опоры твердого тела определяется из одного уравнения, без определения остальных сил реакций. Для трех вариантов закрепления тела выбирается тот, при котором требуемая реакция имеет наименьшее значение. Для этого варианта определяются реакции остальных опор.

Решим задачу на определение реакций опор твердого тела. Методы расчета реакций опор изложены на странице
Как определить реакции опор твердого тела

Задача на определение реакций опор твердого тела

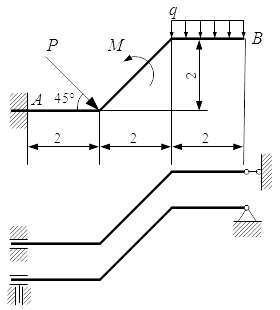
Твердое тело представляет собой ломаный брус. Показаны три способа его закрепления. Внешние силы и размеры одинаковы для всех способов закрепления. Определить реакции опор для того способа закрепления, при котором момент M_A в опоре A имеет наименьшее абсолютное значение.

Дано:
P = 5 kН; M = 8 kН·м; q = 1,2 kН/м.

Решение задачи

Схема 1

Рассмотрим схему 1. Проводим систему координат Axyz с началом в точке A. Ось Az перпендикулярна плоскости рисунка и направлена на нас.

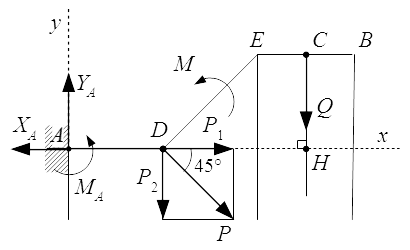
Опора A представляет собой жесткую заделку. Отбросим ее и заменим силами реакций. Силы реакций удобно разложить на три составляющие: на две силы и , параллельные осям координат; и на момент (пару сил) M_A.

Заменим равномерно распределенную нагрузку q равнодействующей . Абсолютное значение равнодействующей равно площади эпюры:
kН.
Точка приложения равнодействующей находится в центре тяжести эпюры – в точке C, посередине отрезка EB:
EC = CB = 1 м.

Итак, мы имеем три неизвестные величины: силы X_A, Y_A и момент M_A. Нам нужно определить только одну из них – это момент M_A. Заметим, что если мы будем определять моменты относительно оси Az, то моменты от сил X_A и Y_A обратятся в нуль, поскольку они пересекают эту ось. Тогда мы получим уравнение, содержащее только одну неизвестную: M_A.

Разложим силу на составляющие вдоль осей координат:
.
Абсолютные значения составляющих:
;   .

Находим моменты сил относительно оси Az. По правилу правого винта, положительным направлением является направление против часовой стрелки.
Силы , и пересекают ось A. Поэтому их моменты равны нулю:
;   ;   .
Сила перпендикулярна плечу AD. Ее момент:
.

Проводим прямую через вектор . Из точки A опускаем перпендикуляр AH на эту прямую. Отрезок AH является плечом силы . Он лежит на оси Ax. Момент силы :
.

Составляем уравнение равновесия. Сумма моментов сил, действующих на тело относительно оси Az равна нулю:
;
;
.
Отсюда

кН·м.

Итак, в первом варианте закрепления тела, момент в заделке A равен
кН·м.

Схема 2

Рассмотрим схему 2.

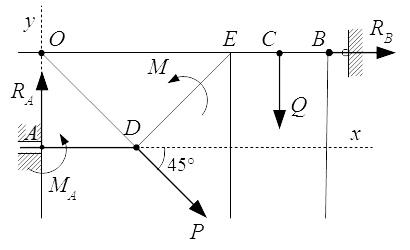
Опора A представляет собой скользящую заделку. Отбросим ее и заменим силами реакций. Силы реакций имеют две составляющие: силу , направленную вдоль оси Ay; и момент M_A.
Опора B представляет собой подвижный цилиндрический шарнир. Его реакцией является сила , направленная горизонтально.

Итак, мы имеем три неизвестные величины: силы R_A, R_B и момент M_A. Нам нужно определить только момент M_A. Проведем прямые через векторы и . Пусть O – точка пересечения этих прямых. Через эту точку проведем ось Oz′, перпендикулярно плоскости рисунка. Мы будем определять моменты относительно оси Oz′. Поскольку силы и пересекают эту ось, то их моменты равны нулю. Поэтому уравнение для моментов будет содержать только одну неизвестную: M_A.

Заметим, что из построения, угол . Тогда вектор пересекает ось Oz′. Поэтому момент от этой силы равен нулю.

Плечом силы является отрезок OC. Тогда момент равен
.

Составляем уравнение равновесия. Сумма моментов сил, действующих на тело относительно оси Oz′ равна нулю:
;
;
.
Отсюда
кН·м.

Итак, во втором варианте закрепления, момент в заделке A равен
кН·м.

Схема 3

Рассмотрим третий вариант закрепления тела.

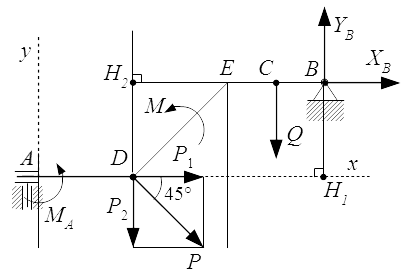
Опора A представляет собой бискользящую заделку. Реакцией здесь является момент (пара сил) M_A.
В шарнире B разложим силу реакции на составляющие и вдоль осей координат.

Будем определять моменты относительно оси Bz′′, проходящую через точку B перпендикулярно плоскости рисунка. Тогда моменты от сил X_B и Y_B обратятся в нуль, поскольку они пересекают эту ось. И мы получим уравнение, содержащее только одну неизвестную M_A.

Также, как и в первом случае, разложим силу на составляющие вдоль осей координат:
;
;   .

Находим моменты сил относительно оси Bz′′.
Плечом силы является отрезок CB = 1 м. Поэтому
.

Проведем прямую через вектор . Она совпадает с осью Ax. Из точки B опустим на нее перпендикуляр BH₁. Тогда BH₁ будет плечом силы . Ее момент:
.

Точно также проводим прямую через вектор и из точки B опускаем на нее перпендикуляр BH₂. Тогда BH₂ является плечом силы .
.

Составляем уравнение равновесия. Сумма моментов сил, действующих на тело относительно оси Bz′′ равна нулю:
;

;
.
Отсюда


кН·м.

Для третьего варианта,
кН·м.

Определение остальных реакций

Сравнивая найденные значения момента M_A для трех способов закрепления тела, находим, что момент имеет наименьшее значение для второй схемы. Для этой схемы определяем значения остальных реакций.

Составляем уравнения равновесия. Сумма проекций сил на ось x равна нулю:
;
;
.
Отсюда
кН.
Знак “минус” указывает на то, что реакция R_B направлена в сторону, противоположную той, что указана на рисунке.

Сумма проекций сил на ось y равна нулю:
;
;
.
Отсюда
кН.

Ответ

Момент M_A имеет наименьшее значение для второго способа закрепления тела. Реакции опор, для этого способа закрепления, имеют следующие величины:
кН;   кН;   кН·м.

Использованная литература:
Сборник заданий для курсовых работ по теоретической механике, под редакцией проф. А.А. Яблонского, Москва «Интеграл-пресс», 2006.

Автор: Олег Одинцов.     Опубликовано: 30-10-2017   Изменено: 06-01-2022