Аксиома связей (принцип освобождаемости от связей)
Аксиома связей
Аксиома связей (принцип освобождаемости от связей)
Всякое несвободное тело можно рассматривать как свободное, если действие связей заменить силами, называемыми силами реакций связей.
Аксиома связей, или, как ее еще называют принцип освобождаемости от связей, заключается в том, что мы отбрасываем связи, и вместо них вводим силы и (или) моменты сил. То есть, заменяем связи на силы, которые называются пассивными силами или силами реакций.
Более подробно связи рассматриваются на странице
Понятие механических связей и их классификация.
Виды связей и соответствующие им силы реакций приводятся на странице
Связи и их реакции в технической механике.
Ниже мы рассматриваем несколько примеров применения аксиомы связей.
Сама аксиома связей не является аксиомой как таковой, а является следствием дифференциальных уравнений движения точек механической системы. Выделение принципа освобождаемости от связей в отдельную аксиому имеет историческую причину.
Связи можно рассматривать как ограничения на возможные перемещения тела или материальной точки, вызванные взаимодействием с другими телами или точками. С математической точки зрения связи являются уравнениями или неравенствами, связывающие координаты и скорости точек системы.
Согласно фундаментальным законам механики, причиной возникновения ускорений точек являются действующие на них силы. Обычно сначала мы вводим силы, а по ним вычисляем траектории движения точек системы. Наличие связей несколько меняет ситуацию. При наложении связей мы заранее задаем либо законы движения некоторых точек, либо налагаем на координаты и скорости системы определенные условия.
Но основными фундаментальными законами механики являются дифференциальные уравнения движения точек системы, в которых ускорения точек определяются действующими на них силами (второй закон Ньютона). Тогда, чтобы выполнялись предварительно введенные ограничения в виде связей, мы должны ввести дополнительные силы, обеспечивающие выполнение уравнений связей. Такие силы выделяются в отдельную группу; они называются реакциями связей. Реакции связей не заданы изначально, а их значения определяются из уравнений связей. По этой причине их называют пассивными силами.
Определения
Приведем определения некоторых терминов, используемых в формулировке аксиомы связей.
- Связи
- – это ограничения на возможные перемещения тела или материальной точки, вызванные взаимодействиями с другими телами или точками. С математической точки зрения, связи являются уравнениями или неравенствами, связывающие координаты и скорости точек механической системы, а также время.
- Свободное тело
- Тело называется свободным, если на его перемещение не наложены связи, то есть если его перемещение ничем не ограничено.
- Несвободное тело
- Тело называется несвободным, если на его перемещение наложена одна или несколько связей, то есть если его перемещение ограничено другими телами.
- Силы реакций связей
- – это силы, добавляемые в систему для того, чтобы выполнялись условия связей. Говорят, что они являются силами, с которыми связи действуют на данное тело. Их также называют пассивными силами.
- Активные силы
- – это силы, действующие на тело, которые не являются силами реакций связей, то есть не являются пассивными силами.
Разделение сил на активные и пассивные является следствием причины их возникновения. Активные силы, как правило, известны и не зависят от наложенных на систему связей. Пассивные силы мы вводим для того, чтобы их действие приводило к соблюдению условий связей. Пассивные силы заранее неизвестны, они полностью определяются уравнениями связей. Хотя их направления часто определяются видом связи, но абсолютные величины зависят от действия других сил.
Кроме этого, пассивные силы никогда не являются причиной движения механической системы. Система начинает движение именно благодаря действию активных сил.
Аксиома связей в статике
Одной из самых востребованных задач в механике является задача на равновесие конструкции, находящейся под действием внешних сил. Элементы такой конструкции представляют собой систему соединенных между собой тел, закрепленных на опорах к неподвижному основанию. Виды опор подбираются таким образом, чтобы система и ее элементы находились в покое. Требуется найти силы, действующие в опорах и отдельных элементах конструкции.
С математической точки зрения, опоры и узлы, соединяющие отдельные элементы конструкции между собой, являются связями, поскольку они препятствуют свободному перемещению элементов конструкции. Таким образом, в статике мы имеем дело с системой тел со связями, все элементы которой находятся в покое. Для определения сил, действующих в опорах и узлах, мы применяем аксиому о связях. То есть, освобождаем все элементы системы от связей, и прикладываем вместо них силы реакций. Тем самым получаем систему, состоящую из свободных, не связанных между собой тел. На эту систему кроме заданных активных сил, также действуют и пассивные силы реакций, которыми заменены связи. Далее мы определяем величины пассивных сил так, чтобы система находилась в состоянии покоя.
Пассивные силы могут включать в свой состав также и пары сил (моменты). Направления пассивных сил и моментов зависят от вида применяемой связи. См. Связи и их реакции в технической механике. Заменив связи реакциями, каждый элемент конструкции становится свободным телом или свободной материальной точкой. Абсолютные значения реакций и их компонент находятся из условий равновесия. То есть мы подбираем величины реакций таким образом, чтобы каждый элемент системы, рассматриваемый как свободное тело, покоился.
Зависимость между отдельными телами системы осуществляется за счет применения закона действия и противодействия (3-й закон Ньютона). Согласно этому закону, реакция, с которой первое тело действует на второе, равна по абсолютной величине и противоположна по направлению реакции, с которой второе тело действует на первое. Таким образом, реакции, возникающие в точке соединения двух элементов конструкции связаны между собой: они равны по абсолютной величине и противоположны по направлению.
Далее мы рассмотрим несколько примеров применения принципа освобождаемости от связей.
Примеры применения аксиомы связей
Ломаный брус
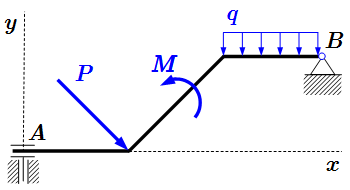
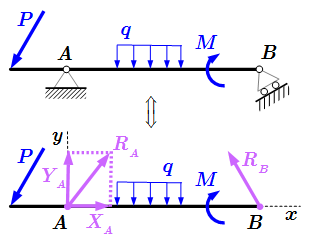
Рассмотрим плоскую конструкцию, в которой на ломаный брус AB действуют сила P, равномерно распределенная нагрузка q и момент силы M. Опора A – бискользящая заделка; опора B – неподвижный шарнир.
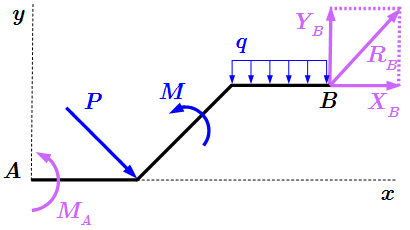
Освобождаемся от связей, вводя вместо них реакции. Опора A является бискользящей заделкой. В ней точка A, принадлежащая брусу может свободно перемещаться как по вертикали, так и по горизонтали. Поскольку препятствия перемещения точки A нет, то сила реакции в ней отсутствует. Но в заделке фиксировано направление конца бруса. То есть он не может поворачиваться относительно центра поворота в точке A. При попытке поворота, возникает препятствие вращению в виде момента сил, который мы обозначим как . Поскольку задача плоская, то пара сил с моментом лежит в плоскости рисунка, а вектор момента – перпендикулярен этой плоскости. Здесь – единичный вектор, направленный вдоль оси системы координат. Эта ось перпендикулярна плоскости рисунка и направлена на нас.
Опора B является неподвижным шарниром. В ней точка B, принадлежащая брусу не может свободно перемещаться как по вертикали, так и по горизонтали. При попытке перемещения, возникает сила, препятствующая этому перемещению. Поэтому в точке B имеется сила реакции , которая может иметь произвольное направление. Ее удобно разложить на составляющие , направленные вдоль осей координат. Здесь – единичные векторы, направленные вдоль осей системы координат. Величины являются проекциями на оси координат. Они могут принимать положительные, отрицательные или нулевые значения. Если какая-либо из этих величин отрицательна, то соответствующей ей вектор или направлен противоположно оси координат. Абсолютная величина силы реакции:
.
Поскольку в шарнире B не происходит препятствия вращению закрепленного конца, то в реакцию связи в точке B момент сил не входит.
Таким образом, конструкция со связями, изображенная на верхнем рисунке, эквивалентна конструкции, в которой связи заменены реакциями. Всего имеется три величины реакции: . Поскольку задача плоская, то имеется три линейно независимых уравнения равновесия, из которых можно определить значения этих реакций.
Составная конструкция
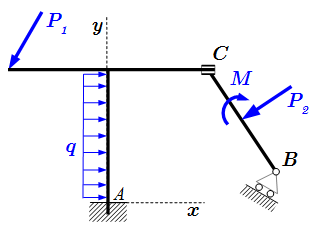
Рассмотрим составную конструкцию, состоящую из рамы AC и стержня CB. На конструкцию действуют силы , равномерно распределенная нагрузка q и пара с моментом M. Опора A – жесткая заделка; в точке B – опора на катках. Рама и стержень соединены скользящей заделкой в точке C.
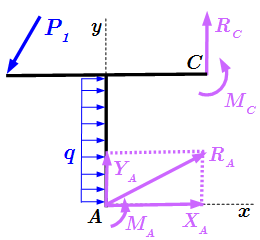
Освобождаемся от связей. Рассмотрим раму AC. Опора A является жесткой заделкой. В ней точка A, принадлежащая раме, не может перемещаться ни по вертикали, ни по горизонтали. Поэтому в состав реакций входит сила , имеющая произвольное направление, действие которой направлено на препятствие перемещению. Ее удобно разложить на составляющие , направленные вдоль осей координат:
.
Здесь – единичные векторы, направленные вдоль осей координат; – проекции вектора на оси координат. Проекции могут иметь как положительные, так и отрицательные значения. В случае отрицательного значения, соответствующая составляющая направлена противоположно оси координат.
Поскольку в жесткой заделке, рама не может поворачиваться относительно центра вращения A, то в реакцию также входит момент , препятствующий повороту вокруг A. Вектор момента направлен перпендикулярно плоскости фигуры:
.
Здесь – единичный вектор вдоль оси z, которая перпендикулярна плоскости фигуры и направлена на нас; – проекция момента на ось z. Если , то вектор направлен вдоль оси z. На рисунке это соответствует закручиванию против часовой стрелки. Если , то направлен противоположно оси z – закручивание по часовой стрелке.
Таким образом, реакция в жесткой заделке A представлена силой и моментом . Она задается тремя числами , которые могут иметь положительные, отрицательные или нулевые значения.
Узел C является скользящей заделкой. В нем точка C, принадлежащая раме, может свободно перемещаться вдоль направляющей, которая направлена вдоль оси x, но не может перемещаться в перпендикулярном направлении – вдоль оси y. Кроме этого, рама не может поворачиваться относительно центра C. Поэтому реакция в точке C представлена силой и моментом .
Таким образом, реакция в скользящей заделке C задается двумя числами , которые могут иметь положительные, отрицательные или нулевые значения.
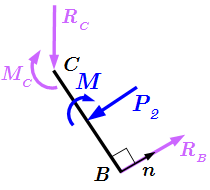
Рассмотрим стержень CB. Согласно закону действия и противодействия, силы, действующие на стержень в узле C со стороны рамы, равны по величине и противоположны по направлению силам, действующим в этом узле на раму со стороны стержня. Поэтому реакция в узле C состоит из силы и момента .
Опора в точке B является опорой на катках. В ней точка B может свободно перемещаться вдоль поверхности, но не может перемещаться в перпендикулярном направлении. Поэтому возникает сила реакции , направленная перпендикулярно поверхности:
,
где – единичный вектор нормали к поверхности.
Поскольку стержень может свободно поворачиваться относительно центра B, то момент сил, препятствующий повороту, отсутствует. Поэтому реакция в точке B состоит из одной силы .
Таким образом, составная конструкция со связями, изображенная на верхнем рисунке эквивалентна двум свободным телам – раме и стержню, в которых связи заменены реакциями. Мы нашли, что всего имеется шесть величин, определяющих реакции в точках соединений: . Поскольку задача плоская, то для каждого тела можно составить по три линейно независимых уравнения равновесия – всего шесть уравнений, из которых можно определить шесть неизвестных: .
Плита, поддерживаемая стержнями
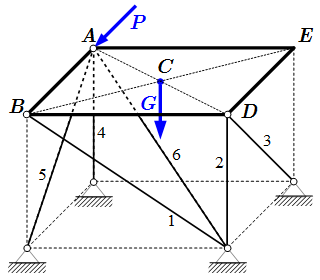
Рассмотрим прямоугольную однородную плиту ABDE, на которую действуют сила тяжести G и заданная сила P. Плита поддерживается невесомыми жесткими стержнями 1, 2, 3, 4, 5, 6, концы которых закреплены шарнирами.
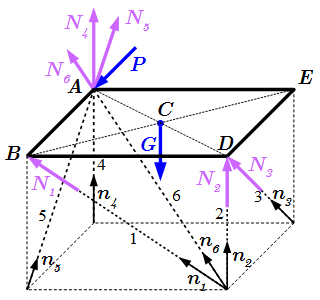
Освобождаемся от связей. Реакцией жесткого невесомого стержня с номером i является сила , направленная вдоль стержня, от одного конца к другому. Отбрасываем все стержни, а в точке крепления i-го стержня к плите, вводим силу реакции
.
Здесь – единичный вектор, направленный вдоль стержня. На рисунке мы выбрали направления этих векторов таким образом, что если , то i-й стержень сжат; если , то растянут. Правда, в сопротивлении материалов, такой выбор знаков в величинах не является общепринятым. Там принято, что если усилие в стержне положительно, то он растянут, а если отрицательно, то сжат. Но для нас это не имеет значения.
Таким образом, плита со связями в виде стержней, изображенная на верхнем рисунке, эквивалентна плите, в которой связи заменены реакциями. Всего имеется шесть величин реакций: . Поскольку конструкция трехмерная, то имеется шесть линейно независимых уравнений равновесия, из которых можно определить шесть значений усилий в стержнях.
Использованная литература:
Н. Н. Бухгольц. Основной курс теоретической механики, часть 1. Москва, «Наука», 1965.
Автор: Олег Одинцов. Опубликовано:
