Способы расчета момента силы относительно точки и оси
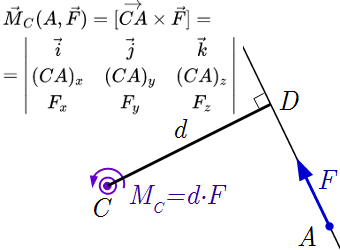
Определение момента силы относительно точки
Чтобы найти момент силы , приложенной в точке A, относительно точки C, нужно найти векторное произведение [CA × F]:
(1) ,
где – единичные векторы в направлении осей прямоугольной системы координат Oxyz. Это можно сделать двумя способами – координатным и геометрическим.
Координатный способ
Координатным способом мы находим проекции вектора момента на оси произвольной прямоугольной системы координат Oxyz. Они определяются по формулам векторного произведения :
(2)
.
Здесь ; – радиус векторы и координаты точек C и A; – проекции вектора силы на оси координат. Модуль момента (абсолютное значение):
.
Если нужно найти момент силы относительно начала координат O, то , и предыдущие формулы будут иметь более простой вид:
(3) .
Геометрический способ
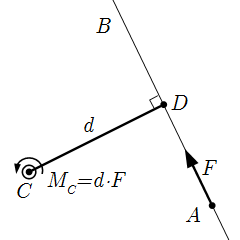
Геометрическим способом мы находим модуль момента силы как произведение модуля силы на ее плечо относительно точки C.
.
Вектор момента направлен перпендикулярно плоскости, в которой лежат точки C, A и вектор . Направление определяется по правилу правого винта: если приложить винт перпендикулярно указанной плоскости к точке C, и вращать в направлении , то шляпка винта будет перемещаться в направлении момента .
Плечо силы относительно точки C – это расстояние между точкой C и линией действия AB силы . Для его определения, из точки C нужно опустить перпендикуляр на линию действия силы до пересечения в точке D.
Линия действия силы – это прямая, проведенная через точку A ее приложения, параллельно вектору силы .
Упрощение расчетов
В некоторых случаях расчеты можно упростить, если воспользоваться свойствами момента силы относительно точки. Перечислим их.
Момент силы относительно любой точки не изменится, если точку приложения силы переместить вдоль ее линии действия.
Силу можно разложить по правилу параллелограмма:
.
Момент от векторной суммы сил, приложенных к одной точке равен векторной сумме моментов этих сил, приложенных к этой точке:
.
Если линия действия силы проходит через точку C, то ее момент относительно этой точки равен нулю.
Предостережения

1. С математической точки зрения, любой трехмерный вектор представляет собой три числа , которые являются проекциями этого вектора на оси координат. Геометрически это означает, что начало любого вектора всегда совпадает с началом системы, а координаты его конца являются искомыми проекциями . Однако в механике часто изображают силу, приложенную к некоторой точке. То есть под силой подразумевают не один, а совокупность двух векторов – вектора силы и радиус вектора ее точки приложения. Тогда для определения проекций силы, нам нужно мысленно построить новую систему координат Axyz с началом в точке приложения A и осями, параллельными Ox, Oy и Oz имеющейся системы. Координаты конца вектора , в системе Axyz, и являются проекциями силы в системе координат Oxyz.
Также можно ввести единичные векторы , направленные вдоль осей . Тогда
.
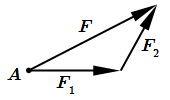
2. Разложение силы по правилу параллелограмма часто изображают так, как показано на первом рисунке.
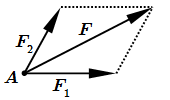
Однако, при вычислении моментов, компоненты следует откладывать из одной точки.
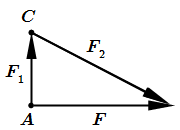
Пример. Разложим силу на составляющие и как показано на рисунке. Линии действия и проходят через точку C. Значит, их моменты относительно этой точки равны нулю. Тогда и момент силы относительно C должен равняться нулю. Но это не верно.
Почему так получается?
3. Момент силы всегда определяется относительно наперед выбранной точки. Если такая точка не указывается, то под ней подразумевается начало системы координат.
Определение момента силы относительно оси
Моментом силы относительно оси называется проекция вектора момента силы, определенного относительно любой точки, принадлежащей оси, на направление этой оси.
См. Определение и свойства момента силы отностельно оси.
1. Моментами силы относительно осей Ox, Oy, Oz прямоугольной системы координат Oxyz являются, указанные в (3), проекции момента относительно начала O:
.
В этом заключается один из способов определения осевого момента. Чтобы найти момент силы относительно оси CC', нужно выбрать прямоугольную систему координат так, чтобы одна из осей совпадала с CC'. Тогда по одной из формул (3) можно найти величину осевого момента. Допустим, что мы выбрали систему координат Oxyz, у которой CC' совпадает с осью Oz. Тогда момент силы относительно оси CC' определяется по формуле:
.
2. Если такую систему координат выбрать затруднительно, то можно выполнять расчеты в любой прямоугольной системе координат. Для этого, по формулам (2) находим проекции момента силы относительно любой точки C, принадлежащей оси CC'. Далее находим проекции единичного направляющего вектора этой оси. Искомая проекция вектора на направление CC' равна скалярному произведению векторов и :
.
Для определения , выберем две точки, принадлежащие оси. Обозначим их как и . Пусть положительным направлением будет направление от C к B. Тогда вектор , проведенный из C к B, будет направляющим вектором оси. Находим его проекции и длину:
;
; .
Нормируя, получаем координаты направляющего вектора единичной длины:
.
3. В более простых способах можно определять осевой момент геометрическим способом. Для этого нужно выбрать плоскость, перпендикулярную оси, спроектировать на нее силу и точку ее приложения. И далее найти момент как для плоской задачи.
Упрощение расчетов осевого момента
Иногда можно упростить расчеты, если воспользоваться некоторыми свойствами осевого момента.
Момент силы не изменится, если точку приложения силы переместить вдоль ее линии действия.
Силу , приложенную к точке A можно разложить на составляющие по правилу параллелограмма: . Тогда момент относительно оси CC' будет равен сумме моментов от сил и , приложенных к точке A:
.
Момент силы относительно оси равен нулю,
⚫ если линия действия силы пересекает ось,
⚫ если сила параллельна оси.
Определение момента силы в плоских задачах
В плоской задаче состояние системы описывается в двухмерной системе координат. Пусть это будет прямоугольная система Oxy. Сила и все точки расположены в этой плоскости, как говорят, в плоскости фигуры. Но момент силы определяется в трехмерной системе. Поэтому мысленно проводим ось Oz перпендикулярно плоскости фигуры, чтобы получить трехмерную прямоугольную правую систему координат. Момент силы будет иметь только одну проекцию на эту ось. Проекции на другие оси равны нулю. То есть вектор момента всегда перпендикулярен плоскости фигуры. В этом случае величину называют алгебраическим значением момента. Алгебраическое значение момента в плоских задачах обычно обозначают строчной буквой:
.
Пример расчета момента силы в плоской задаче
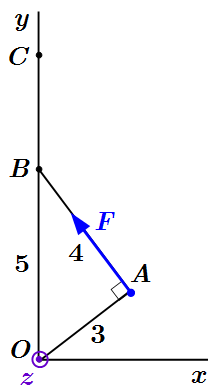
Рассмотрим пример определения момента силы в плоской задаче. Пусть сила Н приложена в точке A параллельно AB, как показано на рисунке. |OA| = 3 м, |AB| = 4 м, |OB| = 5 м, |BC| = 3 м; . Найдем момент силы относительно точек O и C.
Мысленно проведем ось Oz. Она перпендикулярна плоскости рисунка и направлена на нас. В результате получилась трехмерная правая прямоугольная система координат.
Прямая, проходящая через точки A и B, является линией действия силы . Поскольку , то OA – плечо силы относительно точки O. Тогда мы можем найти абсолютное значение момента относительно точки O:
Нм.
Если мы приложим правый винт к точке O параллельно оси Oz, и будем вращать его в направлении , то шляпка винта будет перемещаться на нас, то есть в направлении оси Oz. Поэтому величина положительна. Тем самым мы нашли алгебраическое значение момента силы относительно начала координат O:
Нм.
Находим момент силы относительно точки C (рисунок ниже):
Нм.
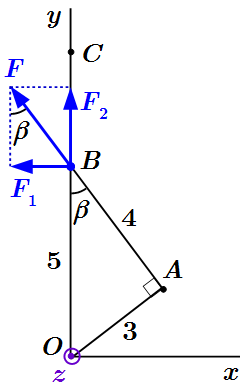
Сделаем пояснения. Воспользуемся тем, что момент не меняется при перемещении точки приложения силы вдоль ее линии действия:
.
Переместим точку приложения силы в B, и разложим ее по правилу параллелограмма на компоненты, параллельные осям координат:
.
Тогда момент равен векторной сумме моментов компонент:
.
Спроектируем это векторное уравнение на ось z и изменим обозначения:
;
.
Линия действия силы совпадает с осью Oy, и пересекает точку C. Поэтому ее момент равен нулю:
.
Поскольку , то отрезок BC будет плечом силы . Находим модуль момента:
.
Если зафиксировать точку C, то сила будет закручивать фигуру по часовой стрелке. Тогда, по правилу правого винта, ,
.
Найдем модуль силы F1. Параллелограмм сил является прямоугольником. Поэтому
.
Здесь синус угла находится из прямоугольника OAB: .
В результате получаем:
Нм.
Пример определения момента силы в пространстве
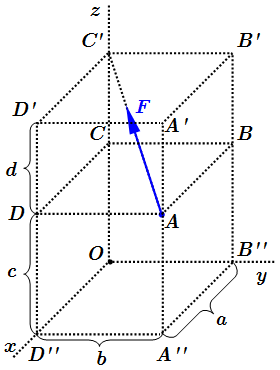
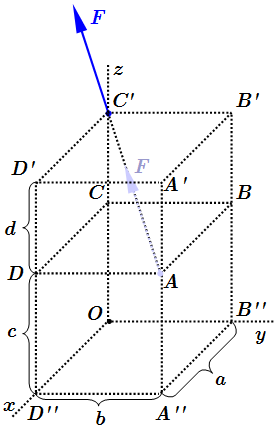
Найти момент силы , приложенной к точке A как показано на рисунке относительно начала координат O. Найти момент этой силы относительно осей DB и DB'.
Расчет момента относительно точки O
;
(П2.1) ,
,
,
;
;
;
;
;
;
.
Сделаем пояснения по поводу расчетов проекций силы на оси координат. Они вычисляются так:
.
Из прямоугольных треугольников C'AB,C'AD и C'AA' имеем:
.
Длину диагонали AC' прямоугольного параллелепипеда вычисляем по теореме Пифагора:
.
Более простое решение
Можно упростить расчеты, воспользовавшись перечисленными выше свойствами.
Поскольку линия действия силы пересекает ось , то .
Переместим точку приложения силы вдоль ее линии действия в точку C'. Момент от этого не изменится:
.
Проекции силы на оси координат останутся прежними, они определяются формулами (П2.1). Две координаты точки приложения силы равны нулю:
.
Вычисляем оставшиеся проекции момента:
;
;
.
Расчет момента относительно осей
Поскольку диагонали параллелепипеда пересекаются, то линия действия силы F пересекает ось DB'. Поэтому ее момент относительно этой оси равен нулю:
.

Найдем момент силы относительно оси DB. Для этого нужно найти момент относительно любой точки, принадлежащей этой оси, и спроектировать момент на ее направление.
Возьмем точку D и вычислим относительно нее момент силы.
.
Проекции силы мы нашли ранее, см. (П2.1).
;
;
(линия действия AC' силы F пересекает ось Dy);
;
.
Найдем проекции единичного направляющего вектора оси DB. Для этого выберем на оси две точки. Пусть это будут точки D и B. Положительное направление оси – от D к B. Определяем проекции вектора на оси координат:
.
Длина вектора:
.
Проекции единичного направляющего вектора на оси координат:
.
Определяем момент силы относительно оси DB как проекцию вектора на ось DB:
.
Ответ
;
;
.
Автор: Олег Одинцов. Опубликовано:
