Примеры решений однородных дифференциальных уравнений Эйлера

Рассмотрены примеры решений однородных дифференциальных уравнений Эйлера.

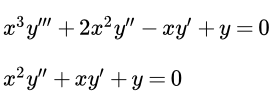
Здесь мы рассматриваем примеры решений однородных дифференциальных уравнений Эйлера. Методы решения уравнения Эйлера подробно рассмотрены на странице
«Дифференциальное уравнение Эйлера и методы его решения».

Пример 1

Решить уравнение
(1)   .

Решение

Ищем решение в виде
.
Находим производные:
;
;
.
Подставляем в (1):
.
Сокращаем на x^k и получаем характеристическое уравнение:
.

Выполняем преобразования.
;
;
;
;
;
.
Получаем три действительных корня:
.
Им соответствуют три линейно независимых решения:
.
Общее решение уравнения:

Ответ

.

Пример 2

Решить уравнение
(2)   .

Решение

Ищем решение в виде .
Находим производные:
;
.
Подставляем в (2):
.
Сокращаем на x^k и получаем характеристическое уравнение:
.

Выполняем преобразования.
;
;
.
Получаем два комплексных корня:
.
Им соответствуют два линейно независимых решения:
.
Общее решение уравнения:
.

Ответ

Автор: Олег Одинцов.     Опубликовано: 14-08-2013