Понятие механических связей и их классификация
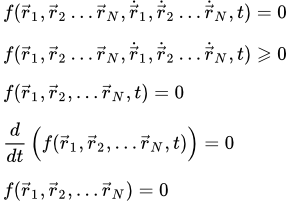
Понятие и определение связей в теоретической механике
- Связи
- – это уравнения или неравенства, связывающие координаты и скорости точек механической системы, а также время.
- Механическая система
- – это множество материальных точек или механических систем, в котором движение каждой точки зависит от положения и движения остальных точек системы.
- Свободная система
- – это механическая система, на элементы, из которых она состоит, не наложены связи.
- Несвободная система
- – это механическая система, на элементы, из которых она состоит, наложены одна или несколько связей.
Для чего нужны связи в механике
Возьмем простейшую механическую систему, состоящую из одних материальных точек. В качестве примера рассмотрим твердое тело. В общем случае, перемещения материальных точек в нем ничем не ограничены. Существуют только силы взаимодействия между точками, приводящие к тому, что при увеличении расстояний, возникают силы притяжения, а при уменьшении – силы отталкивания. В результате каждая точка совершает небольшие перемещения относительно своего положения равновесия. При этом точки могут сближаться и отдаляться друг от друга, что приводит к деформациям и колебаниям тела. Такая система является свободной.
Но существуют задачи, в которых нужно определить только законы движения тела, и при этом деформации, возникающие при движении, пренебрежимо малы. Тогда, чтобы упростить решение, вводят математические уравнения, в которых пренебрежимо малые величины просто приравнивают к нулю. Такие уравнения называются связями. Для твердого тела искусственным образом полагают, что относительные положения материальных точек жестко зафиксированы и не меняются со временем. То есть расстояние между любыми двумя точками является постоянной величиной. В результате мы получаем тело со связями, в котором материальные точки не являются свободными – их координаты связаны уравнениями. Тогда твердое тело, рассматриваемое как механическая система, становится несвободной механической системой, которая называется абсолютно твердым телом. Поскольку в теоретической механике не изучают деформации и колебания, то часто опускают термин «абсолютно». То есть под твердым телом в теоретической механике, как правило, подразумевается абсолютно твердое тело.
Далее мы можем конструировать механические системы не только из материальных точек, но и из абсолютно твердых тел и других механических систем. Например, можно рассматривать два тела, соединенные сферическим шарниром. Если нас не интересуют возникающие в шарнире деформации, то мы можем наложить на тела связь, которая заключается в том, что координаты точки первого тела в месте крепления шарнира равны координатам точки второго тела. Сферический шарнир связывает две точки, принадлежащие разным телам, но позволяет им вращаться в любом направлении. В результате два тела перестают быть свободными. И мы получаем новую систему, состоящую из двух твердых тел, соединенных сферическим шарниром. К этой системе можно с помощью связей присоединить новые тела или материальные точки, и получить новые, более сложные механические системы. И так далее.
Подчеркнем, что связи – это фиктивные уравнения или неравенства, наложенные на координаты и(или) скорости точек с целью упрощения математического решения задачи. В реальном теле всегда происходят смещения координат точек относительно положений равновесия и относительные расстояния между материальными точками меняются со временем. Но для некоторых задач эти смещения малы, и ими можно пренебречь. Тогда, чтобы упростить решение, вводят связи, то есть считают тело абсолютно твердым.
Виды механических связей и их классификация
Далее подразумевается, что система состоит из N материальных точек, координаты которых задаются радиус-векторами , а скорости – их производными по времени . Все это можно применить и к более сложной системе, положение которой определяется с помощью n обобщенных координат. Тогда вместо координат следует понимать набор обобщенных координат системы , а вместо скоростей – производные обобщенных координат по времени: .
Обобщенные координаты – это n независимых величин, которые полностью определяют положение системы. Так для твердого тела в качестве обобщенных координат можно взять декартовы координаты произвольным образом выбранной точки тела и три угла Эйлера , определяющих ориентацию тела относительно неподвижной системы координат. Обобщенные координаты можно выбирать различными способами.
- Удерживающей, двусторонней или неосвобождающей
- называется связь, препятствующая перемещению системы в двух направлениях. Она задается соотношением со знаком равенства:
.
- Неудерживающей, односторонней или освобождающей
- называется связь, препятствующая перемещению системы в одном направлении и допускающая перемещение в противоположном направлении. Она задается соотношением со знаком неравенства:
.
Пример удерживающей связи – два шарика, соединенных абсолютно жестким стержнем. Пример неудерживающей связи – два шарика, соединенных нерастяжимой нитью.
- Геометрической или конечной
- называется связь, в уравнение которой не входят скорости точек:
.
- Кинематической или дифференциальной
- называется связь, в уравнение которой входят скорости точек:
.
Всякую геометрическую связь можно продифференцировать по времени, и получить кинематическую:
(К1) .
Обратное не верно. Не любую кинематическую связь можно проинтегрировать и получить геометрическую.
- Интегрируемой
- называется дифференциальная связь, уравнение которой можно проинтегрировать, и получить уравнение геометрической связи, не содержащее скоростей точек.
- Неинтегрируемой
- называется дифференциальная связь, уравнение которой нельзя проинтегрировать и свести к геометрической связи. То есть уравнение неинтегрируемой связи при любых математических преобразованиях будет содержать производные координат по времени.
Чтобы проинтегрировать дифференциальную связь, ее нужно привести к виду (К1), после чего получаем геометрическую связь:
;
,
где C – постоянная интегрирования.
- Голономной
- называется геометрическая или кинематическая интегрируемая связь. То есть голономная связь может быть приведена к геометрической связи (которая не содержит скоростей).
- Голономной системой материальных точек
- называется система, содержащая только геометрические или кинематические интегрируемые связи. Голономная система не содержит неинтегрируемых кинематических связей. Поэтому она может быть приведена к системе, содержащей только геометрические (конечные) связи.
- Неголономной
- называется кинематическая неинтегрируемая связь.
- Неголономной системой материальных точек
- называется система, содержащая неинтегрируемые кинематические связи.
- Стационарной или склеромной
- называется голономная связь, уравнение которой не содержит время в явном виде. То есть стационарная связь может быть приведена к следующему виду:
.
- Нестационарной или реномной
- называется голономная связь, уравнение которой содержит время в явном виде.
- Обратимой или катастатической
- называется дифференциальная связь, уравнение которой не меняется при замене направлений всех скоростей на противоположные: . То есть если у системы только катастатические связи, то наряду с прямым движением допустимо зеркально симметричное движение в обратном направлении.
- Идеальной
- называется связь, силы реакции которой не совершают работу при виртуальных перемещениях системы. В противном случае связь называется неидеальной или реальной. Для стационарных связей виртуальные перемещения совпадают с возможными перемещениями, то есть с любыми изменениями координат системы, при которых не нарушаются уравнения связей. Для нестационарных связей виртуальные перемещения – это бесконечно малые изменения координат, при которых не нарушаются уравнения связей при фиксированном значении времени.
Как правило, неидеальные связи возникают вследствие возникновения трения между соприкасающимися частями конструкций. Например пусть тело лежит на абсолютно гладкой поверхности . Мы можем переместить его вдоль поверхности. Поскольку она абсолютно гладкая, то сила трения со стороны поверхности не возникает и наличие поверхности не приводит к совершению работы. Если рассмотреть шероховатую поверхность, то в месте сцепления возникает сила трения, препятствующая перемещению, которая совершает отрицательную работу. Поэтому при наличии трения связь перестает быть идеальной. Однако, ее можно свести к идеальной, если силу трения отнести к активным силам. То есть шероховатая поверхность эквивалентна абсолютно гладкой поверхности, если включить силы трения в состав внешних (активных) сил. Во всех случаях реальных связей их преобразуют к идеальным, включая силы трения в состав активных сил.
Примеры связей различных типов
Жесткий стержень
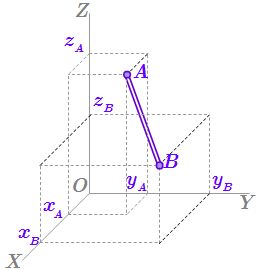
Рассмотрим два маленьких, не взаимодействующих между собой, шарика A и B, которые будем считать материальными точками. Их положения в пространстве определяются координатами и в предварительно выбранной системе координат. Теперь соединим их стержнем, длина которого в ненапряженном состоянии . В результате мы получим механическую систему, состоящую из двух материальных точек и стержня. Материал, из которого состоит стержень, обладает упругими свойствами. При движении шарики могут двигаться с ускорением, что приведет к возникновению усилий в стержне, в результате которых он будет укорачиваться, удлиняться или изгибаться. Такая система является свободной, поскольку шарики могут иметь любые координаты. Расстояние между ними может быть больше или меньше l.
Пусть стержень изготовлен из достаточно прочного материала, так что при движении системы, его длина изменяется на малую величину , не существенную для нашей задачи. Тогда в первом приближении мы можем игнорировать изменение длины и возможный изгиб стержня, полагая, что он прямолинейный и его длина постоянна и равна l. То есть мы можем положить . Математически это означает, что мы связываем координаты точек A и B уравнением:
(П1) .
Это уравнение является связью, которую мы наложили на систему. В результате она стала несвободной. Это двусторонняя геометрическая голономная стационарная связь. Применение связи позволило свести задачу к более простой. Но при этом мы исключаем из рассмотрения возможные деформации и колебания стержня.
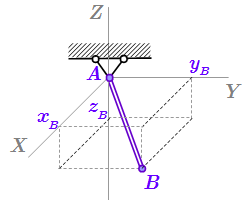
Если один конец A стержня закреплен сферическим шарниром на неподвижном основании, то координаты точки A будут фиксированы. Они не смогут изменяться со временем. Если закрепленная точка A находится в начале координат, то к уравнению (П1) добавятся еще три уравнения связи:
.
Это также двусторонние геометрические голономные стационарные связи.
Нерастяжимая нить
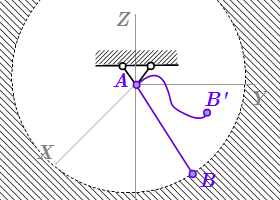
Если у нас вместо стержня нерастяжимая нить, то расстояние между точками A и B не могут быть больше длины нити l. Поскольку нить может беспрепятственно изгибаться, то расстояния между точками может быть меньше l. Тогда уравнение связи примет вид неравенства:
(П2.1) .
В отличии от жесткого стержня, это односторонняя связь.
Для применения такой связи, движение точки B нужно разбить на несколько временных интервалов. В одних интервалах нить будет натянута, и соотношение (П2.1) превратится в равенство:
(П2.2) .
Для других интервалов, нить будет изогнута и не будет оказывать влияния на движение точки B. На этих интервалах точка B будет свободной.
Лезвие конька на плоскости
Рассмотрим движение лезвия конька по ледяной поверхности. Будем считать поверхность плоской, абсолютно твердой и гладкой. Конек движется по направлению его лезвия. Перемещение в перпендикулярном направлении отсутствует. Будем рассматривать только плоское движение, при котором лезвие перпендикулярно поверхности льда. Выберем прямоугольную систему координат XYZ с началом, расположенным на поверхности. Тогда поверхность льда описывается уравнением .
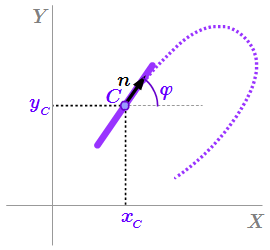
Положение конька, при наших ограничениях, полностью определяется четырьмя координатами . Из них – координаты его нижней точки C, соприкасающейся со льдом; – угол между направлением лезвия и осью X системы координат.
Составим уравнения связей для конька. Будем считать, что конек прижат ко льду. Так что не происходит его отрыва в вертикальном направлении. Это приводит к уравнению связи
(П3.1) .
Единичный вектор , направленный вдоль лезвия имеет следующие компоненты:
.
Поскольку перемещение конька происходит вдоль его лезвия, то скорость направлена вдоль вектора :
,
где – модуль скорости. Запишем это уравнение по компонентам:
.
Исключая модуль скорости, находим:
;
.
Наконец подставив , получим:
(П3.2) .
В это уравнение входят производные координат по времени. Поэтому это дифференциальная (или кинематическая) связь. Таким образом система связей при движении конька на плоскости описывается уравнениями (П3.1) и (П3.2).
Покажем, что связь (П3.2) неинтегрируемая. Предположим противное. Допустим, что она интегрируемая. Тогда с помощью эквивалентных преобразований, уравнение (П3.2) можно привести к виду
(П3.3) .
Раскрываем производную.
.
Сравнивая с (П3.2) имеем:
.
Здесь – функция от . Из последних двух уравнений заключаем, что f не зависит от и t. То есть является функцией только от и :
.
Тогда из первых двух уравнений находим:
.
Здесь левая часть не зависит от , а правая зависит. Возникло противоречие. Поэтому связь (П3.2) не может быть приведена к виду (П3.3). То есть она неинтегрируемая и поэтому неголономная.
Грузик между двигающимися плоскостями
Рассмотрим грузик, расположенный между двумя сцепленными плоскими поверхностями. Будем считать, что грузик является материальной точкой, а поверхности – абсолютно твердые и гладкие. Направим оси x и y неподвижной системы координат вдоль поверхности, ось z – перпендикулярно. Тогда движение груза вдоль осей x и y является свободным. По оси z перемещение ограничено. Пусть поверхности, в свою очередь, движутся вдоль оси z по закону . Тогда уравнение связи для грузика имеет вид:
(П4.1) .
Это удерживающая геометрическая голономная реномная связь. Это пример связи, уравнение которой зависит от времени. Поэтому она является нестационарной, или реномной.
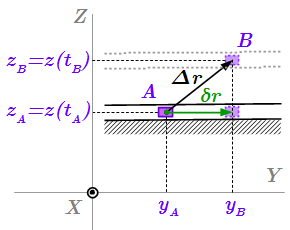
На этом примере проясним вопрос о возможных и виртуальных перемещениях системы. Возможное перемещение – это любое изменение координат системы, осуществляемые за конечный промежуток времени , при котором выполняются уравнения связей, наложенных на систему. Пусть в первый момент времени точка имела координаты . Поскольку на нее наложена связь (П4.1), то . Чтобы получить возможное перемещение точки, мы должны рассмотреть грузик в другой момент времени с любыми значениями координат . Единственное условие, накладываемое на координаты – они должны удовлетворять уравнениям связей. В нашем случае – это уравнение (П4.1). Из него . Таким образом, возможным перемещением грузика является вектор с компонентами:
.
Возможное перемещение содержит компоненту в направлении оси z: . Поскольку поверхности абсолютно гладкие, то сила реакции связи направлена вдоль оси z: . Таким образом при возможном перемещении грузика, она совершит работу , даже если поверхности абсолютно гладкие.
Теперь рассмотрим виртуальное перемещение грузика. Единственное отличие от возможного перемещения состоит в том, что изменение координат системы относится к одному и тому же моменту времени. Тогда чтобы получить виртуальное перемещение точки, мы должны рассмотреть грузик с любыми новыми значениями координат , но в тот же самый момент времени . Единственное условие, накладываемое на координаты системы заключается в том, что должны выполняться уравнения связей. В нашем случае это уравнение (П4.1). Из него находим:
.
Отсюда . Виртуальным перемещением грузика является вектор с компонентами:
.
Видно, что виртуальное перемещение не содержит компоненту в направлении оси z. Поэтому, если поверхность абсолютно гладкая, то при виртуальном перемещении грузика, сила реакции связи не совершает никакой работы.
Использованная литература:
А. П. Маркеев. Теоретическая механика. Редакция журнала «Регулярная и хаотическая динамика», Ижевск 1999.
Автор: Олег Одинцов. Опубликовано:
