Уравнения Гинзбурга - Ландау (ГЛ)

Уравнения Гинзбурга Ландау и их простейшие исследования. Безразмерные уравнения ГЛ. Вывод уравнения вариацией функционала. Калибровочная инвариантность.

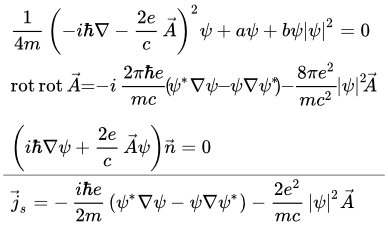
Сводные данные (постоянные и уравнения)

Примечание.
Под полем ^→H здесь и далее подразумевается истинное микроскопическое магнитное поле.
Носителем зарядов считаются куперовские пары – то есть два электрона. Заряд пары равен 2e ,  масса 2m ,  где e – заряд электрона; 2m – эффективная масса куперовской пары;

Чтобы убрать квадратный корень, можно еще сделать замену ^→A → √ 2  ^→A .  Тогда единицей магнитного поля станет √ 2  H_c  . 
^→r = λ^→r,  ^→H = √ 2  H_c ^→H,   ^→A = √ 2  λH_c ^→A . 
( – iϰ^– 1 ∇ – ^→A  ) ²  f  –  f  +  f  |  f  | ²  = 0 .
rot rot ^→A =  – i (2ϰ ) ^– 1 ( f ^* ∇ f  –  f ∇ f ^* )  –  |  f  | ^2 →A ; 
( ϰ^– 1 ∇ f  + ^→Af  ) ^→n = 0 .

Теория Гинзбурга – Ландау

В.Л. Гинзбург и Л.Д. Ландау применили теорию фазовых переходов второго рода к сверхпроводимости, согласно которой свободную энергию можно разложить вблизи точки перехода по степеням параметра порядка. В качестве такого параметра они использовали волновую функцию сверхпроводящих электронов ψ .  Ее нормируют на плотность куперовских пар n_s  = 2 | ψ | ²  .  По предположению плотность свободной энергии для сверхпроводника в магнитном поле определяется выражением:
(1)   G_s  = G_n  + a | ψ | ²  + b2  | ψ | ⁴  +  14m | – iℏ∇ψ – 2ec ^→Aψ  | ²  +  H² 8π – (^→H ⋅ ^→H₀ ) 4π  . 
Здесь ^→H₀  – внешнее магнитное поле, в котором находится сверхпроводник; ^→H = rot ^→A – микроскопическое поле в данной точке сверхпроводника; a – коэффициент, зависящий от температуры по закону a = α (T – T_C )  ;  α,  b,  m – некоторые константы, связанные со сверхпроводящими свойствами; G_n  – энергия Гиббса в нормальном состоянии; 2e – заряд куперовской пары; 2m – ее эффективная масса.
При заданном внешнем поле и токах сверхпроводящих электронов, минимумом обладает термодинамический потенциал с плотностью магнитной энергией H² 8π  .  Но если задать только внешнее магнитное поле H₀  ,  как в нашем случае, то минимален потенциал с H² 8π – (^→H ⋅ ^→H₀ ) 4π  . 

Интегрируя (1) по объему, получим полную свободную энергию Гиббса сверхпроводника в виде функционала, который называют функционалом Гинзбурга – Ландау:
(2)   G_s  = ∫ G_s  dV = 
 G_n  + ∫ { a | ψ | ²  + b2  | ψ | ⁴  +  14m | – iℏ∇ψ – 2ec ^→Aψ  | ²  +  H² 8π – (^→H ⋅ ^→H₀ ) 4π  }  dV . 

Варьируя в (2) волновую функцию ψ и потенциал ^→A ,  можно получить уравнения Гинзбурга – Ландау (см. задачу 3.1):
(3)   14m ( – iℏ∇ – 2ec ^→A  ) ² ψ +  aψ + bψ | ψ | ²  = 0 ;
(4)   rot rot ^→A =  – i 2πℏemc (ψ^* ∇ψ – ψ∇ψ^* )  –  8πe² mc²   | ψ | ^2 →A . 
Уравнение (4) представляет собой хорошо известное уравнение Максвелла
^→j_s  = c4π rot rot ^→A = c4π rot ^→H
с плотностью тока в магнитном поле
(5)   ^→j_s  = – i ℏe2m (ψ^* ∇ψ – ψ∇ψ^* )  –  2e² mc  | ψ | ^2 →A . 

Граничные условия зависят от рассматриваемой задачи.
На границе раздела, за которой сверхпроводящее состояние невозможно, граничное условие для волновой функции следующее:
(6)   ( iℏ∇ψ + 2ec ^→Aψ  ) ^→n = 0 ,
где ^→n – единичный вектор, нормальный к поверхности сверхпроводника. Микроскопический анализ показывает, что такие условия выполняются лишь для контакта сверхпроводник – диэлектрик. Для контакта сверхпроводник – нормальный металл более точные граничные условия имеют вид
(7)   ( – iℏ∇ – 2ec ^→A  ) ^→nψ = iμψ . 
Граничные условия для векторного потенциала ^→A заключаются в том, что вектор магнитного поля ^→H = rot ^→A непрерывен на границе раздела:
(8)   ^→H = ^→H₀  . 

Для бесконечно протяженных сверхпроводников, граничные условия получаются из свойств системы на бесконечном удалении от границы фазового перехода:
обращение волновой функции в нуль ψ = 0 в нормальной фазе
и обращение в нуль сверхпроводящего тока электронов ^→j_s  = 0 в сверхпроводящей.

При отсутствии магнитного поля для пространственно однородных задач уравнение (3) примет вид
aψ + bψ | ψ | ²  = 0 ,
откуда
(9)    | ψ | ²  = n_s 2 = – ab  . 
И мы получаем важное соотношение, позволяющее выразить равновесную концентрацию сверхпроводящих электронов через параметры a и b  : 
(10)   n_s  = – 2 ab  . 
Когда температура равна критической (T = T_c )  ,  плотность сверхпроводящих электронов равна нулю n_s  = 0 . Это означает, что a → 0 при T → T₀  .  Параметр a можно разложить в ряд по степеням T_c  – T .  Оставляя только линейный член, имеем:
(11)   a = α (T – T_c )  . 
Параметр b вблизи T_c  остается постоянным. Можно показать также, что a < 0,  b > 0 . Действительно, подставляя в плотность энергии Гиббса
G_s  = G_n  + a | ψ | ²  + b2  | ψ | ⁴ 
равновесное значение плотности куперовских пар  | ψ | ²  = – ab  ,  имеем:
(12)   G_s  = G_n  – 12 a² b  . 
Поскольку для перехода в сверхпроводящее состояние должно быть G_s  < G_n  ,  то заключаем, что b > 0 , а используя выражение (10), видим, что a < 0 , так как плотность сверхпроводящих электронов не отрицательна.

Теперь рассмотрим сверхпроводник, находящийся во внешнем магнитном поле ^→H₀  .  Слабое поле не проникает вглубь сверхпроводника, поэтому в нем ^→H = 0 , и плотность энергии определяется из (12). Будем увеличивать поле, пока оно не достигнет критического значения ^→H_c  ,  при котором произойдет переход в нормальное состояние. В нем ψ = 0,  ^→H₀  = ^→H_c ,  ^→H = ^→H_c  ,  и из (1) получаем:
G_s  = G_n  – H²_c 8π  . 
Сравнивая с (12), получаем важное равенство, связывающее критическое магнитное поле H_c  с параметрами a и b  : 
(13)   H²_c  = 4π a² b  . 

В слабом магнитном поле, полагаем в уравнении (3) ^→A = 0 . Тогда оно имеет решение (9):
ψ = √  | a | b    . 
Подставляя в (4), приходим к уравнению Лондонов:
rot rot ^→A = – 8πe² mc²   | ψ | ^2 →A ; 
rot rot ^→A = – 1λ^2  →A
с глубиной проникновения магнитного поля
(14)   λ = √ mc² b8πe²  | a |    = √ mc² 4πn_s e²     . 

Перейдем к безразмерной функции  f (^→r )  ,  выполняя линейную замену
(15)   ψ (^→r )  = √  | a | b     f (^→r )   : 
(3)   14m ( – iℏ∇ – 2ec ^→A  ) ² ψ +  aψ + bψ | ψ | ²  = 0 ;
14m ( – iℏ∇ – ℏ 2πeπℏc ^→A  ) ²  f  +  af  +  | a |   f   |  f  | ²  = 0 ;
(16)   ξ² ( – i∇ – 2πΦ₀  ^→A  ) ²  f  –   f  +  f  |  f  | ²  = 0 .
Здесь Φ₀  = πℏce  – квант потока.
Параметр
ξ = √ ℏ² 4m | a |    
имеет размерность длины и носит название длины когерентности. Он определяет характерные расстояния изменения волновой функции в отсутствии магнитного поля (тогда можно положить ^→A = 0).

С помощью λ и ξ вводят очень важную величину – параметр Гинзбурга – Ландау:
(17)   ϰ = λ / ξ . 

Зависимость параметров от температуры

Согласно феноменологической теории фазовых переходов второго рода, разработанной Л.Д. Ландау, параметры a и b можно разложить в ряд по степеням T – T_c  .  Отбрасывая не существенные члены, полагают, что параметр a линейно зависит от температуры, а параметр b является постоянной:
(18)   a = α (T – T_c )    при   T → T_c  , 
где α – константа.

Эту зависимость удобно представить так:
(19)   a = a₀ ( 1 – TT_c   )  , 
где a₀  – некоторый коэффициент, который, в общем случае, не равен параметру a при нулевой температуре.

Тогда, используя (19), получаем зависимости от температуры других параметров теории ГЛ при T → T₀   : 
a = a₀ ( 1 – TT_c   )  ; 
b = const ; 
ξ = √ ℏ² 4m | a |    = ξ₀ ( 1 – TT_c   ) ^{– 1 / 2}  ; 
λ = √ mc² b8πe²  | a |    = λ₀ ( 1 – TT_c   ) ^{– 1 / 2}  ; 
ϰ = const ; 
n_s  = – 2 ab = n_s0 ( 1 – TT_c   )  ; 
H_c  = √ 4π a² b   = H_c0 ( 1 – TT_c   )  . 
Здесь a₀ ,  ξ₀ ,  λ₀ ,  n_s0 ,  H_c0  – коэффициенты, которые в общем случае не равны значениям при T = 0 .

Чтобы иметь возможность определять значения параметров во всем интервале температур 0 < T ≤ T_c  ,  применяют следующие эмпирические зависимости:
(20)   H_c (T )  = H_c (0 ) [ 1 – ( TT_c   ) ²  ]  ; 
(21)   λ (T )  = λ (0 ) [ 1 – ( TT_c   ) ⁴  ] ^{– 1 / 2}  . 

Величины T_c  и H_c (0 )  для некоторых металлов приведены в таблице 1.1; величины λ (0 )  – в приводимой ниже таблице 3.1.

Безразмерные уравнения ГЛ

В уравнения Гинзбурга – Ландау входит довольно много постоянных. Однако их число можно сократить, если сделать некоторые подстановки.

Для начала введем безразмерную волновую функцию  f   : 
ψ (^→r )  = √  | a | b     f (^→r )  . 
Тогда уравнение (3), как показано выше, примет вид
(16)   ξ² ( – i∇ – 2πΦ₀  ^→A  ) ²  f  –   f  +  f  |  f  | ²  = 0 .
Уравнение (4), граничные условия (6) и плотность тока (5) преобразуются так.
(4)   rot rot ^→A =  – i 2πℏemc (ψ^* ∇ψ – ψ∇ψ^* )  –  8πe² mc²   | ψ | ^2 →A ; 
rot rot ^→A =  – i 8πe²  | a |  ⋅ πℏcmc² b ⋅ 4πe ( f ^* ∇ f  –  f ∇ f ^* )  –  8πe²  | a | mc² b  |  f  | ^2 →A ; 
rot rot ^→A =  – i Φ₀ 4πλ²  ( f ^* ∇ f  –  f ∇ f ^* )  –  1λ²   |  f  | ^2 →A ; 
(22)   λ² rot rot ^→A =  – i Φ₀ 4π ( f ^* ∇ f  –  f ∇ f ^* )  –  |  f  | ^2 →A . 
(6) ( iℏ∇ f  + 2ec ^→Af  ) ^→n = 0 ;
( i∇ f  + 2πeπℏc ^→Af  ) ^→n = 0 ;
(23)   ( i∇ f  + 2πΦ₀  ^→A f  )  ⋅ ^→n = 0 .
(5)   ^→j_s  = – i ℏe2m (ψ^* ∇ψ – ψ∇ψ^* )  –  2e² mc  | ψ | ^2 →A ; 
^→j_s  =  – i 8πe²  | a | mc² b ⋅ c4π ⋅ πℏc4πe ( f ^* ∇ f  –   f ∇ f ^* )  – 8πe²  | a |  ⋅ cmc² b ⋅ 4π  |  f  | ^2 →A ; 
(24)   4πλ² c ^→j_s  =  – i Φ₀ 4π ( f ^* ∇ f  –  f ∇ f ^* )  –  |  f  | ^2 →A . 

За единицу длины возьмем λ ;  за единицу магнитного поля H_c  .  Перейдем к безразмерным величинам, которые будем обозначать подчеркиванием символов. Делаем подстановки:
^→r = λ^→r,  ^→H = H_c ^→H,  ^→A = λH_c ^→A . 
Преобразуем (16), (22), (23) и (24).
(16)   ξ² ( – i∇ – 2πΦ₀  ^→A  ) ²  f  –   f  +  f  |  f  | ²  = 0 ;
( – i ξλ ∇ – 2πξλH_c Φ₀  ^→A  ) ²  f  –   f  +  f  |  f  | ²  = 0 ;
(25)   ( – iϰ^– 1 ∇ – 1√ 2   ^→A  ) ²  f  –   f  +  f  |  f  | ²  = 0 .
(22)   λ² rot rot ^→A =  – i Φ₀ 4π ( f ^* ∇ f  –  f ∇ f ^* )  –  |  f  | ^2 →A ; 
λ² λH_c λ²  rot rot ^→A =  – i Φ₀ ξ2 ⋅ 2πλξ ( f ^* ∇ f  –  f ∇ f ^* )  –  λH_c  |  f  | ^2 →A ; 
λH_c rot rot ^→A =  – i √ 2  2 H_c ξ ( f ^* ∇ f  –  f ∇ f ^* )  –  λH_c  |  f  | ^2 →A ; 
(26)   rot rot ^→A =  – i √ 2  2 ϰ^– 1 ( f ^* ∇ f  –  f ∇ f ^* )  –   |  f  | ^2 →A ; 
(23)   ( i∇ f  + 2πΦ₀  ^→A f  )  ⋅ ^→n = 0 ;
( iξλ ∇ f  + 2πΦ₀  ξλH_c ^→Af  ) ^→n = 0 ;
(27)   ( iϰ^– 1 ∇ f  + 1√ 2   ^→Af  ) ^→n = 0 .

Задачи с решениями

Задача 3.1. Вывод уравнения ГЛ

Получить уравнение (3) с граничными условиями, варьируя комплексно-сопряженную волновую функцию ψ^*  в выражении для свободной энергии Гиббса.

Решение

Свободная энергия определяется функционалом:
(2)   G_s  = ∫ G_s  dV = G_n  +  a ∫ ψψ^*  dV + b2 ∫ ψ² (ψ^* ) ²  dV + 
 14m ∫ ( – iℏ∇ψ – 2ec ^→Aψ  )  ⋅  ( iℏ∇ψ^*  – 2ec ^→Aψ^*  )  dV + 
 ∫ (rot A ) ² 8π  dV –  14π ∫ (^→H₀  ⋅ rot ^→A )  dV . 
В равновесном состоянии это выражение должно иметь минимальное значение. Заменим ψ^* (^→r )  на ψ^* (^→r )  + δψ^* (^→r )  ,  где δψ^* (^→r )  – достаточно малая произвольная функция. В экстремуме выражение для свободной энергии, при такой замене, не должно содержать членов, линейных по δψ^* (^→r )  .  Найдем приращение функции G_s  . 
ΔG_s  = G_n  + a ∫ ψ (ψ^*  + δψ^* )  dV +  b2 ∫ ψ² (ψ^*  + δψ^* ) ²  dV + 
 14m ∫ ( – iℏ∇ψ – 2ec ^→Aψ  )  ⋅  (iℏ∇(ψ^*  + δψ^* )  –  2ec ^→A (ψ^*  + δψ^* ) )  dV + 
 ∫ (rot A ) ² 8π  dV –  14π ∫ (^→H₀  ⋅ rot ^→A )  dV – 
 G_n  – a ∫ ψψ^*  dV –  b2 ∫ ψ² (ψ^* ) ²  dV – 
 14m ∫ ( – iℏ∇ψ – 2ec ^→Aψ  )  ⋅  ( iℏ∇ψ^*  – 2ec ^→Aψ^*  )  dV – 
 ∫ (rot A ) ² 8π  dV +  14π ∫ (^→H₀  ⋅ rot ^→A )  dV . 
Отсюда, опуская члены квадратичные по δψ^*  ,  имеем:
ΔG_s  = a ∫ ψ δψ^*  dV +  b ∫ ψ² ψ^* δψ^*  dV + 
 iℏ4m ∫ ( – iℏ∇ψ – 2ec ^→Aψ  )  ⋅  (∇δψ^* )  dV –  14m ∫ ( – iℏ∇ψ – 2ec ^→Aψ  )  ⋅  2ec ^→Aδψ^*  dV = 0 .
Третье слагаемое интегрируем по частям:
∫ ( – iℏ∇ψ – 2ec ^→Aψ  ) (∇δψ^* )  dV = 
 ∫  ÷ [ ( – iℏ∇ψ – 2ec ^→Aψ  ) δψ^*  ]  dV – ∫ [ ∇( – iℏ∇ψ – 2ec ^→Aψ  )  ] δψ^*  dV . 
Преобразуем объемный интеграл в первом слагаемом в поверхностный. Согласно теореме Гаусса, получим:
ΔG_s  = a ∫ ψ δψ^*  dV +  b ∫ ψ² ψ^* δψ^*  dV + 
 iℏ4m ∫ ( – iℏ∇ψ – 2ec ^→Aψ  ) _n  ⋅  δψ^*  dS_n  +  14m ∫ [ – iℏ∇( – iℏ∇ψ – 2ec ^→Aψ  )  ]  ⋅  δψ^*  dV – 
 14m ∫ 2ec ^→A ( – iℏ∇ψ – 2ec ^→Aψ  )  ⋅  δψ^*  dV = 
 ∫ { 14m ( iℏ∇ψ + 2ec ^→Aψ  ) ²  +  aψ + bψ | ψ | ²  } δψ^*  dV + 
 iℏ4m ∫ ( – iℏ∇ψ – 2ec ^→Aψ  ) _n  ⋅  δψ^*  dS_n  = 0 .
Поскольку δψ^*  произвольно, то должны выполняться равенства:
14m ( iℏ∇ψ + 2ec ^→Aψ  ) ²  +  aψ + bψ | ψ | ²  = 0 ;
( iℏ∇ψ + 2ec ^→Aψ  ) _n  = 0 .

Задача 3.2. Калибровочная инвариантность

Показать, что при калибровочном преобразовании ^→A = ^→A^′ + ∇φ волновая функция умножается на фазовый множитель
ψ = ψ^′ exp ( i 2eℏc  φ  )  . 

Решение

Так как уравнения ГЛ получаются варьированием интеграла (2), то достаточно показать инвариантность этого выражения относительно указанной замены. Для первого и второго слагаемого это очевидно, поскольку
 | ψ | ²  = ψψ^*  = ψ^′e^{i 2eℏc  φ}  ψ^′ *e^{– i 2eℏc  φ}  =  ψ^′ψ^′ * =  | ψ^′ | ²  . 
Для четвертого и пятого слагаемых это также легко видеть
^→H = rot ^→A = rot (^→A^′ + ∇φ )  =  rot ^→A^′ + rot ∇φ = rot ^→A^′ + 0 = ^→H . 
Для третьего члена
∇ψ = ∇( ψ^′e^{i 2eℏc  φ}  )  =  (∇ψ^′ ) e^{i 2eℏc  φ}  + i 2eℏc (∇φ ) ψ^′e^{i 2eℏc  φ}  =  ( ∇ψ^′ + i 2eℏc (∇φ ) ψ^′  ) e^{i 2eℏc  φ}  . 
Далее
| – iℏ∇ψ – 2ec ^→Aψ  | ²  = 
 | – iℏ( ( ∇ψ^′ + i 2eℏc (∇φ ) ψ^′  ) e^{i 2eℏc  φ}  )   – 2ec (^→A^′ + ∇φ ) ψ^′e^{i 2eℏc  φ}  | ²  = 
 | ( – iℏ∇ψ^′ + 2ec (∇φ ) ψ^′  )  –  2ec (^→A^′ + ∇φ ) ψ^′  | ²  =  | – iℏ∇ψ^′ – 2ec ^→A^′  | ²  . 
Инвариантность доказана.

Задача 3.3

Свинцовый цилиндр находится при температуре 4,2 К в слабом однородном магнитном поле, параллельном его оси. Поле на поверхности цилиндра H₀  = 300 э. Найти плотность W магнитной энергии в свинце на расстоянии x = 300 Å от поверхности цилиндра (диаметр цилиндра много больше глубины проникновения магнитного поля).

Решение

По формуле (20), описывающей зависимость критического магнитного поля от температуры, используя значения T_c  и H_c (0 ) , находим величину критического магнитного поля при заданной температуре:
H_c (T )  = H_c (0 ) [ 1 – ( TT_c   ) ²  ]  = 528 э.
Считаем заданное поле H₀  = 300 э слабым. Тогда его влиянием на волновую функцию можно пренебречь, полагая ее значение постоянной величиной. Для безразмерной волновой функции  f  = 1 . Тогда второе уравнение ГЛ (22) приводит ко второму уравнению Лондонов:
H – λ² d² Hdx²  = 0 .
То есть величина магнитного поля зависит от расстояния x до поверхности сверхпроводника по экспоненциальному закону:
H (x )  = H₀ e^{– x / λ}  . 

Плотность магнитной энергии
W = H²  / 8π = H²₀ e^{– 2xλ (T )} / 8π . 
Зависимость глубины проникновения λ от температуры T определяется формулой (21). Значение λ (0 )  берем из таблицы 3.1.
λ (4,2 )  = 415 Å
Для плотности энергии получаем
W = 844 эрг/см³.

Задача 3.4

Критическая температура свинца равна 7,18 К. Во сколько раз глубина проникновения магнитного поля λ при температуре T = 7,10 К больше, чем глубина проникновения при T = 4,20 К? Оценить плотность сверхпроводящих электронов при температуре T = 7,10 К.

Решение

Во всем диапазоне температур λ (T )  хорошо аппроксимируется формулой (21), откуда получим
λ (7,10 ) λ (4,20 )  = 4,49 .

Используя результаты теории ГЛ, получим плотность сверхпроводящих электронов при температуре 7,10 К:
n_s  = 2  | a | b  ; 
λ²  = mc² b8πe²  | a |   ; 
n_s  = 2 mc² 8πe²  1λ²  =  mc² 4πe² λ² (0 )  √ 1 – ( TT₀   ) ⁴   =  8,06 ⋅ 10²⁰  см^-3.

Использованная литература:
О.Г. Одинцов, Е.А. Пушкарев, Методические указания к решению задач по физике сверхпроводников, Харьков, ХГУ, 1989.
Е.М. Лифшиц, Л.П. Питаевский, Статистическая физика. Часть 2. Теория конденсированного состояния, Москва, Физматлит, 2002.

Авторы: Олег Одинцов, Евгений Пушкарев.     Опубликовано: 12-07-2023