Математический анализ 1 курс
Описания и картинки страниц раздела “Математический анализ” сайта 1cov-edu.ru.
Предел последовательности – основные теоремы и свойства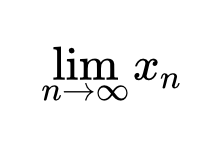
Приводятся формулировки основных теорем и свойств числовых последовательностей, имеющих предел. Содержится определение последовательности и ее предела. Рассмотрены арифметические действия с последовательностями, свойства, связанные с неравенствами, критерии сходимости, свойства бесконечно малых и бесконечно больших последовательностей. Предел функции – определения, теоремы и свойства
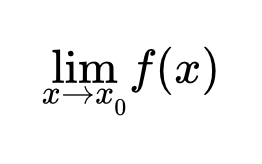Приводятся формулировки основных теорем и свойств предела функции. Даны определения конечных и бесконечных пределов в конечных точках и на бесконечности (двусторонних и односторонних) по Коши и Гейне. Рассмотрены арифметические свойства; теоремы, связанные с неравенствами; критерий сходимости Коши; предел сложной функции; свойства бесконечно малых, бесконечно больших и монотонных функций. Дано определение функции. Непрерывность функций – теоремы и свойства
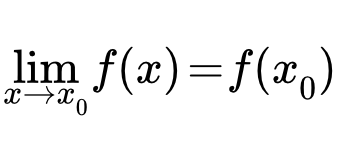Приводятся определения и формулировки основных теорем и свойств непрерывной функции одной переменной. Рассмотрены свойства непрерывной функции в точке, на отрезке, предел и непрерывность сложной функции, классификация точек разрыва. Даны определения и теоремы, связанные с обратной функцией. Изложены свойства элементарных функций. Методы вычисления пределов функций и раскрытия неопределенностей
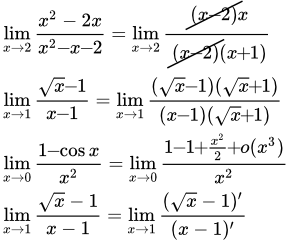Изложены приемы и методы решения задач на вычисление пределов и раскрытие неопределенностей. Рассмотрены следующие вопросы: пределы с непрерывными и сложными функциями; известные пределы; сведение неопределенности одного вида к другому; раскрытие неопределенностей с дробями из многочленов и корней; сравнение функций и решение разложением в степенной ряд; правило Лопиталя. Производная функции в точке – определения, теоремы и свойства
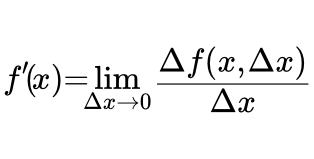Определения, теоремы и свойства производной и дифференциала функции одной переменной в точке. Методы вычислений и формулы производных элементарных функций. Производные и дифференциалы высших порядков. Правила дифференцирования - основные формулы вычисления производных
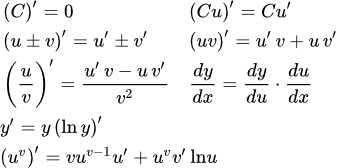В кратком виде даны правила дифференцирования (формулы вычисления производных). Ссылки на страницы с подробным описанием выбранного правила. Производные основных элементарных функций и их вывод
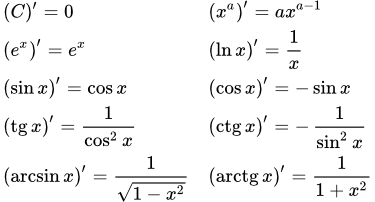Представлены производные основных элементарных функций и ссылки на страницы с их выводом. Даны формулы производных высших порядков. Производная функции на интервале
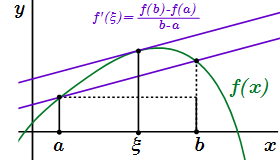Приводятся формулировки свойств и теорем, применяемых для исследования поведения функции на интервале с помощью производных. Методы вычисления неопределенных интегралов
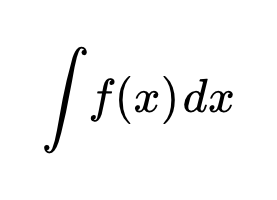Представлен обзор методов вычисления неопределенных интегралов. Рассмотрены основные методы интегрирования, которые включают в себя интегрирование суммы и разности, вынесение постоянной за знак интеграла, замену переменной, интегрирование по частям. Также рассмотрены специальные методы и приемы интегрирования дробей, корней, тригонометрических и показательных функций.
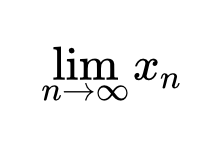Приводятся формулировки основных теорем и свойств числовых последовательностей, имеющих предел. Содержится определение последовательности и ее предела. Рассмотрены арифметические действия с последовательностями, свойства, связанные с неравенствами, критерии сходимости, свойства бесконечно малых и бесконечно больших последовательностей. Предел функции – определения, теоремы и свойства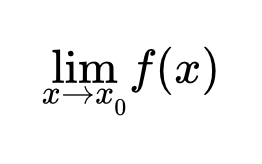Приводятся формулировки основных теорем и свойств предела функции. Даны определения конечных и бесконечных пределов в конечных точках и на бесконечности (двусторонних и односторонних) по Коши и Гейне. Рассмотрены арифметические свойства; теоремы, связанные с неравенствами; критерий сходимости Коши; предел сложной функции; свойства бесконечно малых, бесконечно больших и монотонных функций. Дано определение функции. Непрерывность функций – теоремы и свойства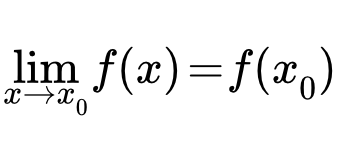Приводятся определения и формулировки основных теорем и свойств непрерывной функции одной переменной. Рассмотрены свойства непрерывной функции в точке, на отрезке, предел и непрерывность сложной функции, классификация точек разрыва. Даны определения и теоремы, связанные с обратной функцией. Изложены свойства элементарных функций. Методы вычисления пределов функций и раскрытия неопределенностей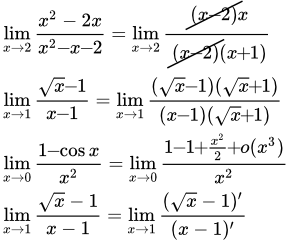Изложены приемы и методы решения задач на вычисление пределов и раскрытие неопределенностей. Рассмотрены следующие вопросы: пределы с непрерывными и сложными функциями; известные пределы; сведение неопределенности одного вида к другому; раскрытие неопределенностей с дробями из многочленов и корней; сравнение функций и решение разложением в степенной ряд; правило Лопиталя. Производная функции в точке – определения, теоремы и свойства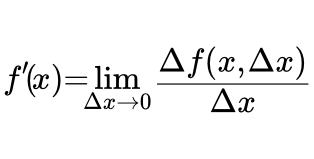Определения, теоремы и свойства производной и дифференциала функции одной переменной в точке. Методы вычислений и формулы производных элементарных функций. Производные и дифференциалы высших порядков. Правила дифференцирования - основные формулы вычисления производных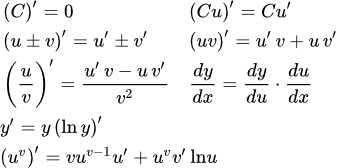В кратком виде даны правила дифференцирования (формулы вычисления производных). Ссылки на страницы с подробным описанием выбранного правила. Производные основных элементарных функций и их вывод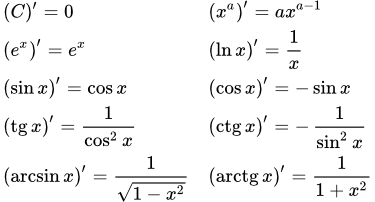Представлены производные основных элементарных функций и ссылки на страницы с их выводом. Даны формулы производных высших порядков. Производная функции на интервалеПриводятся формулировки свойств и теорем, применяемых для исследования поведения функции на интервале с помощью производных. Методы вычисления неопределенных интеграловПредставлен обзор методов вычисления неопределенных интегралов. Рассмотрены основные методы интегрирования, которые включают в себя интегрирование суммы и разности, вынесение постоянной за знак интеграла, замену переменной, интегрирование по частям. Также рассмотрены специальные методы и приемы интегрирования дробей, корней, тригонометрических и показательных функций.