Предел функции – определения, теоремы и свойства

Приводятся формулировки основных теорем и свойств предела функции. Даны определения конечных и бесконечных пределов в конечных точках и на бесконечности (двусторонних и односторонних) по Коши и Гейне. Рассмотрены арифметические свойства; теоремы, связанные с неравенствами; критерий сходимости Коши; предел сложной функции; свойства бесконечно малых, бесконечно больших и монотонных функций. Дано определение функции.

Содержание

См. также:

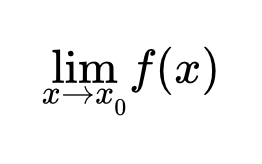
Определение предела функции

Первое определение предела функции по Гейне

Предел функции (по Гейне): при ее аргументе x, стремящемся к x₀ – это такое конечное число или бесконечно удаленная точка a, для которой выполняются следующие условия:
1) существует такая проколотая окрестность точки x₀, на которой функция f(x) определена;
2) для любой последовательности , сходящейся к :
,
элементы которой принадлежат окрестности , последовательность сходится к a:
.
Предел функции обозначают так:
.
Или при .
Здесь a и x₀ могут быть как конечными числами, так и бесконечно удаленными точками: .
Для бесконечно удаленных точек приняты следующие обозначения:
.
Проколотая окрестность конечной точки может быть как двусторонней, так и односторонней. В последнем случае, для левой окрестности пишут:
.
Для правой окрестности:
.

С помощью логических символов существования и всеобщности это определение можно записать следующим образом:

.

Второе определение по Коши

Предел функции (по Коши): при ее аргументе x, стремящемся к x₀ – это такое конечное число или бесконечно удаленная точка a, для которой выполняются следующие условия:
1) существует такая проколотая окрестность точки x₀, на которой функция f(x) определена;
2) для любой окрестности точки a, принадлежащей , существует такая проколотая окрестность точки x₀, на которой значения функции принадлежат выбранной окрестности точки a:
при .

Здесь a и x₀ также могут быть как конечными числами, так и бесконечно удаленными точками. С помощью логических символов существования и всеобщности это определение можно записать следующим образом:
.

Если в качестве множества взять левую или правую окрестность конечной точки, то получим определение предела по Коши слева или справа.

Теорема
Определения предела функции по Коши и по Гейне эквивалентны.
Доказательство

Применяемые окрестности точек

В приведенном выше определении применяются произвольные окрестности точек. Например, проколотой окрестностью конечной точки является множество , где – два положительных числа, которые определяют размер окрестности. Более подробно, см. «Окрестность точки».

Тогда, фактически, определение по Коши означает следующее.
Для любых положительных чисел , существуют числа , так что для всех x, принадлежащих проколотой окрестности точки : , значения функции принадлежат окрестности точки a: ,
где , .

С таким определением не совсем удобно работать, поскольку окрестности определяются с помощью четырех чисел . Но его можно упростить, если ввести окрестности с равноудаленными концами. То есть можно положить , . Тогда мы получим определение, которое проще использовать при доказательстве теорем. При этом оно является эквивалентным определению, в котором используются произвольные окрестности. Доказательство этого факта приводится в разделе «Эквивалентность определений предела функции по Коши».

Тогда можно дать единое определение предела функции в конечных и бесконечно удаленных точках:
.
Здесь для конечных точек
; ;
.
Любые окрестности бесконечно удаленных точек являются проколотыми:
; ; .

Далее мы приводим формулировки определений предела функции по Коши для разных случаев, используя определения окрестностей с равноудаленными концами.

Конечные пределы функции в конечных точках

Число a называется пределом функции f(x) в точке x₀,: если
1) функция определена на некоторой проколотой окрестности конечной точки ;
2) для любого существует такое , зависящее от , что для всех x, для которых , выполняется неравенство
.

С помощью логических символов существования и всеобщности определение предела функции можно записать следующим образом:
.

Односторонние пределы.
Левый предел в точке (левосторонний предел):
.
Правый предел в точке (правосторонний предел):
.
Пределы слева и справа часто обозначают так:
; .

Конечные пределы функции в бесконечно удаленных точках

Аналогичным образом определяются пределы в бесконечно удаленных точках.
.
.
.

Бесконечные пределы функции

Также можно ввести определения бесконечных пределов определенных знаков, равных и :
.
.

См. Бесконечный предел функции в конечной точке
Бесконечный предел функции на бесконечности

Свойства и теоремы предела функции

Далее мы считаем, что рассматриваемые функции определены в соответствующей проколотой окрестности точки , которая является конечным числом или одним из символов: . Также может быть точкой одностороннего предела, то есть иметь вид или . Окрестность является двусторонней для двустороннего предела и односторонней для одностороннего.

Основные свойства

Если значения функции f(x) изменить (или сделать неопределенными) в конечном числе точек x₁, x₂, x₃, ... x_n, то это изменение никак не повлияет на существование и величину предела функции в произвольной точке x₀.

Если существует конечный предел , то существует такая проколотая окрестность точки x₀, на которой функция f(x) ограничена:
.

Пусть функция имеет в точке x₀ конечный предел, отличный от нуля:
.
Тогда, для любого числа c из интервала , существует такая проколотая окрестность точки x₀, что для ,
, если ;
, если .

Если, на некоторой проколотой окрестности точки , – постоянная, то .

Функция имеет предел в точке тогда и только тогда, когда она имеет в этой точке равные односторонние пределы.

Если существуют конечные пределы и и на некоторой проколотой окрестности точки x₀
,
то .

Если , и на некоторой окрестности точки
,
то .
В частности, если на некоторой окрестности точки
,
то если , то и ;
если , то и .

Если на некоторой проколотой окрестности точки x₀:
,
и существуют конечные (или бесконечные определенного знака) равные пределы:
, то
.
См. Теорема о пределе промежуточной функции

Арифметические свойства предела функции

Пусть функции и определены в некоторой проколотой окрестности точки . И пусть существуют конечные пределы:
и .
И пусть C – постоянная, то есть заданное число. Тогда
;
;
;
, если .

Если , то .

Критерий Коши существования предела функции

Теорема
Для того, чтобы функция , определенная на некоторой проколотой окрестности конечной или бесконечно удаленной точки x₀, имела в этой точке конечный предел, необходимо и достаточно, чтобы для любого ε > 0 существовала такая проколотая окрестность точки x₀, что для любых точек и из этой окрестности, выполнялось неравенство:
.

Предел сложной функции

Теорема о пределе сложной функции
Пусть функции и имеют пределы:
;
.
И пусть существует такая проколотая окрестность точки , на которой
.
Тогда существует предел сложной функции , и он равен :
.
Здесь – конечные или бесконечно удаленные точки: . Окрестности и соответствующие им пределы могут быть как двусторонние, так и односторонние.
Доказательство

Теорема о пределе сложной функции применяется в том случае, когда функция не определена в точке или имеет значение, отличное от предельного . Для применения этой теоремы, должна существовать проколотая окрестность точки , на которой множество значений функции не содержит точку :
.

Теорема о пределе функции от монотонной функции
Пусть функции и имеют пределы:
;
.
И пусть существует такая проколотая окрестность точки , на которой функция строго монотонна. Причем монотонность слева и справа от может иметь разные знаки.
Тогда существует предел сложной функции , и он равен :
.
Здесь – конечные или бесконечно удаленные точки: . Окрестности и соответствующие им пределы могут быть как двусторонние, так и односторонние.
Доказательство

Предел сложной непрерывной функции

Если функция непрерывна в точке , то знак предела можно применять к аргументу непрерывной функции:
.
Далее приводится теорема, соответствующая этому случаю.

Теорема о пределе непрерывной функции от функции
Пусть существует предел функции t = g(x) при x → x₀, и он равен t₀:
.
Здесь точка x₀ может быть конечной или бесконечно удаленной: .
И пусть функция f(t) непрерывна в точке t₀.
Тогда существует предел сложной функции f(g(x)), и он равен f(t₀):
.

Бесконечно малые и бесконечно большие функции

Бесконечно малые функции

Бесконечно малая функция: при – это такая функция , предел которой при равен нулю:
.

Сумма, разность и произведение конечного числа бесконечно малых функций при является бесконечно малой функцией при .

Произведение функции, ограниченной на некоторой проколотой окрестности точки , на бесконечно малую при является бесконечно малой функцией при .

Для того, чтобы функция имела конечный предел , необходимо и достаточно, чтобы
,
где – бесконечно малая функция при .

Доказательства свойств изложены в разделе
«Свойства бесконечно малых функций».

Бесконечно большие функции

Бесконечно большая функция: при – это такая функция , предел которой при равен бесконечности:
.

Свойства бесконечно больших функций

Сумма или разность ограниченной функции, на некоторой проколотой окрестности точки , и бесконечно большой функции при является бесконечно большой функцией при .

Если функция является бесконечно большой при , а функция – ограничена, на некоторой проколотой окрестности точки , то
.

Если функция , на некоторой проколотой окрестности точки , удовлетворяет неравенству:
,
а функция является бесконечно малой при :
, и (на некоторой проколотой окрестности точки ), то
.

Cм. также: Свойства неравенств с бесконечно большими функциями ⇑.

Доказательства свойств изложены в разделе
«Свойства бесконечно больших функций».

Связь между бесконечно большими и бесконечно малыми функциями

Из двух предыдущих свойств вытекает связь между бесконечно большими и бесконечно малыми функциями.

Если функция являются бесконечно большой при , то функция является бесконечно малой при .

Если функция являются бесконечно малой при , и , то функция является бесконечно большой при .

Связь между бесконечно малой и бесконечно большой функцией можно выразить символическим образом:
, .

Если бесконечно малая функция имеет определенный знак при , то есть положительна (или отрицательна) на некоторой проколотой окрестности точки , то этот факт можно выразить так:
.
Точно также если бесконечно большая функция имеет определенный знак при , то пишут:
.

Тогда символическую связь между бесконечно малыми и бесконечно большими функциями можно дополнить следующими соотношениями:
, ,
, .

Дополнительные формулы, связывающие символы бесконечности, можно найти на странице
«Бесконечно удаленные точки и их свойства».

Пределы монотонных функций

Строго возрастающая функция: Функция , определенная на некотором множестве действительных чисел X называется строго возрастающей, если для всех таких что выполняется неравенство:
.
Строго убывающая функция: Функция называется строго убывающей, если для всех таких что выполняется неравенство:
.
Неубывающая функция: Функция называется неубывающей, если для всех ; :
.
Невозрастающая функция: Функция называется невозрастающей, если для всех ; :
.
Монотонная функция: Функция называется монотонной, если она неубывающая или невозрастающая.

Отсюда следует, что строго возрастающая функция также является неубывающей. Строго убывающая функция также является невозрастающей.

Теорема
Пусть функция не убывает на интервале , где .
Если она ограничена сверху числом M: , то существует конечный предел . Если не ограничена сверху, то .
Если ограничена снизу числом m: , то существует конечный предел . Если не ограничена снизу, то .

Если точки a и b являются бесконечно удаленными, то в выражениях под знаками пределов подразумевается, что .
Эту теорему можно сформулировать более компактно.

Пусть функция не убывает на интервале , где . Тогда существуют односторонние пределы в точках a и b:
;
.

Аналогичная теорема для невозрастающей функции.

Пусть функция не возрастает на интервале , где . Тогда существуют односторонние пределы:
;
.

Определение функции, верхней и нижней грани

Функцией: y = f(x) называется закон (правило), согласно которому, каждому элементу x множества X ставится в соответствие один и только один элемент y множества Y.

Элемент x ∈ X называют аргументом функции или независимой переменной.
Элемент y ∈ Y называют значением функции или зависимой переменной.

Множество X называется областью определения функции.
Множество элементов y ∈ Y, которые имеют прообразы в множестве X, называется областью или множеством значений функции.

Если это особо не оговорено, мы рассматриваем функции, области определения и множества значений которых принадлежат множеству действительных чисел.

Ограниченная функция: Действительная функция называется ограниченной сверху (снизу), если существует такое число M, что для всех выполняется неравенство:
.
Числовая функция называется ограниченной, если существует такое число M, что для всех :
.
Верхняя грань функции: Верхней гранью или точной верхней границей действительной функции называют наименьшее из чисел, ограничивающее область ее значений сверху. То есть это такое число s, для которого для всех и для любого , найдется такой аргумент , значение функции от которого превосходит s′: .
Верхняя грань функции может обозначаться так:
.
Нижняя грань функции: Нижней гранью или точной нижней границей действительной функции называют наибольшее из чисел, ограничивающее область ее значений снизу. То есть это такое число i, для которого для всех и для любого , найдется такой аргумент , значение функции от которого меньше чем i′: .
Нижняя грань функции может обозначаться так:
.

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов. Опубликовано: 04-04-2018 Изменено: 28-11-2021

См. также: