Непрерывность функций – теоремы и свойства

Приводятся определения и формулировки основных теорем и свойств непрерывной функции одной переменной. Рассмотрены свойства непрерывной функции в точке, на отрезке, предел и непрерывность сложной функции, классификация точек разрыва. Даны определения и теоремы, связанные с обратной функцией. Изложены свойства элементарных функций.

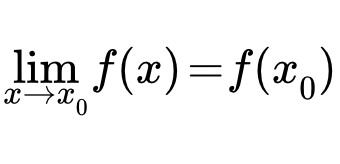
Определение

Непрерывная функция в точке

Функция f(x) называется непрерывной в точке x₀, если она определена на некоторой окрестности этой точки, если существует предел при x стремящемся к x₀, и если этот предел равен значению функции в x₀:
.

Используя определения предела функции по Коши и по Гейне, можно дать развернутые определения непрерывности функции в точке.

Можно сформулировать понятие непрерывности в терминах приращений. Для этого мы вводим новую переменную , которая называется приращением переменной x в точке . Тогда функция непрерывна в точке , если
.
Введем новую функцию:
.
Ее называют приращением функции в точке . Тогда функция непрерывна в точке , если
.

Непрерывность функции справа (слева)

Функция f(x) называется непрерывной справа (слева) в точке x₀, если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x₀ равен значению функции в x₀:
.

Более подробно, см. «Определение непрерывности функции в точке».

Свойства непрерывных в точке функций

Теорема об ограниченности непрерывной функции
Пусть функция f(x) непрерывна в точке x₀. Тогда существует такая окрестность U(x₀), на которой функция ограничена.

Теорема о сохранении знака непрерывной функции
Пусть функция непрерывна в точке . И пусть она имеет положительное (отрицательное) значение в этой точке:
.
Тогда существует такая окрестность точки , на которой функция имеет положительное (отрицательное) значение:
  при  .

Арифметические свойства непрерывных функций
Пусть функции   и   непрерывны в точке .
Тогда функции , и непрерывны в .
Если , то и функция непрерывна в точке .

Свойство непрерывности слева и справа
Функция непрерывна в точке тогда и только тогда, когда она непрерывна в справа и слева.

Доказательства свойств приводятся на странице «Свойства непрерывных в точке функций».

Непрерывность сложной функции

Теорема о непрерывности сложной функции
Пусть функция t = g(x)  непрерывна в точке x₀. И пусть функция f(t)  непрерывна в точке t₀ = g(x₀).
Тогда сложная функция  f(g(x)) непрерывна в точке x₀.
Доказательство

Предел сложной функции

Теорема о пределе непрерывной функции от функции
Пусть существует предел функции t = g(x) при x → x₀, и он равен t₀:
.
Здесь точка x₀ может быть конечной или бесконечно удаленной: .
И пусть функция f(t)  непрерывна в точке t₀.
Тогда существует предел сложной функции f(g(x)), и он равен f(t₀):
.
Доказательство

Теорема о пределе сложной функции
Пусть функции   и   имеют пределы:
;
.
И пусть существует такая проколотая окрестность точки , на которой
.
Тогда существует предел сложной функции , и он равен :
.
Здесь – конечные или бесконечно удаленные точки: . Окрестности и соответствующие им пределы могут быть как двусторонние, так и односторонние.
Доказательство

Определения точек разрыва

Точка разрыва функции

Пусть функция определена на некоторой проколотой окрестности точки . Точка называется точкой разрыва функции , если выполняется одно из двух условий:
1) не определена в ;
2) определена в , но не является непрерывной ⇑ в этой точке.

Точка разрыва первого рода

Точка называется точкой разрыва первого рода, если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.

Скачок функции

Скачком Δ функции в точке называется разность пределов справа и слева
.

Точка устранимого разрыва

Точка называется точкой устранимого разрыва, если существует предел
,
но функция в точке или не определена, или не равна предельному значению: .

Таким образом, точка устранимого разрыва – это точка разрыва 1-го рода, в которой скачек функции равен нулю.

Точка разрыва второго рода

Точка называется точкой разрыва второго рода, если она не является точкой разрыва 1-го рода. То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.

Подробнее, см. «Точки разрыва функции – определения, классификация и примеры».

Свойства функций, непрерывных на отрезке

Непрерывная функция на отрезке

Функция называется непрерывной на отрезке (при ), если она непрерывна во всех точках открытого интервала (при ) и непрерывна справа и слева ⇑ в точках a и b, соответственно.

Первая теорема Вейерштрасса об ограниченности непрерывной на отрезке функции
Если функция непрерывна на отрезке , то она ограничена на этом отрезке.

Достижимость максимума (минимума)

Функция достигает своего максимума (минимума) на множестве , если существует такой аргумент , для которого
для всех .

Достижимость верхней (нижней) грани

Функция достигает своей верхней (нижней) грани на множестве , если существует такой аргумент , для которого
.

Вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции
Непрерывная на отрезке функция достигает на нем своих верхней и нижней граней или, что тоже самое, достигает на отрезке своего максимума и минимума.

Теорема Больцано – Коши о промежуточном значении
Пусть функция непрерывна на отрезке . И пусть C есть произвольное число, находящееся между значениями функции на концах отрезка: и . Тогда существует точка , для которой
.

Следствие 1
Пусть функция непрерывна на отрезке . И пусть значения функции на концах отрезка имеют разные знаки: или . Тогда существует точка , значение функции в которой равно нулю:
.

Следствие 2
Пусть функция непрерывна на отрезке . И пусть . Тогда функция принимает на отрезке все значения из и только эти значения:
  при  .

Подробнее, см. «Свойства функций, непрерывных на отрезке».

Обратные функции

Обратная функция

Пусть функция имеет область определения X и множество значений Y. И пусть она обладает свойством:
для всех .
Тогда для любого элемента из множества Y можно поставить в соответствие только один элемент множества X, для которого . Такое соответствие определяет функцию, которая называется обратной функцией к . Обратная функция обозначается так:
.

Из определения следует, что
;
  для всех  ;
  для всех  .

Лемма о взаимной монотонности прямой и обратной функций
Если функция строго возрастает (убывает), то существует обратная функция , которая также строго возрастает (убывает).

Свойство о симметрии графиков прямой и обратной функций
Графики прямой и обратной функций симметричны относительно прямой .

Теорема о существовании и непрерывности обратной функции на отрезке
Пусть функция непрерывна и строго возрастает (строго убывает) на отрезке . Тогда на отрезке определена и непрерывна обратная функция , которая строго возрастает (строго убывает).
Для возрастающей функции .
Для убывающей: .

Теорема о существовании и непрерывности обратной функции на интервале
Пусть функция непрерывна и строго возрастает (строго убывает) на открытом конечном или бесконечном интервале . Тогда на интервале определена и непрерывна обратная функция , которая строго возрастает (строго убывает).
Для возрастающей функции .
Для убывающей: .

Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.

Подробнее, см. «Обратные функции – определение и свойства».

Свойства и непрерывность элементарных функций

Элементарные функции и обратные к ним непрерывны на своей области определения. Далее мы приводим формулировки соответствующих теорем и даем ссылки на их доказательства.

Показательная функция

Показательная функция

Показательная функция f(x) = a^x, с основанием a > 0 – это предел последовательности
,
где есть произвольная последовательность рациональных чисел, стремящаяся к x:
.

Подробнее, см. «Определение и доказательство свойств показательной функции».

Логарифм

Логарифмическая функция

Логарифмическая функция, или логарифм, y = log_a x, с основанием a – это функция, обратная к показательной функции с основанием a.

Подробнее, см. «Определение и доказательство свойств логарифма».

Экспонента и натуральный логарифм

В определениях показательной функции и логарифма фигурирует постоянная a, которая называется основанием степени или основанием логарифма. В математическом анализе, в подавляющем большинстве случаев, получаются более простые вычисления, если в качестве основания использовать число e:
.
Показательную функцию с основанием e называют экспонентой: , а логарифм по основанию e – натуральным логарифмом: .

Свойства экспоненты и натурального логарифма изложены на страницах
«Число e – его смысл и доказательство сходимости последовательности»;
«Экспонента, е в степени х»;
«Натуральный логарифм, функция ln x».

Степенная функция

Степенная функция

с показателем степени p – это функция  f(x) = x ^p, значение которой в точке x равно значению показательной функции с основанием x в точке p.
Кроме этого,  f(0) = 0 ^p = 0  при  p > 0.

Здесь мы рассмотрим свойства степенной функции y = x ^p при неотрицательных значениях аргумента . Для рациональных , при нечетных m, степенная функция определена и для отрицательных x. В этом случае, ее свойства можно получить, используя четность или нечетность.
Эти случаи подробно рассмотрены и проиллюстрированы на странице «Степенная функция, ее свойства и графики».

Подробнее, см. «Непрерывность и свойства степенной функции».

Тригонометрические функции

Теорема о непрерывности тригонометрических функций
Тригонометрические функции: синус (sin x), косинус (cos x), тангенс (tg x) и котангенс (ctg x), непрерывны на своих областях определения.

Теорема о непрерывности обратных тригонометрических функций
Обратные тригонометрические функции: арксинус (arcsin x), арккосинус (arccos x), арктангенс (arctg x) и арккотангенс (arcctg x), непрерывны на своих областях определения.

Подробнее, см. «Доказательство непрерывности тригонометрических функций».

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов.     Опубликовано: 15-08-2018   Изменено: 09-06-2020