Общее уравнение динамики. Пример решения задачи

Пример решения задачи с применением общего уравнения динамики (принцип Даламбера – Лагранжа) для системы с твердыми телами, грузами, шкивами и блоком, соединенных нитями.

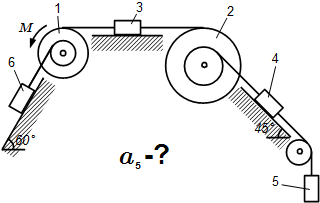
Условие задачи

Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3-6, прикрепленных к этим нитям, и невесомого блока. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом M = 10 Н·м, приложенной к шкиву 1. Радиусы ступеней шкива 1 равны: R₁ = 0,2 м, r₁ = 0,1 м, а шкива 2 – R₂ = 0,3 м, r₂ = 0,15 м; их радиусы инерции относительно осей вращения равны соответственно ρ₁ = 0,1 м и ρ₂ = 0,2 м.

Пренебрегая трением, определить ускорение груза 5. Веса шкивов и грузов заданы: P₁ = 40 Н, P₂ = 0, P₃ = 0, P₄ = 20 Н, P₅ = 30 Н, P₆ = 10 Н. Грузы, веса которых равны нулю, на чертеже не изображать.

Указание. При решении задачи использовать общее уравнение динамики (принцип Даламбера – Лагранжа).

Решение задачи

Дано: R₁ = 0,2 м, r₁ = 0,1 м, R₂ = 0,3 м, r₂ = 0,15 м, ρ₁ = 0,1 м, ρ₂ = 0,2 м. P₁ = 40 Н, P₂ = 0, P₃ = 0, P₄ = 20 Н, P₅ = 30 Н, P₆ = 10 Н, M = 10 Н·м.

Найти: a₅.

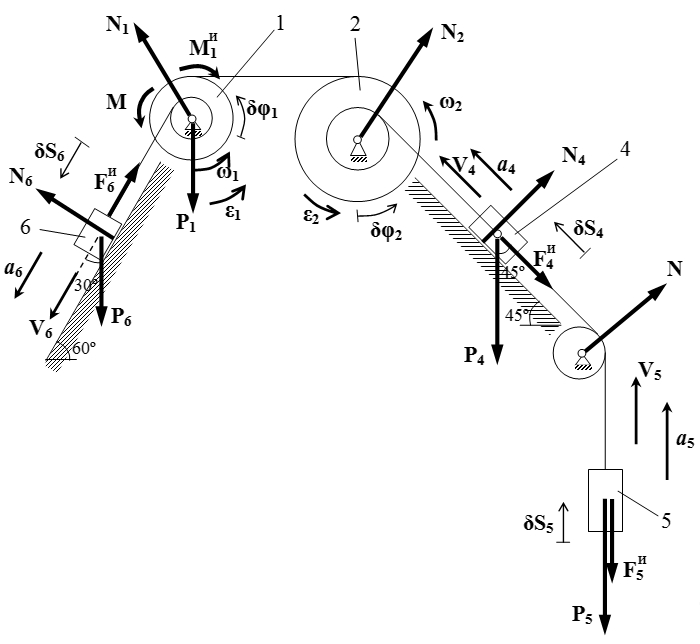
Установление кинематических соотношений

Установим кинематические соотношения. Пусть V₄, V₅, V₆, a₄, a₅, a₆, δS₄, δS₅, δS₆ – скорости, ускорения и малые перемещения грузов 4,5 и 6. Пусть ω₁, ω₂, ε₁, ε₂, δφ₁, δφ₂ – угловые скорости, угловые ускорения и малые углы поворота шкивов 1 и 2.

Скорость движения нити между телами 2, 4 и 5:
. Отсюда .
Скорость движения нити между шкивами 1 и 2:
. Отсюда
.
Скорость движения нити между телами 1 и 6:
.

Итак, мы нашли связь между скоростями тел.
;
;
.

Поскольку ускорения – это производные скоростей по времени, ,
то дифференцируя по времени предыдущие формулы, находим связь между ускорениями:
;
;
.

Поскольку скорости – это производные от перемещений по времени, то такая же связь есть между бесконечно малыми перемещениями.
;
;
.

Активные внешние силы

Рассмотрим внешние силы, действующие на систему.
Это силы тяжести тел P₁ = 40 Н, P₄ = 20 Н, P₅ = 30 Н и P₆ = 10 Н, направленные вниз;
заданная пара сил с моментом M = 10 Н·м;
силы давления осей N₁, N₂ и N шкивов 1, 2 и невесомого блока;
силы реакции N₄ и N₆, действующие на грузы со стороны поверхностей, перпендикулярные этим поверхностям.

Силы инерции

Мы будем решать эту задачу с помощью общего уравнения динамики, применяя принцип Даламбера - Лагранжа. Он заключается в том, что сначала мы вводим силы инерции. После введения сил инерции, задача динамики превращается в задачу статики. То есть нам нужно найти неизвестные силы инерции, чтобы система находилась в равновесии. Данную задачу статики мы решаем, применяя принцип Даламбера. То есть считаем, что система совершила малое перемещение. Тогда в равновесии, сумма работ всех сил, при таком перемещении, равна нулю.

Итак, на первом этапе мы вводим силы инерции. Для этого предполагаем, что система движется с некоторым, пока не определенным, ускорением. То есть шкивы 1 и 2 вращаются с угловыми ускорениями ε₁ и ε₂, соответственно; грузы 4,5 и 6 совершают поступательное движение с ускорениями a₄, a₅ и a₆, соответственно. Между этими ускорениями имеются связи, которые мы нашли ранее. То есть все эти ускорения можно выразить через одно ускорение a₅. Силы инерции определяются так, что они равны по модулю и противоположны по направлению тем силам (и моментам сил), которые, по законам динамики, создавали бы предполагаемые ускорения (при отсутствии других сил).

Определяем модули (абсолютные значения) сил и моментов инерции и выражаем их через a₅.
Пусть – массы тел;
– момент инерции шкива 1.
Момент сил инерции, действующий на шкив 1:
.
Силы инерции, действующие на грузы 4, 5 и 6:
;
;
.

Изображаем силы инерции на чертеже учитывая, что их направления противоположны ускорениям.

Применение общего уравнения динамики

Даем системе бесконечно малое перемещение. Пусть груз 5 переместился на малое расстояние δS₅. Тогда угол поворота δφ₁ шкива 1 и перемещения δS₄ и δS₆ грузов 4 и 6 определяются с помощью установленных ранее кинематических соотношений. Поскольку нити нерастяжимые, то они не совершают работу при таком перемещении. Это означает, что система имеет идеальные связи. Поэтому мы можем применить общее уравнение динамики:
,
согласно которому сумма работ всех активных сил и сил инерции, при таком перемещении, равна нулю.

Определение суммы работ внешних активных сил и сил инерции

Работа, которую совершает сила     при перемещении точки ее приложения на малое смещение     равна скалярному произведению векторов   , то есть произведению модулей векторов F и ds на косинус угла между ними.

Работа, произведенная моментом сил   , вычисляется аналогично:
.

Определяем работы всех активных сил и сил инерции. Поскольку центры осей шкивов 1, 2 и невесомого блока не совершают перемещений, то силы P₁, N₁, N₂ и N не совершают работу. Поскольку силы N₄ и N₆ перпендикулярны перемещениям грузов 4 и 6, то эти силы также не совершают работу.

Находим сумму работ остальных активных сил и сил инерции.

.
Подставляем выражения для сил инерции и применяем кинематические соотношения.

.
Сокращаем на δS₅ и преобразовываем.

.
Подставляем численные значения.

;
;
м/с².

Ответ

м/с².

Автор: Олег Одинцов.     Опубликовано: 02-08-2015