Решение задач на применение теоремы об изменении кинетического момента системы

Инструкция о порядке решения задач на применение теоремы об изменении кинетического момента системы. Рассмотрены примеры решения задач с краткими и подробными решениями.

Как решить задачу на применение теоремы моментов для системы, вращающейся вокруг оси

1. Выбрать инерциальную систему координат Oxyz, направив одну из осей, скажем Oz, вдоль оси вращения системы.
2. Изобразить на рисунке все внешние силы , действующие на элементы системы.
3. Найти сумму моментов внешних сил относительно оси вращения Oz.
4. Найти главный момент количества движения (кинетический момент) системы относительно оси Oz.
5. Применить теорему об изменении кинетического момента системы для компоненты z.
   Производная по времени от главного момента количества движения системы относительно оси равна сумме моментов всех внешних сил, действующих на систему, относительно этой оси.
   .
   
6. В результате мы получим одно уравнение, связывающие неизвестные величины. Если в задаче всего одна неизвестная величина (например, угловая скорость в заданный или произвольный момент времени), то это уравнение позволяет ее найти. Если неизвестных величин несколько, скажем n, то, для их определения, требуется составить еще n – 1 уравнений, применяя другие законы.

Задача 1. Определение угловой скорости вращающейся платформы с движущимся по ней грузом

Условие задачи

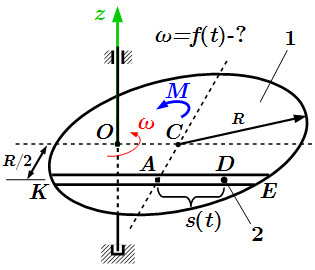
Однородная круглая радиуса R = 1,2 м горизонтальная платформа массой m₁ = 24 кг вращается с угловой скоростью ω₀ = 10 с^-1 вокруг вертикальной оси z, отстоящей от центра масс C платформы на расстоянии OC = b = R/2.

В момент времени t₀ = 0 с по желобу платформы, под действием внутренних сил, начинает двигаться груз D массой m₂ = 10 кг по закону , где s выражено в метрах, t – в секундах. Одновременно на платформу действует пара сил с моментом (в ньютон-метрах). Положительное направление M показано на рисунке. Форма желоба прямолинейная. На рисунке груз D показан в положении, при котором .

Определить зависимость угловой скорости платформы как функцию времени: .

Указания. Эта задача – на применение теоремы об изменении кинетического момента системы.

Краткое решение

Находим сумму моментов внешних сил относительно оси Oz:


.
Вычисляем кинетический момент системы относительно оси Oz.
(1.1)   .
Вычисляем кинетический момент плиты, считая ее твердым телом.
.
Применяем теорему Штейнера.
;
.
Вычисляем кинетический момент груза, считая его материальной точкой.
.

Применяем теорему о сложении скоростей при сложном движении точки.
;
;
;
;
.
Применяем теорему Вариньона.


;
;
.
Применяем теорему об изменении кинетического момента системы.
;
.
Интегрируем.
;
;
;
;
;
;
;
;
.

Подробное решение с объяснениями

Дано:   m₁=24 кг, m₂=10 кг, R = 1,2 м, OC = b = R/2, AC = R/2, (м), M = 2 + t² (Нм), t₀=0 с, ω₀=10 с^-1.
Найти: .
Решение.

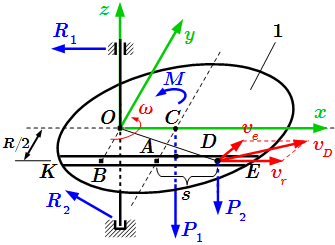
1. Выбираем инерциальную (неподвижную) систему отсчета . Ось Oz направим вдоль оси вращения; оси Ox и Oy – в плоскости платформы; ось Oy проходит через центр C платформы (см. рисунок).

2. Рассмотрим внешние силы , действующие на элементы системы. Это силы тяжести платформы и груза, направленные вниз; силы реакции вала ; заданная пара сил с моментом M.

3. Найдем сумму моментов внешних сил относительно оси Oz.
Силы тяжести направлены вниз, то есть они параллельны оси вращения. Поэтому их моменты равны нулю: .
Силы реакций проходят через ось вращения. Их моменты также равны нулю: .
В результате мы получаем, что сумма моментов внешних сил равна моменту заданной пары сил, направленному вдоль оси Oz:

;
(1.2)   .

4. Вычисляем главный момент (сумму моментов) количества движения системы относительно оси Oz. Он равен сумме моментов плиты и груза:
.

4.1. Вычисляем кинетический момент плиты, считая ее твердым телом.
.
Здесь – момент инерции плиты относительно оси Oz. Плита является сплошным однородным диском радиуса R. Из любого справочника можно найти момент инерции однородного диска относительно оси Cz, проходящей через его центр масс C, совпадающим с центром окружности:
.
В нашем случае, ось Oz параллельна оси Cz, проходящей через центр масс тела, и находится от нее на расстоянии . Применяем теорему Штейнера:
;
.
Кинетический момент плиты:
(1.3)   .

4.2. Вычисляем кинетический момент груза, считая его материальной точкой. Он вычисляется по тем же правилам, что и момент силы. Только вектор силы нужно заменить на вектор скорости, умноженный на массу точки (это произведение называется количеством движения, или импульсом точки).
(1.4)   .
Здесь – скорость груза в неподвижной системе координат.

Нам известна скорость груза относительно плиты. Кроме этого, плита вращается вокруг оси Oz. Рассмотрим движение груза как сложное, и применим теорему о сложении скоростей.
.
Здесь и – переносная и относительная скорость груза.

Подставляем в (1.4), и применяем свойство векторного произведения:
;
(1.5)   , где
.
Мы получили, что если скорость точки представить в виде геометрической суммы скоростей и , то ее кинетический момент равен сумме кинетических моментов от скоростей и . Этот результат аналогичен теореме Вариньона, применяемой в статике, согласно которой, если силу можно разложить на составляющие и : , то момент силы равен сумме моментов от и :
.
Уравнение (1.5) можно записать аналогичным образом:
.
Далее мы будем вычислять кинетические моменты от переносной и относительной скоростей по правилам вычисления момента силы, заменив ее на вектор скорости, умноженный на массу точки:
.

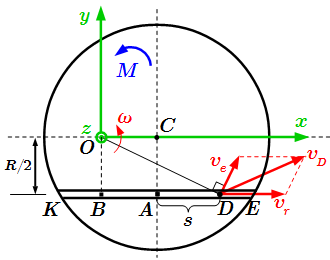
Найдем переносную скорость . Это скорость точки D плиты, в которой находится груз в рассматриваемый момент времени. Эта точка расположена на расстоянии от центра O, и вращается вокруг него с угловой скоростью ω. Поэтому
.
Вектор лежит в плоскости Oxy плиты, и направлен перпендикулярно OD. Поскольку , то OD является плечом вектора относительно центра O. Тогда
;
(1.6)   .
Из точки O опустим перпендикуляр на прямую KE. Получаем прямоугольный треугольник OBD, из которого имеем:

.
Подставляем в (1.6):
(1.7)   .

Найдем относительную скорость . Это скорость груза D относительно плиты. То есть это скорость, которую имел бы груз, если бы плита покоилась. По условию, груз движется по прямолинейному желобу KE. Известна зависимость расстояния до точки A от времени:
.
Тогда скорость , по абсолютной величине, равна производной s по времени t, и направлена вдоль желоба KE.
.
Здесь – единичный вектор, направленный от K к E.
Отрезок OB перпендикулярен направлению вектора скорости , причем точка B лежит на линии действия . Поэтому OB является плечом скорости . Тогда
(1.8)   .

Применяя формулы (1.1), (1.5), (1.3), (1.7) и (1.8), получаем выражение для кинетического момента системы относительно оси Oz:
(1.9)   .

5. Применяем теорему об изменении кинетического момента системы, подставляя (1.2).
;
.
Правая часть зависит только от времени t. Поэтому это уравнение можно проинтегрировать.
;
.
Здесь – постоянная интегрирования, которая определяется из начальных условий.

6. Подставляем (1.9):
.
Вычисляем производную и подставляем численные значения величин:
;
;
(1.10)   .
Определяем значение постоянной . По условию, в момент времени , плита вращалась с угловой скоростью с^-1. Подставляем :
;
.
Из (1.10) окончательно имеем:
;
.

Ответ

.
Здесь t выражено в секундах, ω – в с^-1.

Задача 2. Движение точки по канату, перекинутому через блок

Условие задачи

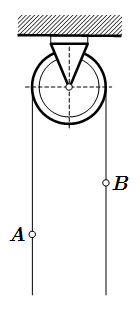
Через блок перекинут канат; за точку A каната ухватился человек, к точке B подвязан груз одинаковой массы с человеком. Что произойдет с грузом, если человек станет подниматься по канату со скоростью v относительно каната? Масса блока в четыре раза меньше массы человека, и равномерно распределена по его ободу.

Источник:
И. В. Мещерский, Сборник задач по теоретической механике, задача 37.51, стр. 290. Москва, «Наука», 1986.

Краткое решение

Вводим обозначения.
.
Находим сумму моментов внешних сил относительно оси Oz (перпендикулярна плоскости рисунка и направлена на нас):



.
Находим главный момент количества движения системы относительно оси Oz.

.
Применяем теорему о сложении скоростей при сложном движении точки.
.
Проектируем на ось , и выполняем преобразования.
;
.
Применяем теорему об изменении кинетического момента системы.
;
;
;
.
При ;
;
.

Подробное решение с объяснениями

Дано:   m_A = m_B = m, m₃=m/4, v, масса блока 3 равномерно распределена по его ободу.
Найти: v_B.
Решение.

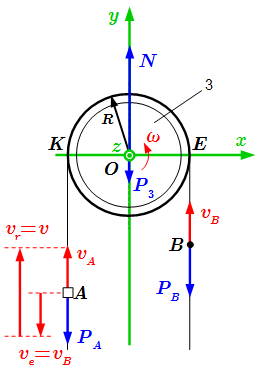
1. Выберем инерциальную систему координат Oxyz с началом в центре O блока 3. Ось z перпендикулярна плоскости рисунка, и направлена на нас.

2. Рассмотрим систему, состоящую из человека A, груза B и блока 3. Считаем, что человек и груз являются материальными точками. Рассмотрим внешние силы, действующие на систему. Это силы тяжести человека , груза , силы тяжести элементов блока и сила реакции в подшипнике O. Силы тяжести точек блока заменим равнодействующей , приложенной к центру его тяжести, совпадающим с центром O.

Кроме этого, на человека, груз и блок, действуют силы натяжения каната. Однако они не являются внешними. В теорему моментов, которую мы собираемся использовать, входят только внешние силы. Если бы мы учли внутренние силы, то, согласно третьему закону Ньютона, они возникали бы парами и взаимно сокращались.

3. Находим сумму моментов внешних сил, действующих на систему относительно оси вращения Oz. Силы и проходят через ось вращения, поэтому их моменты равны нулю. Момент от равен произведению абсолютного значения силы на плечо :   . Аналогичным способом находим момент силы :   . Только здесь момент отрицательный, поскольку сила закручивает блок в направлении, противоположном положительному направлению угловой скорости . Окончательно имеем.
;
.

4. Находим главный момент количества движения системы относительно оси Oz. Он равен сумме моментов тел, составляющих систему:
.
Моменты количества движения материальных точек A и B вычисляем тем же способом, что и моменты сил. Только вместо векторов сил используем векторы скоростей точек, умноженных на массы. Скорость приложена к точке A. Ее плечо, относительно оси вращения, равно . Поскольку вектор закручивает блок в направлении, противоположном положительному направлению угловой скорости, то момент количества движения точки A отрицательный:   . Аналогично находим момент количества движения точки B:   . Блок является твердым телом. Его момент количества движения находим по формуле:   . Поскольку блок является круглым, и его масса равномерно распределена по ободу, то момент инерции блока определяется по формуле:   . Так как проскальзывание отсутствует, то скорость точек обода блока равна скорости движения точек каната, которая равна скорости прикрепленного груза B. Отсюда находим угловую скорость блока:   . Вычисляем главный момент количества движения системы.

;
(2.1)   .

В формулу (2.1) входит скорость движения человека A относительно неподвижной системы координат. Однако нам известна только скорость его движения относительно каната. Чтобы выразить через , рассмотрим движение человека как сложное. При таком движении человек движется относительно каната со скоростью , направленную вверх, а канат движется со скоростью , направленную вниз. Тогда будет относительной скоростью, , а – переносной, . По теореме о сложении скоростей при сложном движении точки имеем:
.
Спроектируем это векторное уравнение на ось , и подставим в (2.1):
;

;
(2.2)   .

5. Применяем теорему об изменении кинетического момента системы.
;
.
Мы получили простейшее дифференциальное уравнение. Его решением является посоянная:
.
Подставляем (2.2):
.
Определим значение постоянной из начального условия. Известно, что в начальный момент времени , система покоилась. Подставляем :
.
Отсюда . Тогда
;
.

Ответ

Груз будет двигаться вверх со скоростью
.

Использованная литература:
И. В. Мещерский, Сборник задач по теоретической механике, Москва, «Наука», 1986.

Автор: Олег Одинцов.     Опубликовано: 18-03-2023