Принцип Даламбера (кинетостатика). Решение задачи

Рассмотрены законы, применяемые при решении задач методом кинетостатики. Приводится пример решения задачи, используя принцип Даламбера на определение реакций опор вращающегося вала. Приводится решение задачи двумя способами – применяя принцип Даламбера к стержню как к системе материальных точек, и как к твердому телу.

Основные законы, применяемые в кинетостатике

Принцип Даламбера для системы материальных точек

Сила инерции материальной точки

– это вектор , равный произведению массы m точки на ее ускорение , взятое с обратным знаком:
.

Принцип Даламбера для твердого тела

Для твердого тела можно воспользоваться законами преобразования сил, и привести силы инерции, действующие на материальные точки, из которых состоит тело, к неподвижному, произвольным образом выбранному центру . В результате они будут представлены силой инерции (главным вектором) , приложенной к этому центру и моментом сил инерции (главным моментом) относительно этого центра.

Главный вектор сил инерции не зависит от центра приведения. Главный момент – зависит.

Приведение сил инерции к центру масс тела

Наиболее удобным центром для приведения сил инерции является центр масс тела. При этом можно выбрать как неподвижную систему отсчета, начало которой в рассматриваемый момент времени совпадает с центром масс, так и подвижную систему, совершающую поступательное движение, начало которой находится в центре масс тела. Такой особенностью обладает только центр масс тела. Для других точек, мы должны использовать только неподвижные системы отсчета.

При приведении к центру масс, силы инерции представлены силой (главным вектором сил инерции) , приложенной к центру масс тела, и пары сил с моментом (главным моментом сил инерции относительно центра масс). Сила инерции выражается через массу тела и ускорение его центра масс по формуле:
.
Момент сил инерции определяется через производную по времени от момента количества движения тела относительно центра масс:
.
Компоненты момента количества движения выражаются через компоненты тензора инерции тела относительно центра масс и компоненты угловой скорости вращения тела:
.
При этом всегда можно так выбрать направления системы координат, при которых тензор имеет диагональный вид, то есть имеет максимум три отличные от нуля компоненты: .

Случай параллельных ускорений

Рассмотрим случай, когда ускорения всех точек твердого тела имеют одинаковое направление. Разобьем тело на бесконечно большое число элементов. Пусть – масса – го элемента; – его ускорение. Тогда на каждый элемент действует сила инерции . Поскольку все ускорения параллельны, то силы инерции также параллельны. Поэтому они имеют равнодействующую, которую обозначим как .

Вектор равнодействующей выражается через массу m тела и ускорение его центра масс (который совпадает с центром тяжести):
.
Абсолютная величина равнодействующей:
.

Точка приложения равнодействующей находится в центре параллельных сил, радиус-вектор которой вычисляется тем же способом, что и центр тяжести тела. Только вместо сил тяжести элементов используются силы инерции:
.
Стоит обратить внимание на то, что точка приложения равнодействующей сил инерции, в общем случае, не совпадает с центром тяжести тела. Они совпадают, когда ускорения всех точек тела равны. Тогда силы инерции, как и силы тяжести, пропорциональны массам точек. В остальных случаях совпадения нет.

Для определения положения точки приложения равнодействующей сил инерции можно применять те же методы, что и для определения положения центра тяжести. Так если тело является тонким стержнем, то можно построить эпюру распределенных сил инерции. Тогда точка приложения равнодействующей будет находиться в центре тяжести эпюры.

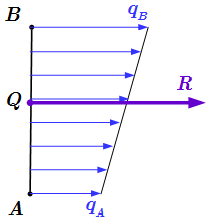
Рассмотрим распространенный случай, когда эпюра сил инерции представляет собой трапецию с интенсивностями на концах стержня .
Тогда расстояние от центра тяжести эпюры до конца A определяется по формуле:
.

Если , то эпюра представляет собой прямоугольник. Равнодействующая приложена к середине стержня: .

Если , то эпюра представляет собой треугольник. Равнодействующая проходит через центр тяжести треугольника, который совпадает с точкой пересечения его медиан:
.

Пример решения задачи. Определение реакций вращающегося вала

Условие задачи

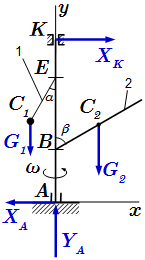
Вертикальный вал AK, вращающийся равномерно с угловой скоростью ω = 10 с^-1, закреплен подпятником в точке A и цилиндрическим подшипником в точке K.

К валу жестко прикреплены невесомый стержень 1 длиной l₁ = 0,3 м, на свободном конце которого расположен груз массой m₁ = 4 кг, и однородный стержень 2 длиной l₂ = 0,6 м, имеющий массу m₂ = 8 кг. Оба стержня лежат в одной вертикальной плоскости. Точки прикрепления стержней к валу, а также углы α и β заданы. Размеры AB=BD=DE=EK=b, где b = 0,4 м. Груз принять за материальную точку.

Пренебрегая массой вала, определить реакции подпятника и подшипника.

Решение

Дано:   с^-1, м, м, кг, кг, м, .

Найти: Реакции подпятника и подшипника.

Решение, применяя принцип Даламбера к системе материальных точек

Внешние силы

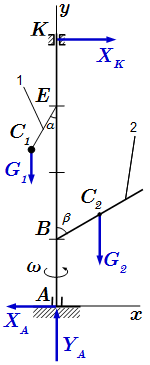
Рассмотрим внешние силы, действующие на вал. Проводим оси координат x, y. Ось z направим перпендикулярно плоскости рисунка на нас. Она не показана, поскольку, в рассматриваемый момент времени, все силы лежат в плоскости .

Рассмотрим силы тяжести, действующие на груз и стержень.
Поскольку стержень 1 можно считать невесомым, а груз – материальной точкой, то сила тяжести приложена на конце стержня 1, в точке , совпадающей с положением груза. Численное значение силы тяжести:
Н.

Сила тяжести, действующая на однородный стержень 2, равномерно распределена вдоль длины стержня. Она имеет равнодействующую, с абсолютным значением
Н.
Равнодействующая приложена в центре тяжести стержня. Поскольку он однородный, то центр тяжести находится по середине стержня – в точке :
м.

В опорах A и K отбрасываем связи, и вводим вместо них силы реакций. Реакцию в подпятнике разложим на две составляющие вдоль осей координат: X_A, Y_A. Реакция в цилиндрическом подшипнике K имеет одну горизонтальную составляющую X_K.

Силы инерции

Для определения реакций, применим принцип Даламбера. Для этого вводим силы инерции.

Сила инерции груза

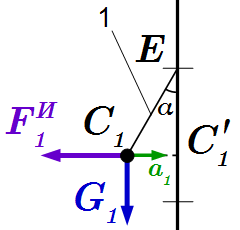
Найдем ускорение груза. Точка движется по окружности, вращаясь вокруг оси вала с постоянной угловой скоростью . Из точки опустим перпендикуляр на ось вала. Его длина равна радиусу окружности:
м.
Поскольку вращение равномерное, то ускорение груза имеет только нормальную составляющую, направленную к оси вала. Находим ее величину:
м/с².
Вводим силу инерции груза . Ее абсолютное значение:
.
Вектор силы инерции направлен противоположно ускорению , то есть противоположно оси .

Сила инерции стержня

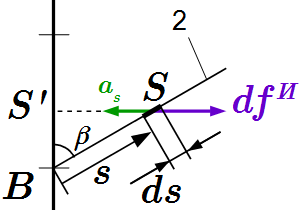
Рассмотрим стержень 2. Разобьем его на бесконечно большое число малых частей, которые будем считать материальными точками. Возьмем на стержне произвольную точку , находящуюся на расстоянии от конца стержня B. Рассмотрим малый элемент стержня длиной , примыкающий к точке S. Его масса: , где – линейная плотность стержня. Расстояние до оси вращения:
.
Ускорение элемента направлено к оси вращения. Его абсолютная величина
.
Сила инерции противоположна ускорению, и по абсолютной величине равна
.
Отсюда видно, что силы инерции всех элементов стержня направлены в одну сторону, от оси стержня, и распределены вдоль длины стержня по линейному закону:
.

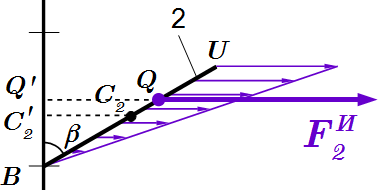
Поскольку силы инерции всех элементов стержня параллельны, то они имеют равнодействующую, которую мы обозначим, как . Ее абсолютная величина выражается через ускорение центра масс стержня, который всегда совпадает с центром тяжести. Поскольку стержень однородный, то его центр масс находится посередине: . Тогда

Н.

Точка приложения равнодействующей находится в центре тяжести эпюры. Поскольку она является треугольником, то центр тяжести эпюры находится в точке пересечения его медиан, на расстоянии от вершины :
.

Силу и точку ее приложения можно определить и другим способом – непосредственным интегрированием. Абсолютная величина равнодействующей равна сумме сил инерции всех элементов стержня. При стремлении к нулю, эта сумма превращается в интеграл:

.
Точкой приложения является центр параллельных сил. Его положение определяется аналогично положению центра тяжести:

.

Решение задачи статики

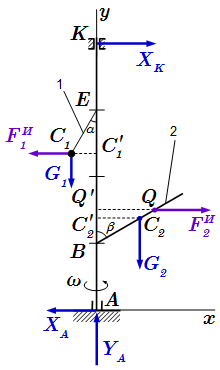
После введения сил инерции, мы получили задачу статики, в которой на конструкцию действуют силы реакции , силы тяжести и силы инерции . Требуется найти значения сил реакций, при которых система сил находится в равновесии.

Составляем уравнения равновесия.
Сумма проекций сил на ось координат равна нулю.
(1)   ;
(2)   .
Сумма моментов сил относительно оси , проходящей через точку A перпендикулярно плоскости рисунка (на нас) равна нулю.
(3)  
.

Решаем систему уравнений. Вычисляем расстояния.
;
;
;
;
.
Из уравнения (3), (1), (2) находим:

;
;
.

Ответ

.
Отрицательное значение реакции указывает на то, что ее направление противоположно указанному на рисунке.

Решение задачи, применяя принцип Даламбера к твердому телу

При решении задачи первым способом, мы воспользовались тем, что ускорения точек стержня параллельны. Это дало нам возможность заменить распределенные силы инерции равнодействующей. Кроме этого, эпюра сил инерции имела простой вид. Поэтому мы нашли точку приложения равнодействующей, не прибегая к сложным вычислениям. Решим эту задачу общим способом, который можно применить к любому твердому телу.

Мы имеем ту же систему внешних сил, состоящую из сил тяжести и реакций опор . Тем же способом определяем силу инерции груза, который считаем материальной точкой. Различие будет заключаться в методе определения сил инерции стержня.

При решении вторым способом, приведем силы инерции к центру масс стержня. Силы инерции стержня 2 представим в виде силы , приложенной к его центру масс, и пары сил с моментом .

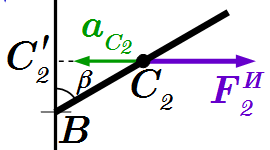
Силу инерции определяем через ускорение центра масс стержня, как и в первом способе, по формуле:
.
Поскольку стержень однородный, то его центр масс находится посередине стержня, на расстоянии от точки B. Тогда точка движется по окружности радиуса   с постоянной угловой скоростью . Ее ускорение – центростремительное, направленное к оси вала,
.
Сила инерции приложена к центру масс стержня, ее абсолютная величина:
.

Кроме силы инерции вводим момент сил инерции по формуле:
,
где – момент количества движения стержня относительно его центра масс. Его компоненты выражаются через компоненты тензора инерции стержня относительно центра масс и компоненты угловой скорости вращения:
(4)   .

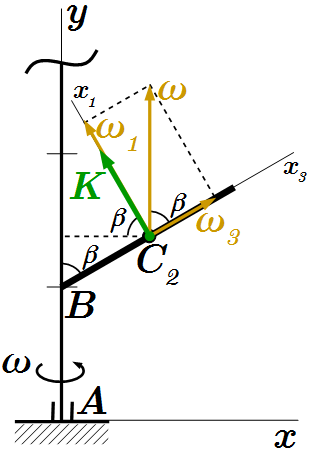
Для применения этой формулы, выберем систему координат , в которой тензор имеет диагональный вид. Начало этой системы, в рассматриваемый момент времени, находится в центре масс ; ось направлена вдоль стержня; оси – перпендикулярны. Пусть ось лежит в плоскости рисунка, а ось – перпендикулярна и направлена на нас (на рисунке не показана). В этой системе координат отличны от нуля только две компоненты: . Остальные компоненты равны нулю.

Поскольку вал вращается вокруг оси , то вектор угловой скорости направлен вдоль этой оси, то есть вверх. Тогда угловая скорость имеет следующие компоненты в системе координат :
.

Найдем в этой системе координат компоненты вектора момента количества движения стержня по формуле (4).
;
;
.
Отсюда видно, что вектор момента количества движения имеет только одну отличную от нуля компоненту:
.
То есть вектор , в рассматриваемый момент времени, направлен вдоль оси , перпендикулярно стержню.

Поскольку рассматриваемый момент времени произволен, то это означает, что абсолютная величина вектора момента количества движения стержня постоянна:
.
Вектор момента количества движения стержня лежит в плоскости вала перпендикулярно стержню, и вращается вместе с валом вокруг оси с угловой скоростью .

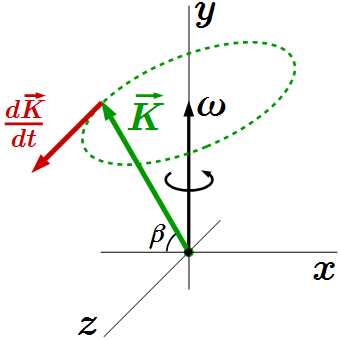
Для определения производной по времени вектора , отложим его из неподвижного начала. Тогда конец вектора будет вращаться по окружности радиуса вокруг оси с угловой скоростью . Скорость движения его конца и будет скоростью изменения вектора со временем, то есть будет равна производной вектора по времени. Отсюда заключаем, что производная направлена по касательной к окружности, и по абсолютной величине равна произведению угловой скорости на радиус окружности:
.

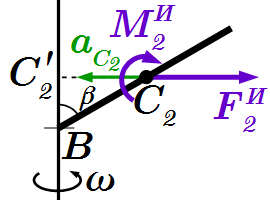
Тогда момент сил инерции , направлен перпендикулярно плоскости вала, от нас, и по абсолютной величине равен


.

Можно убедиться, что сила , приложенная в центре тяжести эпюры эквивалентна системе сил, состоящей из силы , приложенной в центре масс и паре с моментом .

Действительно, чтобы перенести точку приложения силы из в , к ней нужно добавить момент .
Здесь
.
Величина момента совпадает с . Поэтому сила инерции , приложенная в точке эквивалентна системе сил, состоящей из силы , приложенная в точке и паре сил с моментом .

Задача статики. Второй способ

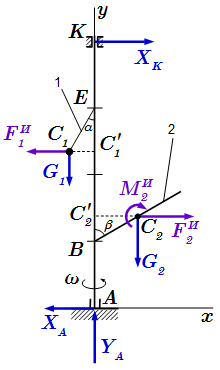
После введения сил инерции, мы получили задачу статики, в которой на конструкцию действуют силы реакции , силы тяжести , силы инерции и момент инерции . Во втором способе мы получили такую же систему сил за исключением того, что равнодействующую силу инерции стержня, приложенной в точке мы заменили на силу инерции стержня приложенную к центру масс и момент инерции . Требуется найти значения сил реакций, при которых система сил находится в равновесии.

Составляем уравнения равновесия.
Сумма проекций сил на ось координат равна нулю.
(1′)   ;
(2′)   .
Сумма моментов сил относительно оси , проходящей через точку A перпендикулярно плоскости рисунка (на нас) равна нулю.
(3′)  
.

Решаем систему уравнений. Вычисляем расстояния.
;
;
;
;

.
Из уравнения (3), (1), (2) находим:

;
;
.

Ответ

.

Использованная литература:
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.

Автор: Олег Одинцов.     Опубликовано: 22-06-2022