Решение задач на применение теоремы об изменении количества движения системы

Приводится инструкция, как решать задачи на применение теоремы об изменении количества движения системы. Рассмотрен пример решения задачи.

Как решить задачу на применение теоремы об изменении количества движения системы

1. Выбрать инерциальную (неподвижную) прямоугольную систему координат, скажем Oxyz.
2. Изобразить на рисунке все внешние силы , действующие на элементы системы, и записать их векторную сумму в общем виде:
   (1.1)   .
3. Определить, в каком направлении происходит движение, и спроектировать все внешние силы и их сумму (1.1) на это направление.
4. Изобразить на рисунке скорости точек или центров масс тел, составляющих систему относительно неподвижной системы координат (абсолютные скорости).
5. Если точка или тело движется относительно другого тела, и, если это удобно или задано в условии, то ввести относительную скорость точки или центра масс тела, и изобразить ее на рисунке. Далее найти абсолютную скорость этой точки, применяя теорему о сложении скоростей:
   (1.2)   ,
   где – переносная скорость точки или центра масс тела, совершающего относительное движение. Переносная скорость – это скорость точки тела, относительно которого совершается движение.
6. Составить вектор количества движения в общем виде:
   (1.3)   .
   Затем спроектировать его на направление движения и выразить через неизвестные величины.
7. Применить теорему об изменении количества движения системы:
   (1.4)   .
   Спроектировать это уравнение на направление движения и подставить полученные ранее выражения для проекций и .
8. В результате мы получим одно дифференциальное уравнение. Если имеется только одна неизвестная величина, то, мы ее сможем определить, решая это уравнение.
9. Если система совершает движение в двух или трех взаимно перпендикулярных направлениях, то получим два или три уравнения. Из них можно определить две или три неизвестные величины.
10. Если число неизвестных больше числа уравнений, то их нельзя найти, используя только теорему об изменении количества движения системы. Для решения задачи нужно составить дополнительные уравнения, применяя другие законы механики.

Задача. Определение скорости плиты с движущимся по ней грузом

Условие задачи

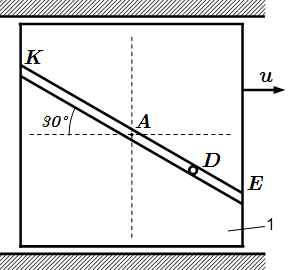
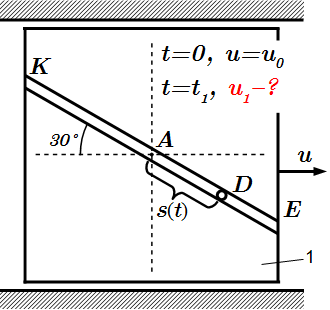
Механическая система состоит из прямоугольной вертикальной плиты 1 массой m₁=24 кг, движущейся вдоль горизонтальных направляющих, и груза D массой m₂=6 кг. В момент времени t₀=0, когда скорость плиты u₀=0,5 м/с, груз под действием внутренних сил начинает двигаться по желобу плиты.

Желоб прямолинейный и при движении груза расстояние s=AD изменяется по закону , где выражено в метрах; – в секундах. На рисунке груз D показан в положении, при котором s>0; при s<0 груз находится по другую сторону от точки A.

Считая груз материальной точкой, и пренебрегая всеми сопротивлениями, определить скорость плиты u₁ в момент времени t₁=1с.

Указания. Эта задача – на применение теоремы об изменении количества движения системы.

Краткое решение

;
;
;
;
;
кг;
;
.
При .
;
.
При м/с;
м/с.

Подробное решение с объяснениями

Дано:   m₁=24 кг, m₂=6 кг, t₀=0 с, u₀=0,5 м/с, м, t₁=1 с.
Найти: u₁.

Рассмотрим механическую систему, состоящую из плиты 1 и груза . Применим к ней теорему об изменении количества движения (1.4):
(2.1)   .
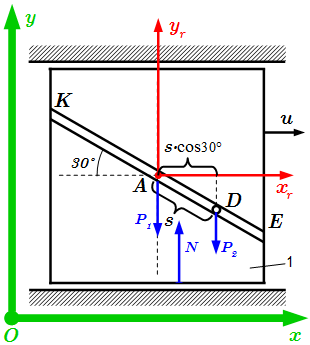
Выберем неподвижную систему координат . Ее начало возьмем произвольно. Ось направим горизонтально, ось – вертикально вверх.

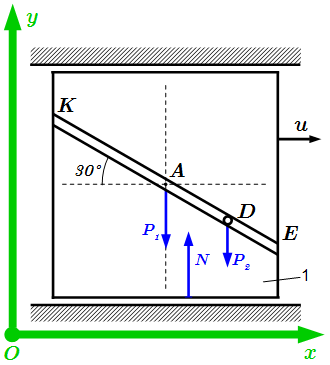
Рассмотрим внешние силы , действующие на систему. Это силы тяжести плиты и груза, направленные вниз; силы реакции направляющих. Силу тяжести плиты заменим равнодействующей , приложенной к ее центру тяжести. Сила тяжести груза приложена к грузу, который мы считаем материальной точкой. Поскольку трение отсутствует, то силы реакции направляющих направлены вертикально вверх, вдоль оси y. Поскольку они параллельны, то имеют равнодействующую , которая также направлена вдоль оси y.

Кроме сил тяжести на груз действуют силы реакции со стороны плиты и силы, приводящие груз в движение. Но они не являются внешними. Точно такие же силы по величине, но обратные по направлению действуют на плиту со стороны груза. Поэтому, при рассмотрении движения системы в целом, эти силы взаимно уничтожаются. В теорему об изменении количества движения системы входят только внешние силы, действующие на элементы системы.

Все внешние силы направлены вертикально. Поэтому их проекции на ость x равны нулю: . Спроектируем уравнение (2.1) на ось x.
;
.
Это простейшее дифференциальное уравнение. Из него следует, что проекция количества движения на ось x постоянная, не зависящая от времени величина.
.
Применяя формулу (1.3) находим:
(2.2)   .

Здесь – это скорость центра масс плиты. Она направлена вдоль направляющих, по оси x:
.
Поскольку плита совершает поступательное движение, то скорости всех ее точек также равны .

Груз D совершает составное движение. Он движется относительно плиты по заданному закону; плита совершает движение относительно инерциальной системы координат . По теореме о сложении скоростей, имеем:
(2.3)   .

Переносная скорость груза – это скорость движения точки плиты, в которой находится груз. У нас скорости всех точек плиты равны, поэтому
(2.4)   .

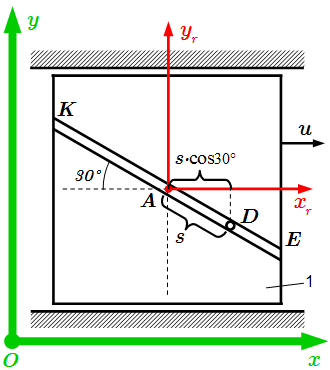
Относительная скорость – это скорость движения груза в системе координат (возможно неинерциальной), в которой плита покоится. Для ее математического описания, выберем систему координат , связанную с плитой. Ее начало поместим в центр плиты A. Тогда
.
Здесь – единичный вектор, направленный вдоль желоба ;
– заданный закон движения груза. Дифференцируя по времени, находим относительную скорость груза:
Спроектируем это векторное уравнение на ось :
;
(2.5)   .

Подставляем (2.4): , (2.5) в (2.3):
(2.6)   .
Подставляем и (2.6) в (2.2):
;
;
(2.7)   ,
где кг.

Находим производную, применяя правило дифференцирования сложной функции.
Пусть . Тогда
;
;
;
(2.8)   .

Подставим в (2.7) .
При , ,
,
(2.9)   .

Как мы выяснили, – постоянная, не зависящая от времени величина. Подставим ее значение (2.9) в формулу (2.7), справедливую для произвольного момента времени, и выполним преобразования.
;
(2.10)   ,
где зависимость от времени скорости определяется по формуле (2.8).

Формулы (2.10) и (2.8) определяют скорость плиты в произвольный момент времени. Находим ее значение в момент времени с.
При ,
,
.

Ответ

м/с.

Автор: Олег Одинцов.     Опубликовано: 13-12-2022   Изменено: 27-09-2023