Теорема о движении центра масс системы. Решение задач

Задача. Найти перемещение плиты и реакцию направляющих.

Приводятся формулы и законы, применяемые при решении задач с помощью теоремы о движении центра масс системы. Рассмотрены примеры решения задач. В одной задаче требуется найти смещение плиты с движущимися по ней грузами и реакцию направляющих. В другой задаче нужно найти вертикальную составляющую реакции в точке крепления кривошипно-шатунного механизма с ползуном.

Содержание

Основные законы, применяемые при решении задач

Теорема о движении центра масс

Центром масс механической системы: называется точка, радиус-вектор которой определяется по формуле:
(1) .
Здесь – радиус-вектор точки массой ; – масса механической системы.

Дифференцируя (1) по времени, находим.
(2) – скорость центра масс системы;
(3) – ускорение центра масс системы.
Здесь
– скорости точек или центров масс тел;
– ускорения точек или центров масс тел.

Теорема о движении центра масс механической системы

Пусть

– радиус-вектор центра масс механической системы.
Произведение массы системы на ускорение ее центра масс равно векторной сумме всех действующих на систему внешних сил:

Сложное движение точки

Входящие в (2) и (3) скорости и ускорения определяются относительно неподвижной системы отсчета. Часто возникают случаи, когда точки и тела совершают сложное движение. Например, точка движется относительно тела по заданному закону, а тело, в свою очередь, совершает движение относительно неподвижной системы отсчета. В этом случае удобно разбить движение на две составляющие – переносное и относительное. То есть удобно выбрать дополнительную подвижную систему отсчета. Тогда движение точек этой подвижной системы называется переносным, а движение точек относительно нее – относительным.

Абсолютная скорость (ускорение) точки: – это скорость (ускорение) точки в неподвижной системе координат.
Переносная скорость (ускорение) точки: – это скорость (ускорение) той точки подвижной системы координат, в которой, в данный момент времени, находится точка, совершающая сложное движение.
Относительная скорость (ускорение) точки: – это скорость (ускорение) точки относительно подвижной системы координат.

Теоремы о сложении скоростей и ускорений

При составном движении
абсолютная скорость

и ускорение

точки выражаются через переносные

и относительные

скорости и ускорения по формулам:

(теорема о сложении скоростей);

(теорема Кориолиса).
Здесь

– кориолисово ускорение;

– угловая скорость вращения подвижной системы координат.

Задача. Определение перемещения и реакции плиты с грузами

Условие задачи

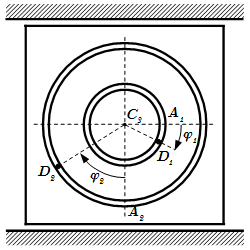
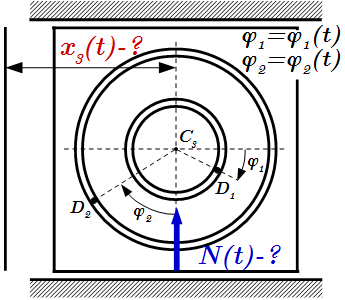
Механическая система состоит из груза D₁ массой m₁=3 кг и D₂ массой m₂=6 кг и из прямоугольной вертикальной плиты массой m₃=10 кг, движущейся вдоль горизонтальных направляющих. В момент времени t₀=0, когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобам, представляющим собой окружности радиусов r=0,4 м и R=0,8 м.

При движении грузов угол φ₁=A₁C₃D₁ изменяется по закону , а угол φ₂=A₂C₃D₂ – по закону . φ выражено в радианах, t – в секундах.

Считая грузы материальными точками, и пренебрегая всеми сопротивлениями, определить закон движения плиты x₃=f₃(t) и полной нормальной реакции направляющих N=f(t). x₃ – координата центра C₃ плиты.

Указания. Эта задача – на применение теоремы о движении центра масс. При этом для определения x₃=f₃(t) составить уравнение в проекции на горизонтальную ось x, а для определения N – на вертикальную ось y.

Решение

Дано: m₁=3 кг, m₂=6 кг, m₃=10 кг, t₀=0, r=0,4 м, R=0,8 м, , .

Найти: x₃=f₃(t), N=f(t).

Рассмотрим механическую систему, состоящую из плиты и грузов . Применим к ней теорему о движении центра масс:
(1.1) .
Здесь – ускорение центра масс системы; – внешние силы; – масса системы.

Выберем неподвижную систему координат . Ее начало выберем произвольно. Но чтобы ось проходила через центр плиты . Ускорение в теореме о движении центра масс определяется именно в неподвижной системе.

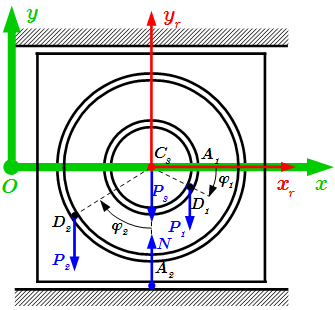
Неподвижная и подвижная системы координат, связанная с плитой

Рассмотрим внешние силы, действующие на систему. Это силы тяжести грузов ; сила тяжести плиты; и реакция направляющих . Силы тяжести направлены вертикально вниз. Будем считать, что реакция направлена вертикально вверх.

Кроме сил тяжести на грузы действуют силы реакции со стороны плиты и силы, приводящие грузы в движение. Но они не являются внешними. Точно такие же силы по величине, но обратные по направлению действуют на плиту со стороны грузов. Поэтому, при рассмотрении движения системы в целом, эти силы взаимно уничтожаются. В теорему о движении центра масс входят только внешние силы, действующие на элементы системы.

Спроектируем векторное уравнение (1.1) на оси системы координат .
;
.
Выразим эти уравнения через компоненты радиус-вектора центра масс учитывая, что :
(1.2) ;
(1.3) .

Определение закона движения плиты

Рассмотрим уравнение (1.2). Из него следует, что ускорение проекции центра масс на ось x равно нулю:
.
Это простейшее дифференциальное уравнение второго порядка. Оно имеет решение
(1.4) ,
где – постоянные, не зависящие от времени величины.

По формуле (1) выразим - координату центра масс системы через координаты грузов и координату центра масс плиты :
.
Подставляя в (1.4) находим:
(1.5) .

В условии задачи, нам заданы законы движения грузов относительно плиты, которая сама совершает движение. Поэтому выберем еще одну систему координат , связанную с плитой. За начало отсчета возьмем центр плиты . Оси направим параллельно осям .

Из векторного уравнения

выражаем координаты точки в неподвижной системе отсчета через координаты центра плиты в неподвижной системе и координаты точки в подвижной системе:
(1.6) .
Аналогично для точки :
(1.7) .

Проектируя отрезки и на оси , находим координаты грузов в подвижной системе координат.
;
(1.8) ;
;
(1.9) .
Здесь и являются заданными функциями от времени:
(1.10) .

Подставляем полученные соотношения в (1.5), и выполняем преобразования.
;
;
;
(1.11) .

Постоянные определим из условия, чтобы в начальный момент времени , центр плиты находился в начале координат , и чтобы скорость плиты равнялась нулю: .

Подставляем в (1.10) .
;
.
Подставляем в (1.11) .
;
;
;
.

Дифференцируем (1.11) по времени.
;
;
;
;

.
Подставляем .
;
;
;
;
.

Окончательно имеем.

.

Определение реакции направляющих

Из уравнения (1.3) находим:
(1.12) ,
где
.

По формуле (1) выражаем - координату центра масс системы через координаты грузов и координату центра масс плиты :
.
Поскольку , то
.
По формулам (1.6), (1.7), (1.8), (1.9), выражаем координату центра масс системы через углы .
.

Дифференцируем по времени.
;
;
;
;
;
;

;

;
;
;

.

Подставим в (1.12) и преобразуем окончательно.

.

Ответ

;
;
.
Здесь выражено в метрах; – в Ньютонах; – в секундах.

Задача. Определение реакции в кривошипно-шатунном механизме

Условие задачи

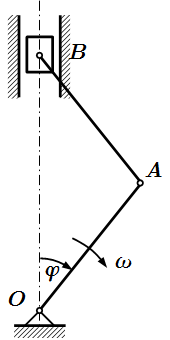
В кривошипно-шатунном механизме кривошип OA и шатун AB представляют собой однородные стержни массой m₁ и длиной l. Ползун B массой m₂ движется в вертикальных направляющих. Определить вертикальную составляющую реакции шарнира O в функции угла φ, если кривошип вращается с постоянной угловой скоростью ω. Трением в направляющих ползуна пренебречь.

Решение

Дано: m₁, m₂, |OA| = |AB| = l, ω.

Найти: N_y(φ).

Рассмотрим механическую систему, состоящую из кривошипа OA, шатуна AB и ползуна B. Применим к ней теорему о движении центра масс:
(2.1) .
Здесь – ускорение центра масс системы; – внешние силы; – масса системы.

Выберем систему координат с началом в шарнире O. Ось Oy направим вдоль направляющих ползуна.

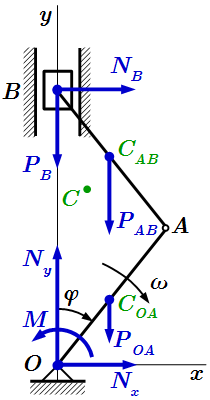
Внешние силы, действующие на систему, состоящую из кривошипа, шатуна и ползуна — Внешние силы, действующие на систему

Рассмотрим внешние силы, действующие на систему. Это момент сил M, действующий на кривошип, поддерживающий угловую скорость ω постоянной; силы тяжести кривошипа, шатуна и ползуна, направленные вертикально вниз, противоположно оси Oy; сила реакции шарнира O; сила реакции направляющих. Поскольку трением в направляющих можно пренебречь, то сила направлена перпендикулярно направляющим, то есть перпендикулярно оси Oy. Силу реакции разложим на составляющие вдоль осей координат.

Подставим действовавшие на нашу систему силы в уравнение движения центра масс (2.1). .
Спроектируем это векторное уравнение на ось Oy.
;
.
Выразим ускорение центра масс через компоненты радиус-вектора центра масс .
;
.
Отсюда
(2.2) .

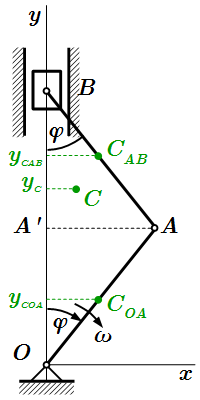
Центры масс шатуна, кривошипа и ползуна.

Компоненту радиус-вектора центра масс системы определим по формуле (1).

;
(2.3) .
Здесь – центры масс кривошипа и шатуна; – их - координаты. Ползун B мы считаем материальной точкой.

Поскольку кривошип OA и шатун AB являются однородными стержнями, то их центры масс делят стержни пополам.
.
Из геометрии находим - координаты центров масс тел.
;
;
.
Подставляем в (2.3).

;
(2.4) .

Дифференцируем (2.4) по времени учитывая, что угловая скорость является постоянной.
;
;
;
.

Отсюда находим вторую производную по времени - координаты центра масс системы.
.
Подставляя в (2.2), находим искомую вертикальную составляющую реакции шарнира.
.

Ответ

Автор: Олег Одинцов. Опубликовано: 08-10-2022