Термодинамические соотношения для сверхпроводников
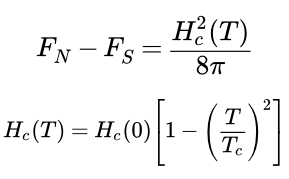
Основные формулы
Свободная энергия сверхпроводящего состояния ниже свободной энергии нормального состояния на величину
(1.1) ,
где – критическое магнитное поле.
Зависимость критического магнитного поля от температуры достаточно точно описывается эмпирической формулой
(1.2) .
Значения и для различных элементов приводятся в табл. 1.1. Для решения приведенных ниже задач необходимо применить некоторые термодинамические соотношения.
| Элемент | , К | , э |
|---|---|---|
| Al | 1,175±0,002 | 104,9±0,3 |
| Be | 0,026 | |
| Cd | 0,517±0,002 | 28±1 |
| Ga | 1,083±0,001 | 59,2±0,3 |
| Hf | 0,128 | |
| Hg(α) | 4,154±0,001 | 411±2 |
| Hg(β) | 3,949 | 339 |
| In | 3,408±0,001 | 281,5±2 |
| Ir | 0,1125±0,001 | 16±0,05 |
| La(α) | 4,88±0,02 | 800±10 |
| La(β) | 6,00±0,1 | 1096 |
| Lu | 0,1 | 400 |
| Mo | 0,915±0,005 | 96±3 |
| Nb | 9,25±0,02 | 2060±50 |
| Os | 0,66±0,03 | 70 |
| Pa | 1,4 | |
| Pb | 7,196±0,006 | 803±1 |
| Re | 1,697±0,006 | 200±5 |
| Ru | 0,49±0,015 | 69±2 |
| Sn | 3,722±0,001 | 305±2 |
| Ta | 4,47±0,04 | 829±6 |
| Tc | 7,8±0,01 | 1410 |
| Th | 1,38±0,02 | 160±3 |
| Ti | 0,40±0,04 | 56 |
| Tl | 2,38±0,04 | 178±5 |
| V | 5,40±0,05 | 1408 |
| W | 0,0154±0,0005 | 1,15±0,03 |
| Zn | 0,850±0,01 | 54±0,3 |
| Zr | 0,61±0,15 | 47 |
Задача 1.1
Какой ток течет по плоской поверхности свинца в полосе шириной 1 см, если образец находится в критическом поле при температуре 4,2 К?
Решение
Зависимость критического магнитного поля от температуры выражена формулой (1.2). Подставляя значения и из табл. 1.1, для свинца получим э.

Рассмотрим контур 1–2–3–4–1 на рис. 1.1, и возьмем циркуляцию вектора по этому контуру. На участке 1–2, который параллелен поверхности сверхпроводника, , где – длина участка 1–2. Вклад от участков 2–3 и 1–4 равен нулю, так как из соображений симметрии можно утверждать, что вектор на этих участках ортогонален пути интегрирования. Вклад участка 3–4 также нулевой, поскольку внутри сверхпроводника. Итак, . Но согласно уравнению Максвелла
,
где – полный ток, протекающий через поверхность, ограниченную контуром 1–2–3–4–1. Отсюда следует, что перпендикулярно плоскости чертежа в направлении “от нас” (так, как показано на рис. 1.1) по поверхности сверхпроводника течет поверхностный ток, величина которого
,
откуда А/см.
Задача 1.2
На сколько понизится свободная энергия 1 см3 свинца при его переходе в сверхпроводящее состояние? Переход происходит в магнитном поле при температуре 4,2 К.
Решение
Разность между свободной энергией нормального и сверхпроводящего состояний определяется по формуле (1.1). Используя данные э из задачи 1.1 найдем
эрг/см3.
Задача 1.3
Какое количество теплоты выделится при переходе 1 см3 свинца в сверхпроводящее состояние, если переход происходит в магнитном поле при температуре 4,2 К?
Решение
Учитывая, что энтропия (на единицу объема) нормальной и сверхпроводящей фаз определяется формулами
,
можем определить количество выделившегося тепла из соотношения:
.
Используя выражения (1.1) и (1.2), получаем:
.
Таким образом,
(1.3) ,
откуда
.
Подставив значения, получим эрг.
Задача 1.4
Найти температуру, при которой у свинца теплоемкости нормальной и сверхпроводящей фаз оказываются равными.
Решение
По определению теплоемкости ; используя формулу (1.3), имеем
.
Согласно условию задачи или
,
а это равенство выполняется только при двух значениях температуры: и К. Следовательно, искомая температура равна 4,115 К.
Задача 1.5
Найти критическое термодинамическое магнитное поле олова при температуре 3 К.
Решение
Подставляя данные для и в формулу (1.2), получим э.
Задача 1.6
Найти скачек теплоемкости единицы объема свинца при критической температуре.
Решение
Используя формулу, определяющую разность теплоемкостей нормального и сверхпроводящего состояний, полученную в задаче 1.4, имеем
.
Таким образом,
эрг/см3 К.
Далее Квантование потока и уравнения Лондонов
Оригинал




