Одномерные уравнения ГЛ и первый интеграл

Получение уравнений Гинзбурга Ландау в одномерном случае для однородного и бесконечно протяженного сверхпроводника, когда все физические величины зависят от одной координаты x. Граничные условия; первый интеграл.

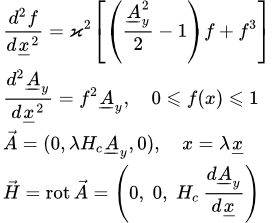
Основные результаты

Рассмотрим бесконечно протяженный сверхпроводник, помещенный во внешнее магнитное поле . Пусть справа, при расположена сверхпроводящая фаза, а слева – нормальная. И пусть все физические величины зависят только от координаты x.
1. Решение уравнений Гинзбурга-Ландау описывается двумя действительными функциями и , которые определяют безразмерную волновую функцию , , векторный потенциал , магнитное поле , а также плотность тока сверхпроводящих электронов ,
.
2. Неизвестные функции удовлетворяют следующим уравнениям:
(14)   ;
(13)   ,
где – квант потока,   – глубина проникновения магнитного поля,
.
3. Граничные условия.
При .
3.1. Если сверхпроводник не имеет границы, то при .
Поскольку уравнения не содержат x явно, то решение имеет вид , где C – постоянная. Поэтому нужно задать значение этой постоянной, наложив условие в конечной точке, например .
3.2. Если сверхпроводник ограничен диэлектриком при , то
.

Вывод уравнений

Рассмотрим бесконечно протяженный сверхпроводник, помещенный во внешнее магнитное поле, направленное вдоль оси z: . Рассмотрим уравнения Гинзбурга – Ландау для этого простого случая. Считаем, что все физические величины зависят только от координаты x. Пусть справа, при будет сверхпроводящее состояние, Тогда безразмерная волновая функция при . Слева, при – нормальная фаза.

Предположим, что в сверхпроводнике магнитное поле также направлено вдоль оси z:
(1)   .
Если это не так, то мы получим несовместные уравнения.

Используем уравнения Гинзбурга-Ландау для безразмерной волновой функции :
(2)     – первое уравнение ГЛ;
(3)     – второе уравнение ГЛ;
(4)     – граничное условие между сверхпроводником и диэлектриком.

Чтобы описать магнитное поле вида (1), достаточно положить . Тогда
(5)   .

Выражаем поле через потенциал .
;
.
Здесь штрих означает производную функции по ее аргументу: . Далее находим:
;
.

Волновая функция может зависеть от x, y и z. При этом плотность сверхпроводящих электронов, пропорциональная , зависит только от переменной .

Подставляя и во второе уравнение ГЛ, получаем три уравнения для x, y и z компонент.
(3)   ;
(6)   ;
(7)   ;
(8)   .

Выразим комплексную функцию через модуль и аргумент :
(9)   ,
Где и – действительные функции. При этом , как упоминалось выше, зависит только от переменной .

Подставим (9)  в  (6):
;   ;
(6)   ;
;
;
.
Но , поскольку она пропорциональна плотности сверхпроводящих электронов. Тогда . То есть не зависит от .

Аналогичным способом, из (8) заключаем, что не зависит от . То есть может быть функцией только от переменной y: . Таким образом, мы пришли к более простому виду функции :
(10)   .

Подставим (10) в (7).
(7)   ;
;   ;
;
;
.
Поскольку от переменной зависит только слагаемое, содержащее , то может быть только постоянной. Обозначим ее как
.
Тогда
(11)   ,
и предыдущее уравнение примет вид:
(12)   .

Далее мы можем еще более упростить вид волновой функции (11), если выполним калибровочное преобразование, которое, как известно, не меняет уравнений ГЛ. Делаем подстановки.
;
.
Положим , тогда
, откуда
.
То есть в качестве волновой функции можно взять вещественную величину, зависящую только от переменной x.

Для векторного потенциала имеем.
.

Подставляем в (12) и опускаем знаки тильды.
(13)   .
Здесь – вещественная функция.

Подставим в первое уравнение ГЛ:
(2)   ;


;
(14)   .

Результат

Итак, для одномерного случая, когда все физические величины зависят только от координаты x, а внешнее магнитное поле направлено вдоль оси z, мы нашли следующее.
1. Безразмерная волновая функция является действительной функцией, зависящей только от координаты x:
(15)   .
2. Векторный потенциал описывается одной компонентой, зависящей от x:
(16)   .
Магнитное поле имеет только z компоненту, равную производной по x:
(17)   .
3. Уравнения Гинзбурга-Ландау имеют следующий вид.
(14)   ;
(13)   .

Граничные условия

Не ограниченный сверхпроводник

Рассмотрим граничные условия для случая бесконечно протяженного, не ограниченного поверхностями сверхпроводника, помещенного во внешнее магнитное поле . Такой случай может быть полезен для исследования переходов между нормальной и сверхпроводящей фазами. Пусть сверхпроводящая фаза находится при , а нормальная, при .

Уравнения (14), (13) второго порядка с двумя неизвестными функциями. Поэтому их решение должно содержать четыре постоянных, которые определяются из граничных условий.

1. Поскольку при имеется сверхпроводящая фаза, то . Магнитное поле на бесконечности отсутствует. Поэтому . Из (14) следует, что при этом . Также можно считать, что равны нулю все производные этих функций на бесконечности: , и т.д..
2. Поскольку при имеется нормальная фаза, то .
3. Поскольку сверхпроводник помещен во внешнее магнитное поле, то ;
.
Отсюда
(18)   при , где C – постоянная.
4. Уравнения (14), (13) не содержат переменной x в явном виде. Поэтому их решения имеют вид , где C – постоянная. Эту постоянную можно задать произвольным образом, зафиксировав границу перехода. Например, можно положить . Или можно зафиксировать векторный потенциал, выбрав значение постоянной в (18). Например так:
при .

Мы получили больше четырех граничных условий, но не все они независимы. Часть из них следуют из самих уравнений, но их удобно применять в таком виде при построении решений.

Волновая функция заключена в пределах . При ее график выпуклый вниз и имеет асимптоту . При график выпуклый вверх с асимптотой .

Векторный потенциал: . Функция возрастает; график выпуклый вверх и имеет асимптоты при , и при .

Ограниченный сверхпроводник

Теперь рассмотрим сверхпроводник, ограниченный диэлектриком при . Сверхпроводящая фаза располагается при . При граничные условия такие как и для неограниченного сверхпроводника:
.

Рассмотрим условия при . Граничные условия для безразмерной волновой функции имеют вид:
,
где – вектор нормали поверхности. Подставляя сюда , находим:
(19)   .

Положим, что намагниченность обусловлена только сверхпроводящими электронами. Тогда поле непрерывно на границе раздела. Из (17) получаем:
.

Безразмерные уравнения

Можно еще упростить уравнения, если перейти к безразмерным уравнениям, выполнив подстановки:
;   ;
;
.

Тогда уравнения (14), (13) примут вид:
(14*)   ;
(13*)   .
Здесь дифференцирование производится по безразмерной переменной . Граничные условия указаны выше.

Первый интеграл

Можно найти один из интегралов уравнений (14*) и (13*). Воспользуемся тем, что
(20)   .
Из (14*) и (13*) имеем.
;
.
Заметим, что
;
.
Подставим в (20).

;
;
.

Отсюда получаем интеграл:
.
Если справа – сверхпроводящая фаза, то при . Тогда ;
(21)   .

Использованная литература:
О.Г. Одинцов, Е.А. Пушкарев, Методические указания к решению задач по физике сверхпроводников, Харьков, ХГУ, 1989.
Е.М. Лифшиц, Л.П. Питаевский, Статистическая физика. Часть 2. Теория конденсированного состояния, Москва, Физматлит, 2002.

Авторы: Олег Одинцов, Евгений Пушкарев.     Опубликовано: 05-08-2024