Уравнения Лондонов и квантование потока в сверхпроводниках

Приведены основные формулы, относящиеся к уравнениям Лондонов и квантованию магнитного потока в сверхпроводниках. Рассмотрены шесть задач. В их числе: квантование потока и магнитное поле в тонкой сверхпроводящей трубке; распределение магнитного поля и сверхпроводящего тока в пластине и цилиндре.

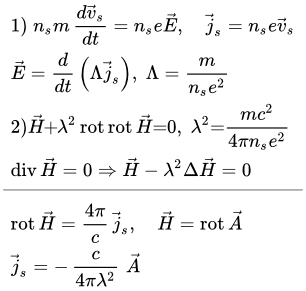
Основные формулы

Примечание. Под полем здесь и далее подразумевается истинное микроскопическое магнитное поле.

Представив волновую функцию сверхпроводящих электронов в виде

в выражении для плотности потока частиц в магнитном поле
(2.1)  
и воспользовавшись тем, что

( – плотность сверхпроводящих электронов, – плотность куперовских пар, – фаза волновой функции, – векторный потенциал), получим часто используемое соотношение
(2.2)   ,
с помощью которого можно показать, что поток квантуется. Квант потока определяется формулой
(2.3)    Гс·см².

Уравнения Лондонов позволяют получить распределение полей и токов в сверхпроводниках первого рода.

Первое уравнение Лондонов – уравнение движения электронов
(2.4)  
можно переписать в виде
(2.4*)   ,
где – плотность сверхпроводящего тока, .

Второе уравнение Лондонов получается из минимизации функционала
(2.5)  
(представляющего собой сумму энергий сверхпроводника в отсутствии магнитного поля , энергии магнитного поля и кинетической энергии сверхпроводящих электронов) и имеет вид
,
где
.
Полагая, , второе уравнение Лондонов примет вид:
(2.6)   .

Укажем также соотношение, связывающее плотность сверхпроводящего тока с векторным потенциалом:
(2.7)   .

Задача 2.1

В массивном сверхпроводнике имеется отверстие диаметром 0,1 мм, в котором захвачено 7 квантов магнитного потока. Определить напряженность магнитного поля в отверстии.

Решение

Поток магнитного поля , где – площадь отверстия. По условию задачи . Поэтому окончательно имеем:
.
Подставляя значение из (2.3),  см, получим  э.

Задача 2.2

В массивном сверхпроводнике имеется цилиндрическое отверстие диаметром 2 см. В нем захвачено магнитное поле с напряженностью H = 300 э. Найти величину векторного потенциала A на расстоянии  см от центра отверстия. Найти градиент фазы на этом же расстоянии .

Решение

Выразим магнитный поток через векторный потенциал (применяя теорему Стокса):
.
Интегрируя по окружности на расстоянии от центра отверстия, найдем
,
где  см – радиус отверстия в сверхпроводнике, а векторный потенциал
 э·см.

Для определения градиента фазы воспользуемся уравнением на собственные значения импульса (2.2) и проинтегрируем его по контуру, представляющему собой окружность радиуса . Учитывая, что , имеем:
,
откуда
 рад/см.

Задача 2.3. Квантование потока в тонкой сверхпроводящей трубке

Тонкая сверхпроводящая пленка толщины нанесена на поверхность диэлектрической нити. Радиус сечения нити R. Нить внесена в продольное магнитное поле при комнатной температуре, затем температура нити опущена ниже . После этого внешнее магнитное поле выключается. Как квантуется магнитный поток, захваченный нитью с пленкой?

Решение

Перепишем уравнение (2.2), воспользовавшись тем, что плотность потока :
.
Так как , то ток будет однородно распределен по толщине пленки. Проинтегрируем это уравнение по контуру, изображенному на рис. 2.1,
(2.9)   .

Раскрываем интегралы
.
Здесь – разность фаз, набегающая при обходе контура. Для того чтобы волновая функция была однозначной, необходимо выполнить условие , где n – целое число.

Во втором интеграле воспользуемся уравнением Максвелла для определения j:
;
(2.10)   .
Проинтегрируем это выражение по площадке , ограниченной контуром, изображенном на рис. 2.2. Получим
, откуда
.
Теперь вычисляем второй интеграл уравнения (2.9)
,
где использовано соотношение .
Третий интеграл равен потоку :
.
Таким образом, получим
,
откуда
.

Задача 2.4. Магнитное поле тонкой сверхпроводящей трубки

Найти распределение магнитного поля в условиях задачи 2.3.

Решение

Вне нити магнитное поле . Для определения поля внутри нити воспользуемся уравнением Максвелла
.

Интегрируя по контуру C₁ (рис 2.3), получим
.
Интегралы по перпендикулярным к поверхности участкам контура равны нулю. Следовательно, внутри нити поле постоянно
.

Для определения поля в пленке проинтегрируем по контуру C₂: . Вводим расстояние от центра нити. Площадь, ограниченная контуром: . Тогда
;
;
.
График дан на рис. 2.4.

Задача 2.5. Магнитное поле и ток в сверхпроводящей пластине

Найти распределение магнитного поля и ток в сверхпроводящей пластине толщиной d, которую поместили в магнитное поле .

Решение

Уравнение Лондонов (2.6)
сводится в данном случае к одномерному уравнению
,
которое имеет решение
.
Константы и определяем из граничных условий.
,
откуда . Таким образом
.

Сверхпроводящий ток определяем из уравнения Максвелла , откуда
.

Задача 2.6. Магнитное поле и ток сверхпроводящего цилиндра

Найти распределение магнитного поля и токов в сверхпроводящем цилиндре радиуса R, помещенного в однородное магнитное поле ( параллельно оси цилиндра).

Решение

Выбираем цилиндрическую систему координат. В силу симметрии все величины могут зависеть лишь от координаты . Уравнение Лондонов (2.6) для компоненты в этом случае примет вид
,
или
.
Этому дифференциальному уравнению удовлетворяют цилиндрические функции нулевого порядка мнимого аргумента. Общее решение можно записать в виде
.
Учитывая, что при , получим . Константу определяем из граничных условий
,
откуда
.

Распределение токов можно определить из компоненты уравнения:
.
Воспользовавшись рекуррентным соотношением
,
а также свойством , при целом , получим
.

Далее Уравнения Гинзбурга - Ландау

Оригинал