Определение функции распределения сверхтонкого магнитного поля по спектрам ядерного гамма резонанса

Для изучения свойств ферромагнитных материалов большой интерес представляет распределение сверхтонких магнитных полей. В данной работе предложен метод численного определения функции распределения, который приводит к повышению скорости расчетов и уменьшению занимаемой оперативной памяти ЭВМ, по сравнению с методами, применяемыми ранее.

В случае сильно концентрированных в не упорядоченных (аморфных) структур имеется большое число неэквивалентных положений резонансных ядер, что делает удобным интерпретацию результатов месбауэровского эксперимента в терминах Функции распределения сверхтонкого магнитного поля Р(Н). Известны два метода определения Р(Н) с помощью расчетов на ЭВМ [1, 2]. Для реализации первого из них необходим небольшой объем памяти, в то время как второй характеризуется значительно меньшим счетным временем ЭВМ. Предлагаемый в настоящей работе метод обладает преимуществами каждого из них, что особенно удобно при вычислении погрешностей и устранении нефизических отрицательных вероятностей.

Значения интенсивностей прошедшего излучения в зависимости от скорости определяется выражением
(1)   ,
где – интенсивность фонового излучения, а при использовании в качестве мессбауэровского ядра изотопа Fe⁵⁷
(2)   .
Здесь δ – изомерный сдвиг, – весовые и полевые коэффициенты соответственно, Γ – естественная ширина линии.

Интегральное уравнение (1) относится к классу некорректных задач. Общий метод решения состоит в том, что функцию Р(Н) разлагают в ряд по полной системе функций, оставляя первые m членов разложения:
(3)   ,
где – коэффициенты разложения, подлежащие определению. Подставляя ряд (3) в (1), имеем
.
Поскольку – подлежащая определению постоянная, то ее удобно обозначить через , а выражение примет вид
(4)   ,
где введены обозначения:
(5)   .
Для определения коэффициентов , необходимо отыскать минимум функционала [3]:
(6)   ,
где – значения экспериментальных интенсивностей, измеренных при скорости источника ; – параметр регуляризации, подбираемый по невязке
(7)  
(— дисперсия для экспериментальных точек при скорости источника).

К функциям предъявляют следующие требования: во-первых, ряд (3) должен по возможности быстро сходиться, что уменьшает объем работы ЭВМ, а, во-вторых, вычисление интегралов (5) должно занимать по возможности малое время.

В работе [1] предлагается использовать тригонометрические функции. Хотя ряд (3) имеет хорошую сходимость (), но интегралы (5) не выражаются через известные функции и требуется численное интегрирование, что сильно увеличивает время решения. В работе [2] поле H в пределах от нуля до H_max разбивается на N равных частей. представляет собой «ступеньку», которая равна нулю при и и равна единице в промежутке между и . Интегралы (5) вычисляются элементарно, но ряд (3) сходится плохо, так что , и решение P(H) получается разрывным.

В настоящей работе предлагается модернизировать метод [2] с тем, чтобы получить непрерывную функцию P(H) и улучшить сходимость ряда (3). Этого можно достичь, если в качестве P_l(H) выбирать функции, определяемые из выражений
при ;
при ;
при .
Решение P(H) имеет вид трапеций (см. рисунок). Интегралы (5) вычисляются элементарно и равны:

,
,

.

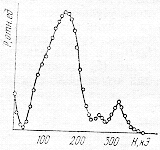
Анализ сходимости ряда (3) показывает (сравнивалось отклонение аппроксимации от точного решения в метрике С), что по сравнению с [2] количество разбиений по Н можно уменьшить в 2–4 раза. При этом понадобится в 2–4 раза меньше память ЭВМ и меньше машинного времени. В качество примера на рисунке представлен результат восстановления функции P(H) из экспериментальных спектров поглощения сплава на основе системы железо – хром. Из вида этой Функции можно сделать вывод о том, что структура сплава представляет собой – твердый раствор с величиной сверхтонкого магнитного поля H = 12,7 МА/м. Асимметричный характер P(H) свидетельствует о расслоении – твердого раствора, т. е. наличие в нем областей, обогащенных хромом (H<8 МА/М). Кроме того, увеличение Р(Н) при H=0 и H=26,5 МА/м свидетельствует о выделении в сплаве парамагнитной и богатой железом фаз соответственно.

Список литературы
1. Window B. Hyperfine field distributions from Mossbauer spectra // Journal of Physics E, 1971. 4. P. 401–402.
2. Hesse J., Rubartsch A. Model independent evaluation of overlapped Mossbauer spectra // Journal of Physics E, 1974. 7. P. 526–532.
3. Тихонов А. Н., Арсенин В. Я. Методы решения некорректных задач. М.: Наука, 1986. 120 с.

Поступила в редколлегию 18.03.88

Авторы: А. И. Великодный, О. Г. Одинцов, Е. А. Пушкарев.
Определение функции распределения сверхтонкого магнитного поля по спектрам ядерного гамма-резонанса.
Проблемы ядерной физики и космических лучей, № 31, 1989 г.

Оригинал