Арифметические свойства конечных пределов последовательностей

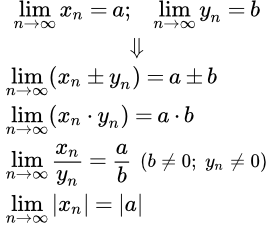
Формулировки арифметических свойств

Пусть существуют конечные пределы lim_{n → ∞} x_n  = a  и  lim_{n → ∞} y_n  = b  числовых последовательностей {x_n} и {y_n} .
Тогда существуют пределы суммы, разности и произведения последовательностей, которые равны, соответственно, сумме, разности и произведению их пределов.
Если  b ≠ 0  и  y_n ≠ 0  для всех n ,
то существует предел частного последовательностей, равный частному пределов:
(1)   lim_{n → ∞} (x_n  ± y_n ) = a ± b ;   Доказательство
(2)   lim_{n → ∞} (x_n  ⋅ y_n ) = a ⋅ b ;   Доказательство
(3)   lim_{n → ∞} x_ny_n = ab ,   если b ≠ 0 и y_n  ≠ 0 ;   Доказательство
(4)   lim_{n → ∞} (C ⋅ x_n ) = C ⋅ a .   Доказательство
Здесь C – постоянная, то есть заданное число.

Если lim_{n → ∞} x_n  = a ,
то lim_{n → ∞}  | x_n  |  =  | a |  .   Доказательство

Пусть существуют пределы lim_{n → ∞} x_n  = a и lim_{n → ∞} y_n  = b числовых последовательностей {x_n } и {y_n } .
Причем a ≠ ∞,  b ≠ 0 .
И пусть последовательность {α_n } бесконечно малая: lim_{n → ∞} α_n  = 0 ,
а последовательность {β_n } бесконечно большая: lim_{n → ∞} β_n  = ∞ .
Тогда существует пределы суммы и разности:
lim_{n → ∞} (β_n  ± x_n ) = ∞ ;
существуют пределы произведений:
lim_{n → ∞} (α_n  ⋅ x_n ) = 0,  lim_{n → ∞} (β_n  ⋅ y_n ) = ∞ ;
существуют пределы частного:
lim_{n → ∞} y_nα_n = ∞  при α_n  ≠ 0 ,
lim_{n → ∞} x_nβ_n = 0  при β_n  ≠ 0 .

Теорема о пределе суммы и разности числовых последовательностей

Все свойства Пусть существуют конечные пределы
lim_{n → ∞} x_n  = a  и  lim_{n → ∞} y_n  = b последовательностей {x_n } и {y_n } .
Тогда существуют пределы суммы и разности последовательностей {x_n ± y_n} , и они равны сумме и разности их пределов:
lim_{n → ∞} (x_n  ± y_n ) = lim_{n → ∞} x_n  ± lim_{n → ∞} y_n  = a ± b .

Чтобы доказать свойство суммы и разности (1), нам нужно найти такую функцию N(ε ) , при которой, для любого положительного числа ε > 0 , выполняется неравенство:
(1.1)    | x_n  ± y_n  – (a ± b ) |  < ε  при  n > N(ε ) .
При этом мы имеем функции N_x (ε₁ ) и N_y (ε₂ ) , при которых выполняются неравенства (5) и (6), для любых положительных ε₁ и ε₂ .

Воспользуемся известным неравенством
 | A + B |  ≤  | A |  +  | B |  .
Преобразуем модуль разности в (1.1) и применим (5) и (6):
 | x_n  ± y_n  – (a ± b ) |  =  | x_n  – a ± (y_n  – b ) |  ≤  | x_n  – a |  +  | y_n  – b |  < ε₁  + ε₂ .
Последнее неравенство справедливо при n > N_x (ε₁ )  и  n > N_y (ε₂ ) . Положим ε₁  = ε₂  = ε / 2 . Тогда, при n > N_x (ε / 2 )  и  n > N_y (ε / 2 ) ,
 | x_n  ± y_n  – (a ± b ) |  < ε .
Пусть, при заданном ε ,  N(ε ) есть наибольшее из чисел N_x (ε / 2 )  и  N_y (ε / 2 ) . Тогда
 | x_n  ± y_n  – (a ± b ) |  < ε  при  n > N(ε ) .

То есть мы нашли такую функцию N(ε ) = max (N_x (ε / 2 ),  N_y (ε / 2 )) , при которой, для любого положительного числа ε > 0 , выполняется неравенство:
(1.1)    | x_n  ± y_n  – (a ± b ) |  < ε  при  n > N(ε ) .
Это и означает, что число a ± b является пределом последовательности {x_n  ± y_n } .
Свойство доказано.

Теорема о пределе произведения числовых последовательностей

Все свойства Пусть существуют конечные пределы
lim_{n → ∞} x_n  = a  и  lim_{n → ∞} y_n  = b числовых последовательностей {x_n } и {y_n } .
Тогда существует предел произведения последовательностей {x_n· y_n} , и он равен произведению их пределов:
lim_{n → ∞} (x_n  ⋅ y_n ) = lim_{n → ∞} x_n  ⋅ lim_{n → ∞} y_n  = a ⋅ b .

Для доказательства свойства произведения (2), нам нужно найти такую функцию N(ε ) , при которой, для любого положительного числа ε > 0 , выполняется неравенство
(2.1)    | x_n  ⋅ y_n  – a ⋅ b |  < ε  при  n > N(ε ) .
При этом мы имеем функции N_x (ε₁ ) и N_y (ε₂ ) , при которых, для любых положительных ε₁ и ε₂ , выполняются неравенства (5) и (6):
(5)    | x_n  – a |  < ε₁  при  n > N_x (ε₁ ) ;
(6)    | y_n  – b |  < ε₂  при  n > N_y (ε₂ ) .

Преобразуем модуль разности в (2.1), применяя свойства неравенств:
 | x_n  ⋅ y_n  – a ⋅ b |  =  | x_n  ⋅ y_n  – ay_n  + ay_n  – a ⋅ b |  =
  | (x_n  – a ) ⋅ y_n  + a ⋅ (y_n  – b ) |  ≤  | (x_n  – a ) |  ⋅  | y_n  |  +  | a |  ⋅  | y_n  – b |  |  .
Поскольку последовательность {y_n } имеет конечный предел, то она ограничена некоторым положительным числом M_y :  | y_n  |  ≤ M_y (см. Основные свойства пределов последовательностей). Применим (5) и (6). Тогда
 | x_n  ⋅ y_n  – a ⋅ b |  ≤  | (x_n  – a ) |  ⋅  | y_n  |  +  | a |  ⋅  | y_n  – b |  |  < ε₁  ⋅ M_y  +  | a |  ⋅ ε₂ .
Положим ε₁  = ε2M_y ;  ε₂  = ε2 | a |  . Тогда при n > N_x (ε / (2M_y ))  и  n > N_y (ε / (2 | a | )) ,
 | x_n  ⋅ y_n  – a ⋅ b |  < ε .
Пусть, при заданном ε ,  N(ε ) есть наибольшее из чисел N_x (ε / (2M_y ))  и  N_y (ε / (2 | a | )) . Тогда
 | x_n  ⋅ y_n  – a ⋅ b |  < ε  при  n > N(ε ) .

То есть мы нашли такую функцию N(ε ) = max (N_x (ε / (2M_y )),  N_y (ε / (2 | a | ))) , при которой, для любого положительного числа ε > 0 , выполняется неравенство:
(2.1)    | x_n  ⋅ y_n  – a ⋅ b |  < ε  при  n > N(ε ) .
Это и означает, что число  a ⋅ b  является пределом последовательности {x_n  ⋅ y_n } .
Свойство доказано.

Теорема о вынесении постоянной за знак предела

Все свойства Пусть существует конечный предел
lim_{n → ∞} x_n  = a  числовой последовательности {x_n } .
И пусть последовательность {Cx_n } образована из {x_n } , умножением ее на постоянное число C .
Тогда постоянную C можно выносить за знак предела:
lim_{n → ∞} (C ⋅ x_n ) = C ⋅ lim_{n → ∞} x_n  = C ⋅ a .

Это свойство является следствием свойства произведения последовательностей. Для доказательства рассмотрим последовательность, все элементы которой равны числу C : y_n  = C . Предел этой последовательности равен этому числу:
lim_{n → ∞} y_n  = C
(см. Основные свойства пределов последовательностей).

Применим свойство произведения последовательностей:
lim_{n → ∞} (C ⋅ x_n ) = lim_{n → ∞} (y_n  ⋅ x_n ) = lim_{n → ∞} y_n  ⋅ lim_{n → ∞} x_n  = C ⋅ a .
Свойство доказано.

Теорема о пределе частного числовых последовательностей

Все свойства Пусть существуют конечные пределы
lim_{n → ∞} x_n  = a  и  lim_{n → ∞} y_n  = b числовых последовательностей {x_n } и {y_n } .
Причем b ≠ 0  и  y_n  ≠ 0  для всех n .
Тогда существует предел частного последовательностей {x_n / y} , и он равен частному их пределов:
lim_{n → ∞} x_ny_n = lim_{n → ∞} x_nlim_{n → ∞} y_n = ab .

Для доказательства свойства частного (3), нам нужно найти такую функцию N(ε ) , при которой, для любого положительного ε > 0 , выполняется неравенство:
(3.1)   | x_ny_n – ab  | < ε  при  n > N(ε ) .
При этом мы имеем функции N_x (ε₁ ) и N_y (ε₂ ) , при которых, для любых положительных ε₁ и ε₂ , выполняются неравенства (5) и (6):
(5)    | x_n  – a |  < ε₁  при  n > N_x (ε₁ ) ;
(6)    | y_n  – b |  < ε₂  при  n > N_y (ε₂ ) .

Преобразуем модуль разности в (3.1), применяя свойства неравенств:
| x_ny_n – ab  | = | x_n b – y_n ay_n b  | = | x_n b – ab + ab – y_n ay_n b  | =
 | (x_n  – a )b – a(y_n  – b )y_n b  | ≤  | x_n  – a |  | y_n  |  +  | y_n  – b |  | a |  | y_n  |  | b |  .
Тем самым мы получили следующую оценку:
(3.2)   | x_ny_n – ab  | ≤  | x_n  – a |  | y_n  |  +  | y_n  – b |  | a |  | y_n  |  | b |  .

Сделаем оценку для  | y_n  |  . Подставим в (6) ε₂  =  | b |  / 2 :
 | y_n  – b |  <  | b |  / 2  при  n > N_y ( | b |  / 2 ) .
Заметим, что  | y_n  – b |  есть расстояние между точками y_n и b на числовой прямой. Поскольку расстояние между точками 0 и b равно  | b |  а расстояние между точками y_n и b меньше  | b |  / 2 :  | y_n  – b |  <  | b |  / 2 , то расстояние между точками y_n и 0 больше  | b |  / 2 :
 | y_n  – 0 |  >  | b |  / 2 , или
 | y_n  |  >  | b |  / 2 .
Это неравенство можно получить и другим способом. Применяя свойства неравенств и соотношение  | y_n  – b |  <  | b |  / 2 имеем:
 | b |  =  |  – b |  =  | y_n  – b – y_n  |  ≤  | y_n  – b |  +  | y_n  |  <  | b |  / 2 +  | y_n  |  ;
 | b |  <  | b |  / 2 +  | y_n  |  ;
 | b |  / 2 <  | y_n  |  .
Итак, мы нашли, что
 | y_n  |  >  | b |  / 2  при  n > N₁ ,
где N₁  = N_y ( | b |  / 2 ) . Тогда
(3.3)   1 | y_n  |  < 2 | b |   при  n > N₁ .

Подставим (5), (6) и (3.3) в (3.2):
| x_ny_n – ab  | ≤  | x_n  – a |  | y_n  |  +  | y_n  – b |  | a |  | y_n  |  | b |  < 2ε₁ | b |  + 2ε₂  | a | b² .
Это неравенство выполняется при одновременном выполнении трех неравенств:
n > N₁ ;  n > N_x (ε₁ );  n > N_y (ε₂ ) .
Подставим ε₁  =  | b | 4 ε ,   ε₂  = b²4 | a |  ε . И пусть N(ε ) обозначает максимальное из чисел N₁ ,  N_x (  | b | 4 ε  ),  N_y ( b²4 | a |  ε  ) . Тогда
| x_ny_n – ab  | < 2ε₁ | b |  + 2ε₂  | a | b² = ε2 + ε2 = ε;  n > N(ε ) .

То есть мы нашли такую функцию
N(ε ) = max (N_y ( | b |  / 2 ),  N_x (  | b | 4 ε  ),  N_y ( b²4 | a |  ε  )) ,
при которой, для любого положительного ε > 0 , выполняется неравенство
(3.1)   | x_ny_n – ab  | < ε  при  n > N(ε ) .
Это и означает, что число a/b является пределом последовательности { x_ny_n  } .
Свойство доказано.

Теорема о пределе абсолютного значения элементов последовательности

Все свойства Пусть существует конечный предел
lim_{n → ∞} x_n  = a  числовой последовательности {x_n } .
И пусть последовательность { | x_n  | } составлена из элементов x_n , взятых по абсолютной величине.
Тогда
lim_{n → ∞}  | x_n  |  =  | a |  .

Для доказательства этого свойства, нам нужно найти такую функцию N(ε ) , при которой, для любого положительного ε > 0 , выполняется неравенство:
| | x_n  |  –  | a | | < ε  при  n > N(ε ) .
При этом у нас есть функция N_x (ε ) , при которой выполняется неравенство (5):
(5)    | x_n  – a |  < ε  при  n > N_x (ε ) .

Воспользуемся известным неравенством:
| | A |  –  | B | | ≤ |A – B  |
и применим (5):
| | x_n  |  –  | a | | ≤  | x_n  – a |  < ε; .
Последнее выполняется при n > N_x (ε ) .
То есть мы можем взять N(ε ) = N_x (ε ) .

Итак, для любого ε > 0 ,
| | x_n  |  –  | a | | < ε  при  n > N_x (ε ) .
Свойство доказано.