Доказательство формулы производной сложной функции
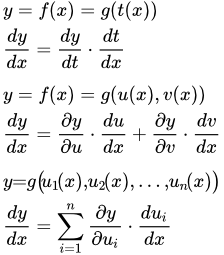
Основные формулы
Здесь мы приводим вывод следующих формул для производной сложной функции.
Пусть функцию y = f (x) можно представить как композицию двух функций y = g(t) и t = t(x): y = g(t(x)). Тогда
f ′(x) = g ′(t) ⋅ t ′(x).
Если y = f (x) = g(u(x), v(x)), то
f ′(x) = g ′u(u, v) ⋅ u ′(x) + g ′v(u, v) ⋅ v ′(x).
Если y = f (x) = g(u1 (x), u2 (x), . . ., un (x)), то
f ′(x) = nΣi = 1 g ′ui(u1, u2, ... un) ⋅ duidx.
В другой системе обозначений приведенные выше формулы можно записать так.
dydx = dydt ⋅ dtdx,
dydx = ∂y∂u ⋅ dudx + ∂y∂v ⋅ dvdx,
dydx = nΣi = 1 ∂y∂ui ⋅ duidx.
Теорема. Производная сложной функции от одной переменной
Пусть функция t = t(x) имеет производную при некотором значении переменной x = x0, а функция y = g(t) имеет производную при значении переменной t0 = t(x0).Тогда сложная (составная) функция y = f (x) = g(t(x)) имеет производную в точке x0, которая определяется по формуле:
(1.1) f ′(x0) = g ′(t0) ⋅ t ′(x0).
Формулу (1.1) также можно записать так:
dydx = dydt ⋅ dtdx;
dydx = dgdt ⋅ dtdx.
Доказательство
Выберем значение x0, удовлетворяющее условию теоремы. Далее считаем, что x0 фиксировано. То есть все последующие выкладки будем выполнять при одном и том же значении x0. Тогда t0 = t(x0) тоже будет фиксировано.
Покажем, что существует такая окрестность точки x0, в которой определена сложная функция f (x) = g(t(x)).
Поскольку существует производная g ′(t0), то функция g(t) определена в некоторой окрестности U(t0, εt) точки t0, то есть при
| Δt | < εt,
где Δt = t – t0.
Поскольку существует производная t ′(x0), то функция t(x) определена в некоторой окрестности точки x0. Также она дифференцируема в x0 и, согласно свойству дифференцируемых функций, непрерывна в x0:
(1.2) limΔx → 0 Δt = 0,
где Δt = t(x0 + Δx) – t(x0).
Согласно определению предела, из (1.2) следует, что существует такая окрестность U(x0, δx) точки x0, принадлежащая области определения t(x), в которой
(1.3) | Δt | < εt при | Δx | < δx,
где Δx = x – x0.
А поскольку при | Δt | < εt функция g(t) определена, то сложная функция g(t(x)) определена в окрестности U(x0, δx) точки x0, то есть при | Δx | < δx.
Теперь покажем, что f ′(x0) = g ′(t0) ⋅ t ′(x0).
Поскольку существуют производные g ′(t0) и t ′(x0), то функции g и t дифференцируемы в точках t0 и x0, соответственно. По определению дифференцируемой функции,
(1.4) Δg = g ′(t0) ⋅ Δt + αg (Δt) ⋅ Δt,
(1.5) Δt = t ′(x0) ⋅ Δx + αt (Δx) ⋅ Δx,
где αg (Δt) и αt (Δx) – бесконечно малые функции:
(1.6) limΔt → 0 αg (Δt) = 0;
(1.7) limΔx → 0 αt (Δx) = 0.
Подставим (1.5) в (1.4).
(1.8) Δg = g ′(t0) ⋅ t ′(x0) ⋅ Δx + g ′(t0) ⋅ αt (Δx) ⋅ Δx + αg (Δt) ⋅ Δt.
Находим производную f ′(x0). Для этого сначала преобразуем отношение Δ f / Δx.
Δ f = f (x0 + Δx) – f (x0) = g(t(x0 + Δx)) – g(t(x0)) =
g (t(x0) + t(x0 + Δx) – t(x0)) – g(t0) = g(t0 + Δt) – g(t0) = Δg.
Используем (1.8).
Δ f Δx = ΔgΔx = g ′(t0) ⋅ t ′(x0) + g ′(t0) ⋅ αt (Δx) + αg (Δt) ⋅ ΔtΔx.
Теперь находим предел при Δx → 0.
f ′(x0) = limΔx → 0 Δ f Δx =
g ′(t0) ⋅ t ′(x0) + g ′(t0) ⋅ limΔx → 0 αt (Δx) + limΔx → 0(αg (Δt)) ⋅ limΔx → 0 ΔtΔx =
g ′(t0) ⋅ t ′(x0) + g ′(t0) ⋅ 0 + limΔx → 0(αg (Δt)) ⋅ t ′(x0);
(1.9) f ′(x0) = g ′(t0) ⋅ t ′(x0) + t ′(x0) ⋅ limΔx → 0 αg (Δt).
Здесь мы применили (1.7) и свойства пределов суммы и произведения учитывая, что limΔx → 0 ΔtΔx = t ′(x0).
В силу непрерывности функции t(x) в точке x0, Δt → 0 при Δx → 0. Делая замену переменной в оставшемся пределе и применяя (1.6), находим.
limΔx → 0 αg (Δt) ≡ limΔx → 0 αg (Δt(Δx)) = limΔt → 0 αg (Δt) = 0.
С учетом этого, из (1.9) находим:
f ′(x0) = g ′(t0) ⋅ t ′(x0).
Формула (1.1) доказана.
Следствие
Если функцию y = f (x) от переменной x можно представить как сложную функцию от сложной функции
f (x) = g(u(v(x))),
то ее производная определяется по формуле:
(С.1) f ′(x) = g ′(u) ⋅ u ′(v) ⋅ v ′(x).
Здесь v(x), u(v) и g(u) есть некоторые дифференцируемые функции в точках x, v = v(x), u = u(x), соответственно.
Эту формулу можно записать так:
dydx = dydu ⋅ dudv ⋅ dvdx.
Чтобы доказать (С.1), мы последовательно вычисляем производную по правилу дифференцирования сложной функции.
Рассмотрим сложную функцию
z(x) = u(v(x)).
Ее производная
z ′(x) = u ′(v) ⋅ v ′(x).
Рассмотрим исходную функцию
f (x) = g(z(x)).
Ее производная
f ′(x) = g ′(z) ⋅ z ′(x) = g ′(z) ⋅ u ′(v) ⋅ v ′(x) = g ′(u) ⋅ u ′(v) ⋅ v ′(x).
Производная сложной функции от двух переменных
Теперь пусть сложная функция зависит от нескольких переменных. Вначале рассмотрим случай сложной функции от двух переменных.
Тогда сложная функция y = f (x) = g(u(x), v(x)) имеет производную в точке x0, которая определяется по формуле:
(2.1) f ′(x0) = g ′u(u0, v0) ⋅ u ′(x0) + g ′v(u0, v0) ⋅ v ′(x0).
Формулу (2.1) можно записать так:
dydx = ∂y∂u ⋅ dudx + ∂y∂v ⋅ dvdx.
Доказательство
Покажем, что существует такая окрестность точки x0, в которой определена сложная функция f (x) = g(u(x), v(x)).
Поскольку функция g ′(u, v) дифференцируема в точке (u0, v0), то она определена в некоторой окрестности этой точки. Обрежем эту окрестность так, чтобы она имела форму квадрата со стороной 2εuv. То есть считаем, что g(u, v) определена в окрестности U(u0, v0, εuv) точки (u0, v0), которая дается неравенствами
(2.2) | u – u0 | < εuv;
(2.3) | v – v0 | < εuv.
Поскольку существует производная u ′(x0), то функция u(x) определена в некоторой окрестности точки x0. Также она дифференцируема в x0 и, согласно свойству дифференцируемых функций, непрерывна в x0:
(2.4) limΔx → 0 Δu = 0,
где Δu = u(x0 + Δx) – u(x0).
Согласно определению предела, из (2.4) следует, что существует такая окрестность U(x0, δux) точки x0, принадлежащая области определения u(x), в которой
(2.5) | Δu | < εuv при | Δx | < δux.
Рассуждая совершенно аналогичным способом для функции v(x) приходим к выводу, что существует такая окрестность U(x0, δvx) точки x0, принадлежащая области определения v(x), в которой
(2.6) | Δv | < εuv при | Δx | < δvx.
Возьмем δx = min(δux, δvx). На основании (2.5) и (2.6) имеем:
| Δu | < εuv и | Δv | < εuv при | Δx | < δx.
То есть выполняются неравенства (2.2) и (2.3). Это означает, что при | Δx | < δx определена сложная функция g(u(x), v(x)).
Теперь покажем, что f ′(x0) = g ′u(u0, v0) ⋅ u ′(x0) + g ′v(u0, v0) ⋅ v ′(x0).
Поскольку существуют производные u ′(x0) и v ′(x0), то функции u и v дифференцируемы в точке x0. По определению дифференцируемой функции
(2.7) Δu = u ′(x0) ⋅ Δx + αu (Δx) ⋅ Δx,
(2.8) Δv = v ′(x0) ⋅ Δx + αv (Δx) ⋅ Δx,
где αu (Δx) и αv (Δx) – бесконечно малые функции:
(2.9) limΔx → 0 αu (Δx) = 0;
(2.10) limΔx → 0 αv (Δx) = 0.
По условию теоремы g(u, v) дифференцируема в точке u0 = u(x0), v0 = v(x0). Тогда ее приращение в этой точке можно представить в следующем виде.
(2.11) Δg = g ′u ⋅ Δu + g ′v ⋅ Δv + ε1 (Δu, Δv) ⋅ Δu + ε2 (Δu, Δv) ⋅ Δv, где
(2.12) limΔu → 0Δv → 0 ε1 (Δu, Δv) = 0; limΔu → 0Δv → 0 ε2 (Δu, Δv) = 0.
Здесь мы для краткости отбросили аргументы производных: g ′u = g ′u(u0, v0), g ′v = g ′v(u0, v0).
Подставим (2.7), (2.8) в (2.11).
(2.13) Δg = g ′u ⋅ u ′ ⋅ Δx + g ′v ⋅ v ′ ⋅ Δx + g ′u ⋅ αu (Δx) ⋅ Δx + g ′v ⋅ αv (Δx) ⋅ Δx +
ε1 (Δu, Δv) ⋅ Δu + ε2 (Δu, Δv) ⋅ Δv.
Здесь также u ′ = u ′(x0), v ′ = v ′(x0).
Находим производную f ′(x0). Для этого сначала преобразуем отношение Δ f / Δx.
Δ f = f (x0 + Δx) – f (x0) = g (u(x0 + Δx), v(x0 + Δx)) – g(u(x0), v(x0)) =
g (u(x0) + u(x0 + Δx) – u(x0), v(x0) + v(x0 + Δx) – v(x0)) – g(u(x0), v(x0)) =
g(u0 + Δu, v0 + Δv) – g(u0, v0) = Δg.
Используем (2.13).
Δ f Δx = ΔgΔx = g ′u ⋅ u ′ + g ′v ⋅ v ′ + g ′u ⋅ αu (Δx) + g ′v ⋅ αv (Δx) +
ε1 (Δu, Δv) ⋅ ΔuΔx + ε2 (Δu, Δv) ⋅ ΔvΔx.
Теперь находим предел при Δx → 0.
f ′ = limΔx → 0 Δ f Δx = g ′u ⋅ u ′ + g ′v ⋅ v ′ + g ′u ⋅ limΔx → 0 αu (Δx) + g ′v ⋅ limΔx → 0 αv (Δx) +
limΔx → 0(ε1 (Δu, Δv)) ⋅ limΔx → 0 ΔuΔx + limΔx → 0(ε2 (Δu, Δv)) ⋅ limΔx → 0 ΔvΔx =
g ′u ⋅ u ′ + g ′v ⋅ v ′ + g ′u ⋅ 0 + g ′v ⋅ 0 + limΔx → 0(ε1 (Δu, Δv)) ⋅ u ′ + limΔx → 0(ε2 (Δu, Δv)) ⋅ v ′;
(2.14) f ′ = g ′u ⋅ u ′ + g ′v ⋅ v ′ + u ′ ⋅ limΔx → 0 ε1 (Δu, Δv) + v ′ ⋅ limΔx → 0 ε2 (Δu, Δv).
Здесь мы применили (2.9), (2.10) и свойства пределов суммы и произведения учитывая, что limΔx → 0 ΔuΔx = u ′, limΔx → 0 ΔvΔx = v ′.
В силу непрерывности функций u(x) и v(x) в точке x0, Δu → 0 и Δv → 0 при Δx → 0. Делая замену переменной в оставшемся пределе и применяя (2.12), находим.
limΔx → 0 ε1 (Δu, Δv) = 0, limΔx → 0 ε2 (Δu, Δv) = 0.
С учетом этого, из (2.14) находим:
f ′ = g ′u ⋅ u ′ + g ′v ⋅ v ′.
Формула (2.1) доказана.
Производная сложной функции от нескольких переменных
Приведенный выше вывод легко обобщается на случай, когда число переменных сложной функции больше двух.
Например, если g является функцией от трех переменных, то
y = f (x) = g(u(x), v(x), w(x)),
где
u(x), v(x) и w(x) есть дифференцируемые функции при некотором значении переменной x;
g(u, v, w) – дифференцируемая функция, от трех переменных, в точке u = u(x), v = v(x), w = w(x).
Тогда, из дифференцируемости функции g, имеем:
(3.1) Δg = g ′u Δu + g ′v Δv + g ′w Δw + ε1 (Δu, Δv, Δw) Δu + ε2 (Δu, Δv, Δw) Δv +
ε3 (Δu, Δv, Δw) Δw,
где
limΔu → 0Δv → 0Δw → 0 ε1 (Δu, Δv, Δw) = 0; limΔu → 0Δv → 0Δw → 0 ε2 (Δu, Δv, Δw) = 0; limΔu → 0Δv → 0Δw → 0 ε3 (Δu, Δv, Δw) = 0.
В силу непрерывности u(x), v(x), w(x),
limΔx → 0 Δu = 0; limΔx → 0 Δv = 0; limΔx → 0 Δw = 0.
Тогда
limΔx → 0 ε1 (Δu, Δv, Δw) = limΔu → 0Δv → 0Δw → 0 ε1 (Δu, Δv, Δw) = 0;
limΔx → 0 ε2 (Δu, Δv, Δw) = limΔu → 0Δv → 0Δw → 0 ε2 (Δu, Δv, Δw) = 0;
limΔx → 0 ε1 (Δu, Δv, Δw) = limΔu → 0Δv → 0Δw → 0 ε1 (Δu, Δv, Δw) = 0.
Разделив (3.1) на Δx и выполнив предельный переход Δx → 0, получим:
df dx = ∂g(u, v, w)∂u dudx + ∂g(u, v, w)∂v dvdx + ∂g(u, v, w)∂w dwdx.
Или
dydx = ∂y∂u dudx + ∂y∂v dvdx + ∂y∂w dwdx.
И, наконец, рассмотрим самый общий случай.
Пусть функцию y = f (x) от переменной x можно представить как сложную функцию от n переменных в следующем виде:
y = f (x) = g(u1 (x), u2 (x), ... un (x)),
где
ui (x) есть дифференцируемые функции при некотором значении переменной x;
g(u1, u2, ... un) – дифференцируемая функция от n переменных в точке
u1 = u1 (x), u2 = u2 (x), . . ., un = un (x).
Тогда
df dx = nΣi = 1 ∂g(u1, u2, ... un)∂ui duidx.
Или
dydx = nΣi = 1 ∂y∂ui duidx.
Автор: Олег Одинцов. Опубликовано: Изменено: