Все картинки раздела «Динамика твердого тела и системы»
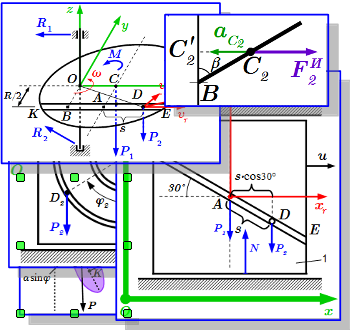
Здесь собраны все изображения раздела «Динамика твердого тела и системы» теоретической механики. Просматривая их можно быстро найти интересующий материал и перейти на страницу с его изложением.
Содержание
См. также:
Все понятия, определения и теоремы динамики твердого тела и системы (обзорная страница)
Динамика твердого тела и системы. Все определения, законы и теоремы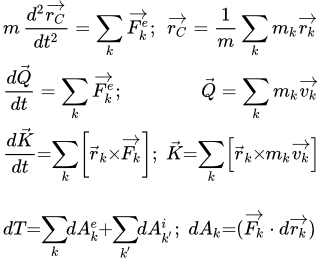
Все понятия, определения, законы, теоремы и свойства динамики твердого тела и системы. Общие теоремы динамики системы. Теоремы о движении центра масс, об изменении количества движения, об изменении главного момента количества движения, об изменении кинетической энергии. Принципы Даламбера, и возможных перемещений. Общее уравнение динамики. Уравнения Лагранжа. 
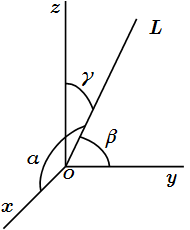Ось OL составляет углы α, β, γ с осями x, y, z. 
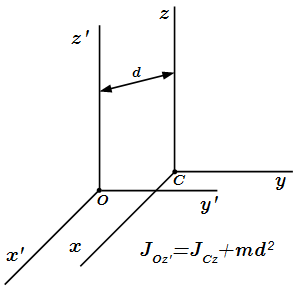Теорема Гюйгенса-Штейнера 
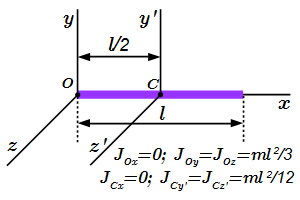Момент инерции однородного стержня. 
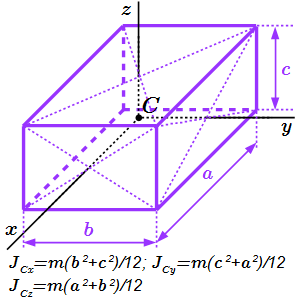Момент инерции прямоугольного параллелепипеда 
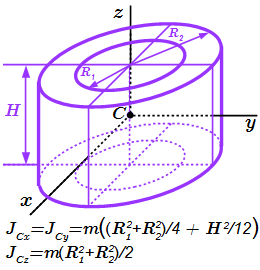Момент инерции полого цилиндра 
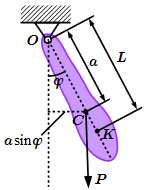Физический маятник. 
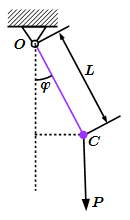Математический маятник.
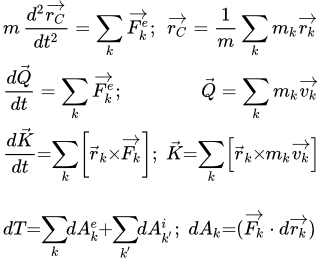Все понятия, определения, законы, теоремы и свойства динамики твердого тела и системы. Общие теоремы динамики системы. Теоремы о движении центра масс, об изменении количества движения, об изменении главного момента количества движения, об изменении кинетической энергии. Принципы Даламбера, и возможных перемещений. Общее уравнение динамики. Уравнения Лагранжа. 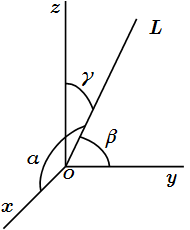Ось OL составляет углы α, β, γ с осями x, y, z. 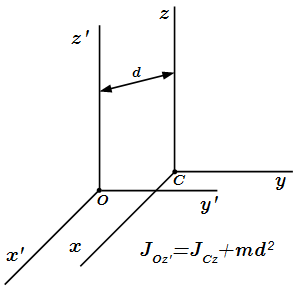Теорема Гюйгенса-Штейнера 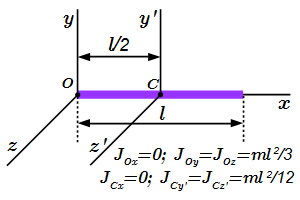Момент инерции однородного стержня. Момент инерции прямоугольного параллелепипеда Момент инерции полого цилиндра Физический маятник. Математический маятник. Другие страницы
Понятие механических связей и их классификация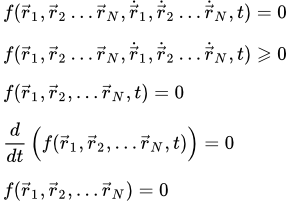
Дается определение понятия механических связей, и излагаются физические принципы их возникновения. Даны определения основных видов связей, применяемых в теоретической механике, и приводится их классификация. Рассмотрены примеры связей различных типов. 
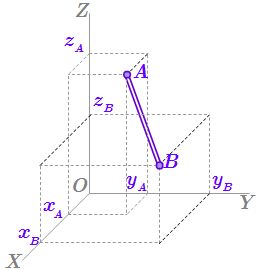Связь – жесткий стержень 
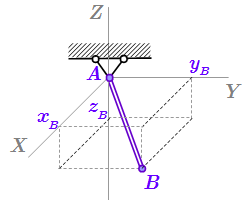Связь – закрепленный на одном конце абсолютно жесткий стержень 
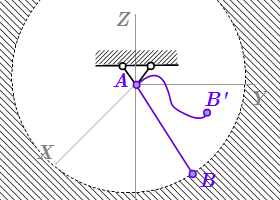Связь – нерастяжимая нить 
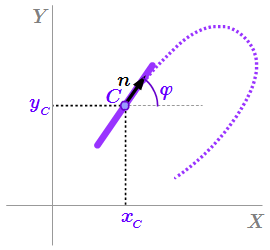Связь – лезвие конька 
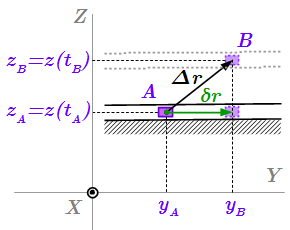Возможное Δr и виртуальное δr перемещения Теорема о движении центра масс системы. Решение задач
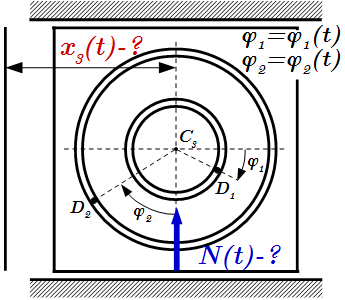Приводятся формулы и законы, применяемые при решении задач с помощью теоремы о движении центра масс системы. Рассмотрены примеры решения задач. В одной задаче требуется найти смещение плиты с движущимися по ней грузами и реакцию направляющих. В другой задаче нужно найти вертикальную составляющую реакции в точке крепления кривошипно-шатунного механизма с ползуном. 
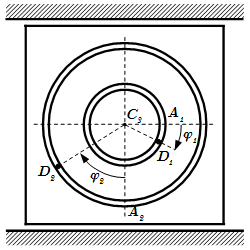Условие задачи. Плита с движущимися грузами. 
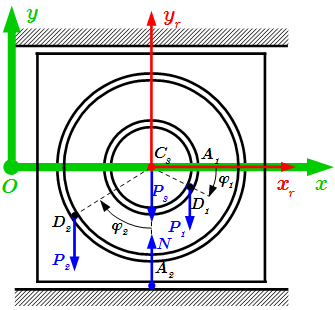Неподвижная и подвижная системы координат, связанная с плитой 
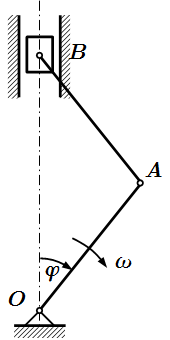Условие задачи. Кривошипно-шатунный механизм. 
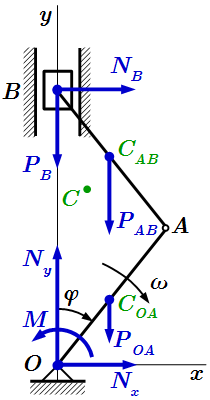Внешние силы, действующие на систему 
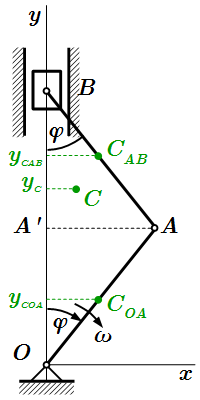Центры масс шатуна, кривошипа и ползуна. Решение задач на применение теоремы об изменении количества движения системы
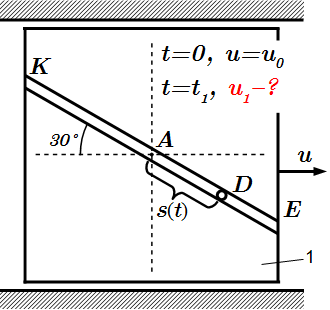Приводится инструкция, как решать задачи на применение теоремы об изменении количества движения системы. Рассмотрен пример решения задачи. 
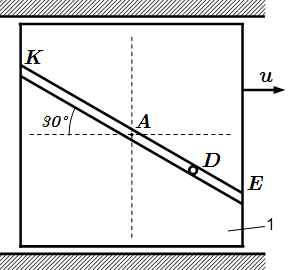Условие задачи. Плита 1 с движущимся грузом D. 
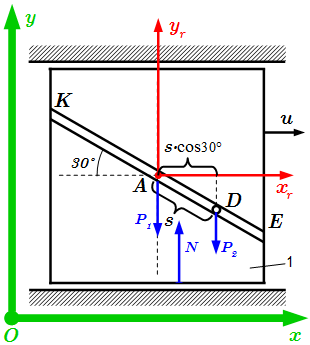Рисунок к решению задачи. 
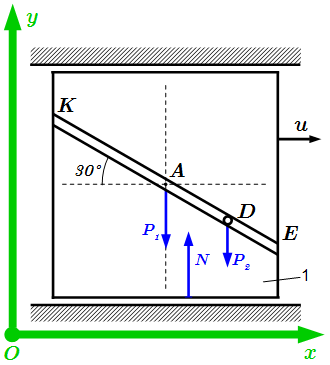Внешние силы, действующие на систему. 
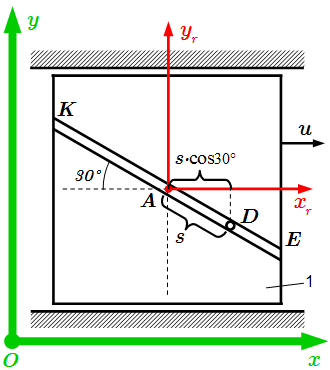Неподвижная Oxy и подвижная Axryr системы координат. Решение задач на применение теоремы об изменении кинетического момента системы
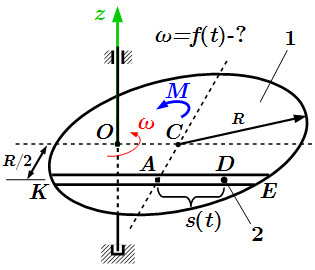Инструкция о порядке решения задач на применение теоремы об изменении кинетического момента системы. Рассмотрены примеры решения задач с краткими и подробными решениями. 
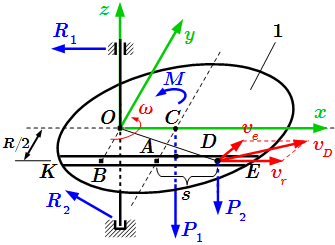Внешние силы, действующие на систему. 
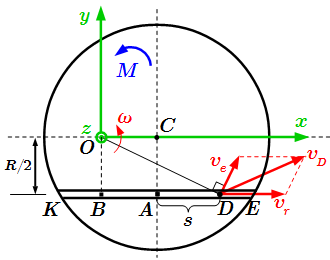Плита и груз. Вид сверху. 
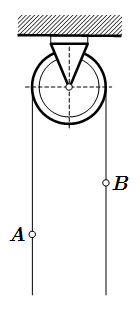Канат, перекинутый через блок, с движущимся по нему человеком A и прикрепленным грузом B. 
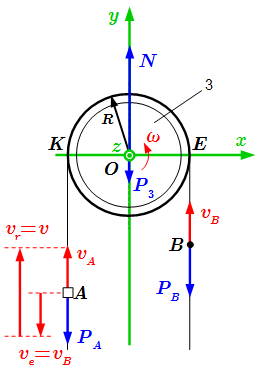Внешние силы; сложное движение точки A. Теорема об изменении кинетической энергии. Пример решения задачи.
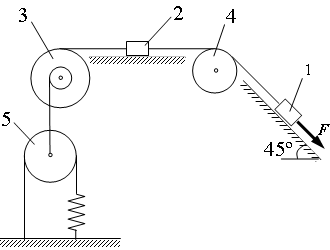Пример решения задачи с применением теоремы об изменении кинетической энергии системы с твердыми телами, блоками, шкивами и пружиной. 
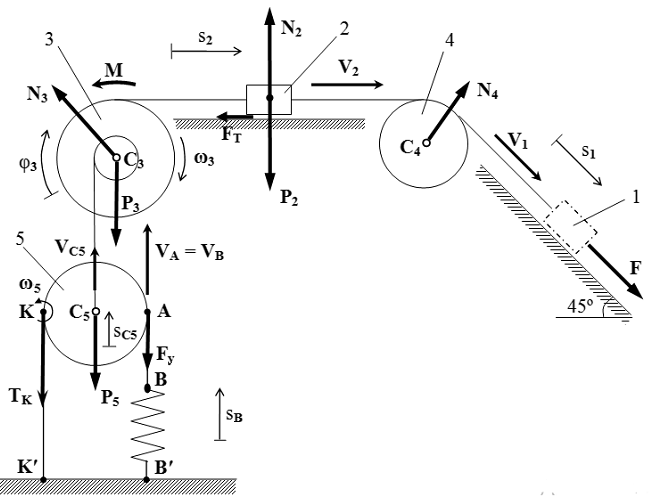Расчетная схема задачи. 
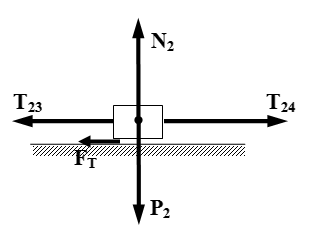Силы, действующие на тело 2. Общее уравнение динамики. Пример решения задачи
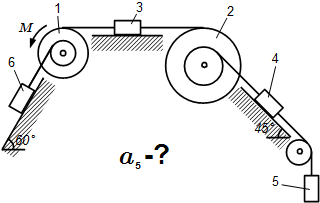Пример решения задачи с применением общего уравнения динамики (принцип Даламбера – Лагранжа) для системы с твердыми телами, грузами, шкивами и блоком, соединенных нитями. 
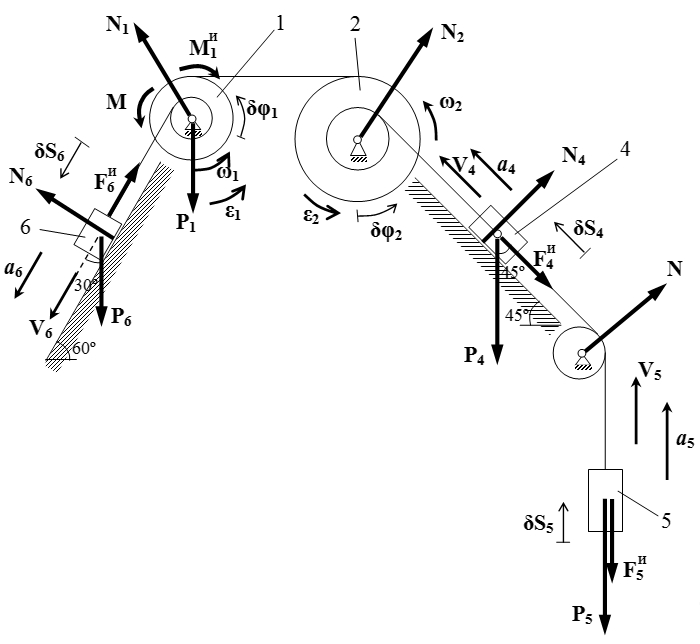Расчетная система сил Принцип Даламбера (кинетостатика). Решение задачи
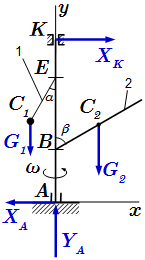Рассмотрены законы, применяемые при решении задач методом кинетостатики. Приводится пример решения задачи, используя принцип Даламбера на определение реакций опор вращающегося вала. Приводится решение задачи двумя способами – применяя принцип Даламбера к стержню как к системе материальных точек, и как к твердому телу. 
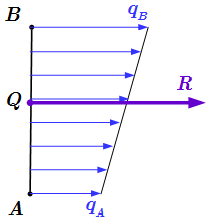Линейно распределенная нагрузка и ее равнодействующая. 
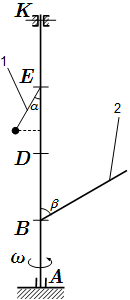Рисунок к условию задачи. 
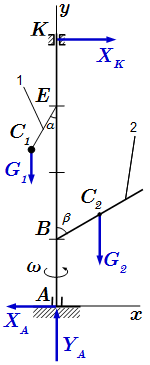Внешние силы, действующие на вал. 
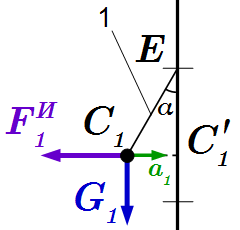Сила инерции груза, рассматриваемого как материальная точка. 
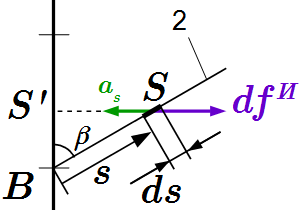Сила инерции элемента стержня 
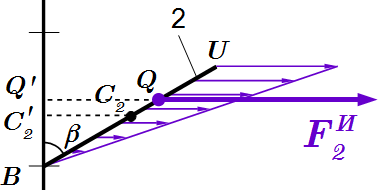Эпюра сил инерции стержня и равнодействующая. 
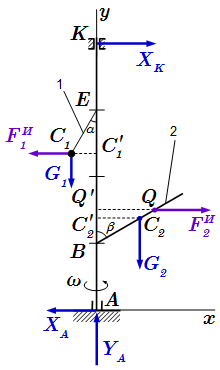Задача кинетостатики на равновесие системы сил. 
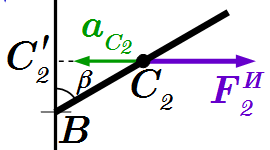Главный вектор инерции стержня, приведенный к центру масс. 
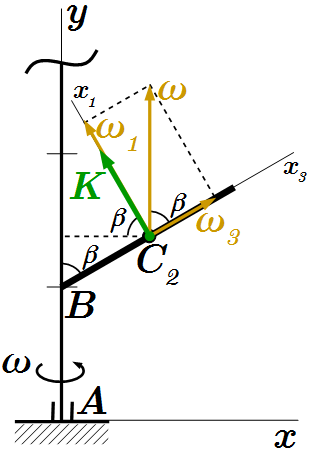Момент количества движения стержня 
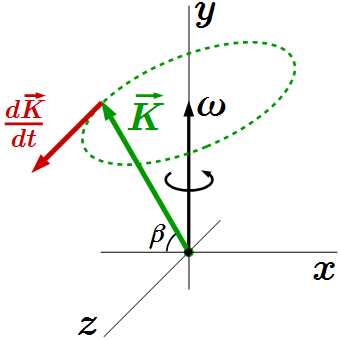Производная по времени момента количества движения стержня 
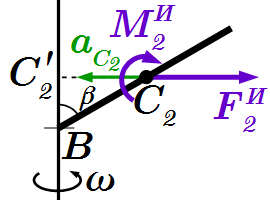Силы инерции стержня, приведенные к центру масс. 
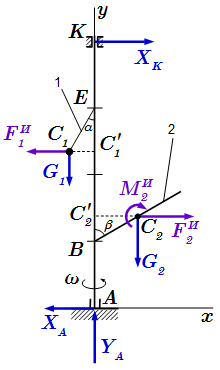Задача кинетостатики на равновесие системы сил. Общий способ.
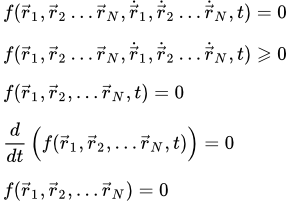Дается определение понятия механических связей, и излагаются физические принципы их возникновения. Даны определения основных видов связей, применяемых в теоретической механике, и приводится их классификация. Рассмотрены примеры связей различных типов. Связь – жесткий стержень Связь – закрепленный на одном конце абсолютно жесткий стержень Связь – нерастяжимая нить Связь – лезвие конька Возможное Δr и виртуальное δr перемещения Теорема о движении центра масс системы. Решение задачПриводятся формулы и законы, применяемые при решении задач с помощью теоремы о движении центра масс системы. Рассмотрены примеры решения задач. В одной задаче требуется найти смещение плиты с движущимися по ней грузами и реакцию направляющих. В другой задаче нужно найти вертикальную составляющую реакции в точке крепления кривошипно-шатунного механизма с ползуном. Условие задачи. Плита с движущимися грузами. Неподвижная и подвижная системы координат, связанная с плитой Условие задачи. Кривошипно-шатунный механизм. Внешние силы, действующие на систему Центры масс шатуна, кривошипа и ползуна. Решение задач на применение теоремы об изменении количества движения системыПриводится инструкция, как решать задачи на применение теоремы об изменении количества движения системы. Рассмотрен пример решения задачи. Условие задачи. Плита 1 с движущимся грузом D. Рисунок к решению задачи. Внешние силы, действующие на систему. Неподвижная Oxy и подвижная Axryr системы координат. Решение задач на применение теоремы об изменении кинетического момента системыИнструкция о порядке решения задач на применение теоремы об изменении кинетического момента системы. Рассмотрены примеры решения задач с краткими и подробными решениями. Внешние силы, действующие на систему. Плита и груз. Вид сверху. Канат, перекинутый через блок, с движущимся по нему человеком A и прикрепленным грузом B. Внешние силы; сложное движение точки A. Теорема об изменении кинетической энергии. Пример решения задачи.Пример решения задачи с применением теоремы об изменении кинетической энергии системы с твердыми телами, блоками, шкивами и пружиной. Расчетная схема задачи. Силы, действующие на тело 2. Общее уравнение динамики. Пример решения задачиПример решения задачи с применением общего уравнения динамики (принцип Даламбера – Лагранжа) для системы с твердыми телами, грузами, шкивами и блоком, соединенных нитями. Расчетная система сил Принцип Даламбера (кинетостатика). Решение задачиРассмотрены законы, применяемые при решении задач методом кинетостатики. Приводится пример решения задачи, используя принцип Даламбера на определение реакций опор вращающегося вала. Приводится решение задачи двумя способами – применяя принцип Даламбера к стержню как к системе материальных точек, и как к твердому телу. Линейно распределенная нагрузка и ее равнодействующая. Рисунок к условию задачи. Внешние силы, действующие на вал. Сила инерции груза, рассматриваемого как материальная точка. Сила инерции элемента стержня Эпюра сил инерции стержня и равнодействующая. Задача кинетостатики на равновесие системы сил. Главный вектор инерции стержня, приведенный к центру масс. Момент количества движения стержня Производная по времени момента количества движения стержня 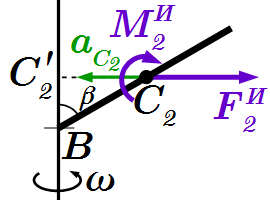Силы инерции стержня, приведенные к центру масс. Задача кинетостатики на равновесие системы сил. Общий способ. ❮ Динамика материальной точки в картинках | Задачи с решениями
См. также: