Теорема Ферма о необходимом условии экстремума функции

Формулировка и доказательство теоремы Ферма о необходимом условии локального экстремума дифференцируемой функции. Геометрический смысл.

Содержание

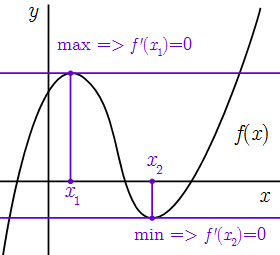
Теорема о необходимом условии экстремума (Ферма)

Если точка

является точкой строгого или нестрогого локального экстремума функции

,
и она дифференцируема в этой точке,
то ее производная в

равна нулю:

Доказательство

Для доказательства применим определение локального экстремума и лемму об односторонних производных

Пусть точка является точкой локального минимума. Тогда существует такая проколотая окрестность этой точки, на которой определена, и
.
Оценим левую производную в . Слева от , . Поэтому
при и .
По свойству пределов функций, связанных неравенством,
.
Но этот предел является левой производной. Отсюда получаем, что левая производная не может быть положительной:
(1) .

Аналогичным образом, справа от , ;
при и .
.
Отсюда получаем, что правая производная не может быть отрицательной:
(2) .

Согласно лемме об односторонних производных, у дифференцируемой функции левая производная равна правой и равна производной:
(3) .
Тогда из (1), (2) и (3) следует, что производная не может быть положительной, и не может быть отрицательной. То есть она может только быть равной нулю:
.

Аналогично, если является точкой локального максимума, то существует такая проколотая окрестность , на которой определена, и
.
Слева от , ;
при и ;
;
.

Справа от , ;
при и ;
;
.
Отсюда
.

Теорема доказана.

Замечания

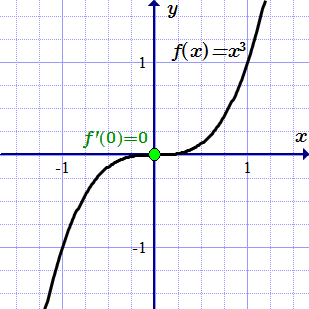
Производная равна нулю, но локального экстремума нет — Производная функции y = x³ при x = 0 равна нулю, но локального экстремума в этой точке нет.

Условие является необходимым условием экстремума, но не достаточным. Например, для функции , , но точка не является локальным экстремумом.

Однако, для нахождения локальных минимумов или максимумов, часто находят корни уравнения . После чего исследуют каждый корень, применяя достаточное условие экстремума. Например условие, чтобы производная меняла знак при переходе через точку , в которой .

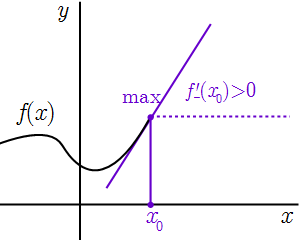
Односторонняя производная слева больше нуля в точке локального максимума — Функция имеет локальный максимум на границе области определения. Она не дифференцируема в этой точке. Поэтому производная слева может быть отличной от нуля.

Если точка находится на границе области определения функции , то в ней может существовать только односторонняя производная. В этом случае не является дифференцируемой в . Поэтому она может иметь в локальный экстремум несмотря на то, что односторонняя производная не равна нулю.

Геометрический смысл

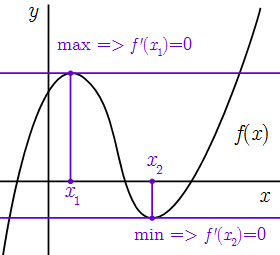
Касательные к графику функции в точках локальных экстремумов параллельны оси x.

Условие означает, что касательная к графику функции , проведенная в точке локального экстремума, параллельна оси абсцисс.

Автор: Олег Одинцов. Опубликовано: 26-05-2024