Основные свойства предела функции
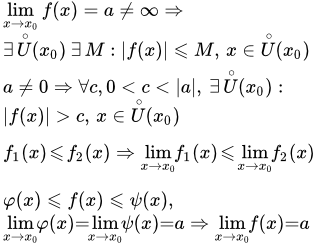
Формулировки свойств
Далее мы считаем, что рассматриваемые функции определены в соответствующей окрестности точки x0. Точка x0 может являться конечным числом или одним из символов бесконечности: . Окрестность может быть как двусторонней для двусторонних пределов, так и односторонней для односторонних.
то это изменение никак не повлияет на существование и величину предела функции в произвольной точке x0.
Доказательство
то существует такая проколотая окрестность точки x0, в которой функция f(x) ограничена:
.
Доказательство
.
Тогда, для любого числа c из интервала , существует такая проколотая окрестность точки x0, что для всех x, принадлежащих этой окрестности: ,
, если ;
, если .
Доказательство
то .
Доказательство
она имеет в этой точке равные односторонние пределы.
Доказательство
,
то .
Доказательство
Заметим, что если функции удовлетворяют строгому неравенству , то их пределы все равно связаны нестрогим неравенством .
,
то .
Доказательство
В частности, если в некоторой проколотой окрестности точки
,
то если , то и ;
если , то и .
,
и существуют конечные (или бесконечные определенного знака) равные пределы:
,
то существует предел функции :
.
Доказательство
и ,
где – конечное число или бесконечно удаленная точка. Если эти пределы связаны неравенством ,
то существует такая проколотая окрестность точки , в которой
.
Доказательство ⇓
Доказательство свойств
Влияние значений функции в конечном числе точек на величину предела
Все свойства Если значения функции f(x) изменить (или сделать неопределенными) в конечном числе точек x1, x2, x3, ... xn,то это изменение никак не повлияет на существование и величину предела функции в произвольной точке x0.
Это следует из того, что в определение предела функции входят только значения независимой переменной из произвольной проколотой окрестности точки x0. Значение функции в самой точке x0 полностью исключается из рассмотрения. Функция может быть определена в этой точке, или не определена – на существование и величину предела в точке x0 это никакого влияния оказать не может.
Таким образом, если одна из точек, в которых производятся изменения значений функции, совпадает с x0, то это не может оказать влияния на величину или существование предела. Но, поскольку проколотая окрестность точки x0 выбирается произвольно, то мы всегда можем сузить ее границы, чтобы в нее не попали остальные точки, поскольку их число конечно. Поэтому, при вычислении предела, значения функции в конечном числе точек, не оказывают влияния на величину или существование предела в произвольной точке.
Теорема об ограниченности функции, имеющей конечный предел
Все свойства Если существует конечный предел ,то существует такая проколотая окрестность точки x0, в которой функция f(x) ограничена:
.
Пусть существует конечный предел
.
Воспользуемся определением предела функции по Коши.
Согласно этому определению, для любой окрестности точки a, существует такая проколотая окрестность точки , что для всех x, принадлежащих этой проколотой окрестности: , значения функции принадлежат окрестности точки a:
.
Поскольку число a конечно, то в качестве окрестности точки a возьмем ее ε - окрестность с : .
Тогда существует проколотая окрестность точки , так что для всех x, принадлежащих этой окрестности,
при .
Выполняем преобразования:
;
;
;
.
Итак, мы показали, что существует окрестность , для которой
при ,
где .
Теорема доказана.
Теорема об ограниченности снизу функции, имеющей ненулевой предел
Все свойства Пусть функция f(x) имеет в точке x0 конечный предел, отличный от нуля:.
Тогда, для любого числа c из интервала , существует такая проколотая окрестность точки x0, что для всех x, принадлежащих этой окрестности: ,
, если ;
, если .
Пусть существует конечный предел, отличный от нуля
.
Воспользуемся определением предела функции по Коши.
Согласно этому определению, для любой окрестности точки a, существует такая проколотая окрестность точки , что для всех x, принадлежащих этой проколотой окрестности: , значения функции принадлежат окрестности точки a:
.
В качестве окрестности точки a возьмем ее ε - окрестность:
.
Поскольку ε есть произвольное положительное число, то положим . Тогда существует проколотая окрестность точки , так что для всех x, принадлежащих этой окрестности,
при .
Раскрываем знак модуля и выполняем преобразования:
;
.
При , . Тогда
.
При , . Тогда
.
Теорема доказана.
Теорема о пределе постоянной функции
Все свойства Если в некоторой проколотой окрестности точки , – постоянная, то.
Пусть, на некоторой проколотой окрестности точки , функция является постоянной:
при .
Тогда в этой окрестности, для любого положительного ,
.
То есть для любого , существует такая проколотая окрестность точки , совпадающая с , для всех точек которой
при .
Согласно определению Коши это означает, что
.
Свойство доказано.
Теорема об односторонних пределах
Все свойства Функция имеет предел в точке тогда и только тогда, когдаона имеет в этой точке равные односторонние пределы.
Пусть существует конечный или бесконечный предел функции f в конечной или бесконечно удаленной точке :
.
Покажем, что существуют односторонние пределы, равные a.
Воспользуемся определением предела функции по Коши с использованием произвольных окрестностей. Согласно этому определению, для любой окрестности точки a, существует такая проколотая окрестность точки , на которой определена и
для всех .
Но двустороннюю проколотую окрестность можно представить как объединение левой и правой проколотых окрестностей. Тогда
для всех ;
для всех .
Это означает, что существуют односторонние равные пределы:
.
Примечание. Для бесконечно удаленной точки , под символами и мы понимаем и , соответственно.
Пусть теперь существуют равные односторонние пределы. Поскольку существует предел слева, то для любой окрестности точки a, существует такая проколотая левая окрестность точки , на которой определена и
для всех .
Поскольку существует предел справа, то для той же окрестности точки a, существует такая проколотая правая окрестность точки , на которой определена и
для всех .
Объединив окрестности и , получим проколотую двустороннюю, или просто проколотую окрестность точки :
.
Тогда, для выбранной нами произвольной окрестности ,
для всех .
Это означает, что
.
Свойство доказано.
Свойство пределов функций, связанных неравенством
Все свойства Если существуют конечные пределы и и в некоторой проколотой окрестности точки x0,
то .
Пусть есть произвольная последовательность, сходящаяся к : . И пусть ее элементы принадлежат проколотой окрестности точки , на которой выполняется неравенство
.
Рассмотрим последовательности и . Поскольку и , то согласно определению предела функции по Гейне, эти последовательности имеют пределы:
, .
Поскольку , то их элементы связаны неравенствами:
.
Тогда, согласно свойству неравенств,
.
Отсюда
.
Свойство доказано.
Теорема о функциях, пределы которых связаны неравенством
Все свойства Пусть существуют конечные пределы функций и :и ,
где – конечное число или бесконечно удаленная точка. Если эти пределы связаны неравенством ,
то существует такая проколотая окрестность точки , в которой
.
Для доказательства будем использовать универсальное определение предела функции по Коши.
Поскольку существует конечный предел , то для любого положительного , существует такая проколотая окрестность точки , в которой значения функции принадлежат ε - окрестности точки :
.
Поскольку существует конечный предел , то для любого положительного , существует такая проколотая окрестность точки , в которой значения функции принадлежат ε - окрестности точки :
.
Возьмем .
И пусть – пересечение окрестностей и :
, где .
Тогда для всех выполняются неравенства:
;
.
Раскроем знаки модуля:
;
.
К первому неравенству прибавим и оставим только правую часть. Ко второму неравенству прибавим и оставим только левую часть. В результате получаем:
;
.
Отсюда следует:
.
Или
при ,
где , .
Теорема доказана.
Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: Изменено:
