Определение производной функции в точке
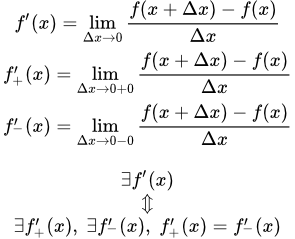
Определение производной
- Производная функции в точке
- Пусть функция f(x) определена в некоторой окрестности точки x0.
Производной f′(x0) функции f(x) в точке x0 называется конечный предел отношения приращения функции к приращению ее аргумента, когда последний стремится к нулю:
(1) f ′(x0) = limΔx → 0 Δ f Δx = limΔx → 0 f (x0 + Δx) – f (x0)Δx = limx1 → x0 f (x1) – f (x0)x1 – x0.
- Приращение аргумента функции
- f (x) в точке x0 – это разность значений аргумента в некоторой точке x1 и точке x0:
Δx = x1 – x0.
Приращение аргумента является независимой переменной. - Приращение функции
- f (x) в точке x0 – это разность значений функции в некоторой точке x1 = x0 + Δx и точке x0: Δ f = f (x0 + Δx) – f (x0) = f (x1) – f (x0).
Приращение функции является зависимой переменной. Оно зависит от x0 и Δx, или от x0 и x1. - Дифференцирование
- – это процесс вычисления производной.
В определении (1), приращение аргумента Δx является одной переменной, хотя ее обозначение состоит из двух букв: Δ и x. Обычно переменную принято обозначать одной буквой или буквой с одним или несколькими индексами. Но приращение в математическом анализе настолько часто встречается, что его обозначают с небольшим нарушением правил. Приращение функции Δ f также является одной переменной.
В приведенных выше определениях, Δx является независимой переменной, а Δ f – зависимой. Δ f зависит от двух переменных. Если использовать выражение Δ f = f (x0 + Δx) – f (x0), то приращение функции Δ f зависит от переменных x0 и Δx. Если использовать Δ f = f (x1) – f (x0), то Δ f зависит от x0 и x1. Но когда мы вычисляем производную в заданной точке x0, то считаем, что x0 является постоянной. Тогда Δ f Δx = f (x0 + Δx) – f (x0)Δx является функцией, зависящей только от одной переменной Δx. Таким образом задача о нахождении производной в точке x0 сводится к задаче о вычислении предела от функции ψ(Δx) = f (x0 + Δx) – f (x0)Δx, зависящей от одной переменной Δx при Δx → 0, или от функции φ(x1) = f (x1) – f (x0)x1 – x0, зависящей от одной переменной x1 при x1 → x0.
В правой части (1) мы сделали замену, и перешли от переменной Δx к переменной x1 = x0 + Δx. Тогда Δx = x1 – x0. При Δx → 0, x1 → x0,
limΔx → 0 f (x0 + Δx) – f (x0)Δx = limx1 → x0 f (x1) – f (x0)x1 – x0.
После того, как мы нашли производную в заданной точке, то x0 уже можно считать не фиксированным числом, а переменной. То есть предел (1) можно рассматривать как функцию от x0. Для удобства можно заменить обозначение переменной с x0 на x. Тогда (1) примет вид:
f ′(x) = limΔx → 0 f (x + Δx) – f (x)Δx = limx1 → x f (x1) – f (x)x1 – x.
Такая запись более удобна для восприятия в тех случаях, когда мы рассматриваем производную как функцию от той точки, в которой она вычисляется. Хотя от переобозначения переменной ничего не меняется.
Еще раз подчеркнем, что выражение f (x + Δx) – f (x)Δx является функцией от двух переменных: x и Δx. А выражение limΔx → 0 f (x + Δx) – f (x)Δx, полученное после вычисления предела, зависит только от одной переменной x.
Ниже приводятся примеры вычислений производных ⇓, используя определение ⇑.
Обозначение производной
Обозначение Лагранжа
Наиболее популярным является обозначение Лагранжа. Производную функции f (x) обозначают как и саму функцию, добавляя штрих после ее характеристики: f ′(x). Если функция задана алгебраическим выражением, то это выражение заключают в скобки, и ставят знак штриха справа за закрывающей скобкой: ( f (x)) ′. При этом производная также является функцией от той же переменной x, что и f (x). Правда область определения производной может не совпадать с областью определения функции, а является ее подмножеством.
Напомним, что в обозначении функции фигурируют три символа: независимая переменная, характеристика функции и зависимая переменная (см. «Определение функции»). Так, в выражении
(2) y = f (x),
x является независимой переменной, или аргументом функции; f – характеристикой функции; y – зависимой переменной, или значением функции. Обозначение зависимой переменной может совпадать или не совпадать с обозначением характеристики. Производную функции (2) обозначают так:
y ′ = f ′(x).
Независимую переменную производной обозначают так же, как и независимую переменную функции. В нашем случае это x.
Характеристику производной обозначают тем же символом, что и характеристику функции, добавляя штрих справа: f ′.
Зависимую переменную производной обозначают аналогично характеристике, добавляя штрих к обозначению зависимой переменной функции. Так, для примера (2), это будет y ′: y ′ = f ′(x).
Если функция зависит от нескольких переменных, например
(3) y = f (x1, x2, x3),
но все кроме одной считают постоянными, то к характеристике производной добавляют нижний индекс, обозначающий ту переменную, по которой вычисляют производную. При этом знак штриха может быть опущен. Например, следующие два обозначения эквивалентны: f ′x1(x1, x2, x3) ≡ f x1 (x1, x2, x3). Здесь подразумевается, что переменные x2 и x3 мы считаем постоянными. Тогда в данном контексте, f (x1, x2, x3) является функцией от одной переменной x1. К зависимой переменной производной также добавляют нижний индекс переменной, по которой выполняется дифференцирование:
y ′x1 ≡ yx1 = f ′x1(x1, x2, x3).
Подобные производные функций от нескольких переменных называются частными производными. Детально они будут рассмотрены позже.
Нижний индекс добавляют и при вычислениях, связанных со сложными функциями. Пусть, например, функцию y = f (x) можно представить как сложную: f (x) = g(t(x)), составленную из двух функций: y = g(t) и t = t(x). При этом множества значений функций f (x) и g(t) совпадают. Поэтому их удобно обозначить одной переменной y. Тогда производную от y, выраженную через переменную x, обозначают как y ′x:
y ′x = f ′(x).
А производную от y, выраженную через переменную t, обозначают как y ′t:
y ′t = g ′(t).
Обозначение производной по времени в физике
В механике и физике, производную по времени обозначают не штрихом, а точкой над зависимой переменной. Обычно время обозначают буквой t. Тогда
.y ≡ y ′t.
Обозначение Лейбница
В способе Лейбница, зависимую переменную обозначают в форме отношения дифференциалов:
dydx ≡ y ′x.
Этот способ удобен, поскольку указывает, по какой переменной ведется дифференцирование. Такой способ применяется только для функций от одной переменной. Для функций от многих переменных используют обозначение частной производной: ∂y∂x1.
Иногда в форме дифференциалов обозначают характеристику производной, добавляя справа аргумент:
dydx (x) ≡ y ′(x).
Однако этот способ скорее неудачен, и может привести к путанице.
Обозначение Коши
Также, для обозначения производной, используют обозначение Коши:
D y = D f (x).
Но мы не будем им пользоваться.
Существование производной
Рассмотрим вопрос о существовании предела, который используется при вычислении производной, при заданном значении x0:
(4) limΔx → 0 f (x0 + Δx) – f (x0)Δx.
Здесь могут возникнуть три случая:
1) в точке x0 существует конечный предел (4);
2) существует бесконечный предел +∞, или –∞;
3) предела (4) не существует.
1) Если существует конечный предел (4), то говорят, что функция имеет производную в точке x0.
2) Если в некоторой точке x0 существует бесконечный предел (4), то говорят, что производной в этой точке не существует. Однако при этом говорят, что функция f имеет в точке x0 бесконечную производную, равную +∞, или –∞.
Получается, что если предел равен бесконечности, то он существует, а ели производная равна бесконечности (которая является пределом), то ее не существует. Такое различие терминологии связано с тем, что наиболее фундаментальным понятием является дифференцируемость функции, которое нельзя определить в случае бесконечной производной.
3) Если предела (4) не существует, то функция не имеет производной в точке x0.
Производные справа и слева
Определение
- Правая (левая) производная функции f в точке x0
- Пусть функция f(x) определена в правой окрестности U(x0 + 0) точки x0. Тогда правой производной функции f в точке x0 называется правый предел
f ′+(x0) = limΔx → 0 + 0 Δ f Δx = limΔx → 0 + 0 f (x0 + Δx) – f (x0)Δx = limx1 → x0 + 0 f (x1) – f (x0)x1 – x0.
Соответственно, если функция определена в левой окрестности x0, то левой производной функции f в точке x0 называется левый предел
f ′–(x0) = limΔx → 0 – 0 Δ f Δx = limΔx → 0 – 0 f (x0 + Δx) – f (x0)Δx = limx1 → x0 – 0 f (x1) – f (x0)x1 – x0.
Правую (левую) производную также называют производной справа (слева) в точке x0, или правосторонней (левосторонней) производной в точке x0.
Лемма об односторонних производных
Функция f (x) имеет в точке x0 производную f ′(x0) тогда и только тогда, когдаона имеет в этой точке производные справа и слева, и они равны:
f ′+(x0) = f ′–(x0).
При этом
f ′(x0) = f ′+(x0) = f ′–(x0).
Для доказательства применим теорему об односторонних пределах.
Пусть существует производная функции f (x) в точке x0. Это означает, что она определена в некоторой окрестности U(x0) точки x0, и существует конечный предел
ψ(Δx) = f (x0 + Δx) – f (x0)Δx при Δx → 0:
f ′(x0) = limΔx → 0 ψ(Δx).
Но тогда существуют правая и левая окрестности точки x0, на которых f (x) определена. По теореме об односторонних пределах, существуют равные правый и левый пределы:
limΔx → 0 + 0 ψ(Δx) = limΔx → 0 – 0 ψ(Δx) = limΔx → 0 ψ(Δx).
Отсюда следует, что в точке x0 существуют односторонние производные
f ′+(x0) = f ′–(x0) = f ′(x0).
Пусть теперь, в точке x0, существуют равные односторонние производные:
f ′+(x0) = f ′–(x0).
Это означает, что существуют правая {x1 : x0 ≤ x1 < x0 + δ+} и левая {x1 : x0 – δ– < x1 ≤ x0} окрестности точки x0, в которой определена f (x). И существуют односторонние равные пределы:
limΔx → 0 + 0 ψ(Δx) = limΔx → 0 – 0 ψ(Δx).
Отсюда следует, что существует двусторонняя окрестность {x1 : x0 – δ– < x1 < x0 + δ+} точки x0, на которой определена f (x). И по теореме об односторонних пределах, существует двусторонний предел:
limΔx → 0 ψ(Δx) = limΔx → 0 + 0 ψ(Δx) = limΔx → 0 – 0 ψ(Δx).
Это означает, что в точке x0 существует производная
f ′(x0) = f ′+(x0) = f ′–(x0).
Лемма доказана.
Следствие о неравных односторонних производных
Если функция f (x) имеет в точке x0 не равные односторонние производные:f ′+(x0) ≠ f ′–(x0),
то она не имеет производной в этой точке.
Действительно, допустим противное. Пусть функция f (x) имеет в точке x0 не равные односторонние производные, но при этом имеет производную в этой точке. Тогда, согласно лемме об односторонних производных, она имеет в этой точке равные производные слева и справа, что противоречит предположению.
См. пример ⇓.
Примеры вычисления производной, используя определение
Все примеры Здесь и далее мы приводим подробные решения примеров, в которых нужно вычислить производную функции f (x), используя определение производной ⇑.
f (x) = x 2 решение ⇓ ; f (x) = 3 √ x ⇓ ; f (x) = | x | ⇓ .
Пример
Все примеры ⇑ Найти производную функции f (x) = x 2, используя определение производной.
Решение
Функция определена для всех x. Поэтому она определена в любой окрестности любой точки x0. Используем определение (1). Считаем, что x0 – фиксированное число, то есть что его значение задано. Найдем приращение функции в точке x0:
Δ f = f (x0 + Δx) – f (x0) = (x0 + Δx) 2 – x 20 =
x 20 + 2x0 Δx + (Δx) 2 – x 20 = 2x0 Δx + (Δx) 2.
Находим отношение приращения функции к приращению ее аргумента:
Δ f Δx = 2x0 Δx + (Δx) 2Δx = 2x0 + Δx.
Находим предел функции ψ(Δx) = Δ f Δx = 2x0 + Δx, зависящей от переменной Δx. При этом считаем, что x0 является фиксированным, заданным числом:
f ′(x0) = limΔx → 0 Δ f Δx = limΔx → 0(2x0 + Δx) = limΔx → 0(2x0) + limΔx → 0(Δx) = 2x0 + 0.
Итак, мы нашли производную:
f ′(x0) = 2x0.
Теперь x0 можно считать переменной, обозначим ее буквой x:
f ′(x) = (x 2) ′ = 2x.
Поскольку вычисленный нами предел существует, и является конечным числом для всех x, то функция f (x) = x 2 имеет производную для всех значений аргумента x.
Ответ
f ′(x) = (x 2) ′ = 2x.
Пример бесконечной производной +∞
Все примеры ⇑ Найдем производную функции y = 3 √ x .
Решение
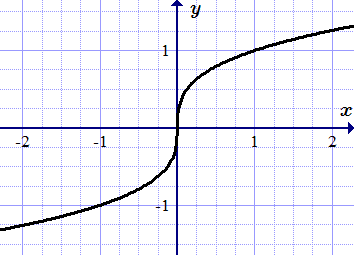
Функция f (x) = 3 √ x определена для всех x. Найдем отношение приращения функции к приращению ее аргумента в точке x0:
Δ f Δx = f (x1) – f (x0)x1 – x0 = 3 √ x1 – 3 √ x0 x1 – x0.
Применим формулу a 3 – b 3 = (a – b)(a 2 + ab + b 2). Тогда
x1 – x0 = ( 3 √ x1 ) 3 – ( 3 √ x0 ) 3 = ( 3 √ x1 – 3 √ x0 ) ⋅ ( 3 √ x 21 + 3 √ x1 x0 + 3 √ x 20 );
(5) Δ f Δx = 1 / ( 3 √ x 21 + 3 √ x1 x0 + 3 √ x 20 ).
Считаем, что x0 является фиксированным числом. Тогда отношение Δ f Δx является функцией от одной переменной x1: Δ f Δx = φ(x1). При x0 ≠ 0 она определена для всех x1. При x0 = 0 она определена для всех x1 ≠ 0.
Пусть x0 ≠ 0. Тогда:
f ′(x0) = limx1 → x0 13 √ x 21 + 3 √ x1 x0 + 3 √ x 20 = 13 √ x 20 + 3 √ x0 ⋅ x0 + 3 √ x 20 = 13 x –2 / 30.
Пусть x0 = 0. Подставим в (5) x0 = 0:
Δ f Δx = 1 / ( 3 √ x 21 + 3 √ x1 ⋅ 0 + 3 √ 0 2 ) = 1x 2 / 31.
Поскольку x 2 / 31 ≥ 0, то
f ′(0) = limx1 → 0 1x 2 / 31 = +∞.
Ответ
Таким образом мы нашли, что функция f (x) = 3 √ x имеет производную f ′(x) = 13 x –2 / 3 для всех x ≠ 0. При x = 0 функция не имеет производной, она равна +∞.
Пример
Все примеры ⇑ Найдем производную функции f (x) = | x | . Покажем, что несмотря на то, что функция определена для всех x, ее производная в точке x = 0 не существует.
Решение
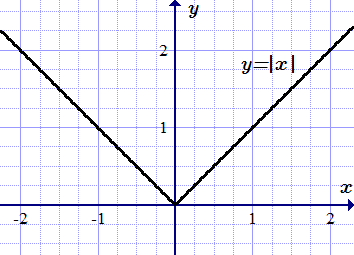
Функция f (x) = | x | определена для всех значений аргумента x. Поэтому она определена в любой окрестности произвольной точки x0.
1. Пусть x0 > 0. Тогда f (x0) = x0,
f ′(x0) = limΔx → 0 f (x0 + Δx) – f (x0)Δx = limΔx → 0 x0 + Δx – x0Δx = limΔx → 0 ΔxΔx = limΔx → 0 1 = 1.
2. Пусть x0 < 0. Тогда f (x0) = –x0,
f ′(x0) = limΔx → 0 f (x0 + Δx) – f (x0)Δx = limΔx → 0 –x0 – Δx – (–x0)Δx =
limΔx → 0 –ΔxΔx = limΔx → 0(–1) = –1.
3. Рассмотрим точку x = 0. В ней
ψ(Δx) = f (x + Δx) – f (x)Δx|x = 0 = f (0 + Δx) – f (0)Δx = | 0 + Δx | – | 0 | Δx = | Δx | Δx.
Найдем производную справа в точке x = 0. При этом Δx > 0, | Δx | = Δx,
f ′+(0) = limΔx → 0 + 0 ψ(Δx) = limΔx → 0 + 0 | Δx | Δx = limΔx → 0 + 0 ΔxΔx = limΔx → 0 + 0 1 = 1.
Теперь найдем производную слева в точке x = 0. В этом случае Δx < 0, | Δx | = –Δx,
f ′–(0) = limΔx → 0 – 0 ψ(Δx) = limΔx → 0 – 0 | Δx | Δx = limΔx → 0 – 0 –ΔxΔx = limΔx → 0 + 0(–1) = –1.
Итак, мы нашли, что односторонние производные в точке x = 0 существуют, но они не равны друг другу:
f ′+(0) = 1; f ′–(0) = –1.
Согласно следствию леммы об односторонних производных, производной функции f (x) = | x | в точке x = 0 не существует.
Ответ
f ′(x) = 1, x > 0;
f ′(x) = –1, x < 0;
f ′+(0) = 1; f ′–(0) = –1.
В точке x = 0 производная не существует.
Использованная литература:
Г.Е. Иванов. Лекции по математическому анализу. Часть 1. Москва, МФТИ, 2018.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: Изменено: