Метод интегрирования неопределенного интеграла по частям

Представлен метод интегрирования неопределенного интеграла по частям. Даны примеры интегралов, вычисляющихся этим методом. Разобраны примеры решений.

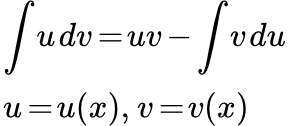
Формула интегрирования по частям

Формула интегрирования по частям имеет вид:
.

Метод интегрирования по частям состоит в применении этой формулы. Здесь стоит отметить, что u и v являются функциями от переменной интегрирования. Пусть переменная интегрирования обозначена как x (символ после знака дифференциала d в конце записи интеграла) . Тогда u и v являются функциями от x: u = u(x), v = v(x).
Тогда
,     .
И формула интегрирования по частям принимает вид:
.

То есть подынтегральная функция должна состоять из произведения двух функций:
,
одну из которых обозначаем как u:   g(x) = u, а у другой должен вычисляться интеграл (точнее находиться первообразная):
, тогда dv = f(x) dx.

В некоторых случаях f(x) = 1. То есть в интеграле
,
можно положить g(x) = u, x = v.

Резюме

Итак, в данном методе, формулу интегрирования по частям стоит запомнить и применять в двух формах:
;
.

Интегралы, вычисляющиеся интегрированием по частям

Интегралы, содержащие логарифм и обратные тригонометрические (гиперболические) функции

По частям часто интегрируются интегралы, содержащие логарифм и обратные тригонометрические или гиперболические функции. При этом ту часть, которая содержит логарифм или обратные тригонометрические (гиперболические) функции обозначают через u, оставшуюся часть – через dv.

Интегралы, содержащие произведение многочлена и sin x, cos x или e^x

По формуле интегрирования частям находятся интегралы вида:
,   ,   ,
где P(x) – многочлен от x. При интегрировании, многочлен P(x) обозначают через u, а e^ax dx, cos ax dx или sin ax dx – через dv.

Примеры вычисления интегралов методом интегрирования по частям

В этом разделе рассмотрены следующие примеры решений неопределенных интегралов:
               

Пример вычисления интеграла, содержащего логарифм

Пример

Вычислить интеграл:

Подробное решение

Здесь подынтегральное выражение содержит логарифм. Делаем подстановки
u = ln x,
dv = x² dx.
Тогда
,
.

.

Вычисляем оставшийся интеграл:
.
Тогда
.
В конце вычислений нужно обязательно добавить постоянную C, поскольку неопределенный интеграл – это множество всех первообразных. Также ее можно было добавлять и в промежуточных вычислениях, но это лишь загромождало бы выкладки.

Более короткое решение

Можно представить решение и в более коротком варианте. Для этого не нужно делать подстановки с u и v, а можно сгруппировать сомножители и применить формулу интегрирования по частям во втором виде.

Ответ

Пример вычисления интеграла, содержащего произведение многочлена и e^x

Пример

Вычислить интеграл:
.

Решение

Введем экспоненту под знак дифференциала:
e ^{– x} dx = – e ^{– x} d(–x) = – d(e ^{– x}).

Интегрируем по частям.
.
Также применяем метод интегрирования по частям.
.
.
.
Окончательно имеем:
.

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 19-10-2014