Дифференциальные уравнения высших порядков, не содержащие функцию в явном виде

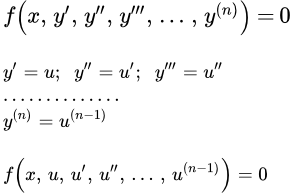
Рассмотрен метод решения дифференциального уравнения высшего порядка, не содержащего функцию y в явном виде. В таком уравнении порядок понижается с помощью подстановки. Даны подробные примеры решений подобных уравнений.

Метод решения

Рассмотрим уравнение, не содержащие функцию в явном виде:
(1)    f (x, y^′, y^′′, y^′′′,..., y^(n ) )  = 0 . 
Порядок этого уравнения понижается на единицу с помощью подстановки
y^′ = u . 

Действительно, тогда:
y^′′ = (y^′ ) ^′ = u^′ ; 
y^′′′ = (y^′ ) ^′′ = u^′′ ; 
...
y^(n )  = (y^′ ) ^{(n – 1 )}  = u^{(n – 1 )}  . 
И мы получили уравнение, в котором порядок понижен на единицу:
 f (x, u, u^′, u^′′,..., u^{(n – 1 )} )  = 0 . 

Пример 1

Решить уравнение:
y^′′′ + y^′′ 2  = 0

Решение

Делаем подстановку:
y^′′ = u . 
Тогда:
y^′′′ = (y^′′ ) ^′ = u^′ . 
Подставляем:
u^′ + u²  = 0 . 

Разделяем переменные:
dudx = – u²  . 
При u ≠ 0 имеем:
duu²  = – dx . 

Интегрируем:
∫ duu²  = – ∫ dx = – x – C₁  . 
Или:
– 1u = – x – C₁  . 
Отсюда:
y^′′ = u = 1x + C₁   . 

Интегрируем:
y^′ = ∫ dxx + C₁  = ln  | x + C₁  |  + C₂  . 
Интегрируем еще раз:
y = ∫ ln  | x + C₁  |  dx + C₂  ⋅ x . 

Интегрируем по частям:
∫ ln  | x + C₁  |  dx =  ∫ ln  | x + C₁  |  d (x + C₁ )  = 
= (ln  | x + C₁  | )  ⋅ (x + C₁ )  –  ∫ (x + C₁ )  ⋅ (ln  | x + C₁  | ) ^′dx = 
= (ln  | x + C₁  | )  ⋅ (x + C₁ )  –  ∫ (x + C₁ )  ⋅ 1x + C₁  dx = 
= (ln  | x + C₁  | )  ⋅ (x + C₁ )  –  ∫ dx = (x + C₁ )  ⋅ ln  | x + C₁  |  – x + C₃  . 

Окончательно имеем:
y = (x + C₁ )  ⋅ ln  | x + C₁  |  –  x + C₂ x + C₃  . 
Заменим постоянную:
C₂  – 1 → C₂  . 
Тогда
y = (x + C₁ )  ⋅ ln  | x + C₁  |  +  C₂ x + C₃  . 

Теперь рассмотрим случай:
y^′′ = u = 0 . 
u = 0 также является решением исходного уравнения. Интегрируем:
y^′ = C₁  ; 
y = C₁ x + C₂  . 

Ответ

y = (x + C₁ )  ⋅ ln  | x + C₁  |  +  C₂ x + C₃  ; 
y = C₁ x + C₂  . 

Пример 2

Решить уравнение:
(2.1)   (1 + x² ) y^′′ + y^′ 2  + 1 = 0 . 

Решение

Уравнение не содержит явно функцию y . Делаем подстановку
y^′ = u ,  где u – функция от x . Тогда
y^′′ = u^′ . 

Подставляем в исходное уравнение.
(2.2)   (1 + x² ) u^′ + u²  + 1 = 0 . 
Разделяем переменные и интегрируем.
(1 + x² ) dudx + u²  + 1 = 0 ; 
duu²  + 1 + dx1 + x²  = 0 ; 
∫ duu²  + 1 + ∫ dx1 + x²  = C₁  ; 
(2.3)   arctg u + arctg x = C₁  . 

Применим формулу суммы арктангенсов.
arctg u + arctg x = arctg u + x1 – ux  при ux < 1 ; 
arctg u + arctg x =  ± π + arctg u + x1 – ux  при ux > 1 . 
Подставим в (2.3), включив постоянную ± π ,  если возникнет, в C₁  . 
При ux ≠ 1 имеем.
arctg u + x1 – ux = C₁  .  Отсюда
u + x1 – ux = tg C₁  . 
Заменим постоянную tg C₁  → C₁  . 
(2.4)   u + x1 – ux = C₁  . 

Из последней формулы выражаем u , подставляем u = y^′ ,  и интегрируем.
u + x = C₁ (1 – ux )  ; 
u + C₁ ux = C₁  – x ; 
u (1 + C₁ x )  = C₁  – x ; 
y^′ = u = C₁  – x1 + C₁ x =  C₁  – (1 + C₁ x )  / C₁  + 1 / C₁ 1 + C₁ x =  C₁  + 1 / C₁ 1 + C₁ x – 1C₁   . 
При C₁  ≠ 0 имеем.
y = C²₁  + 1C₁  ∫ dx1 + C₁ x –  1C₁  ∫ dx + C₂  =  C²₁  + 1C²₁  ∫ d (1 + C₁ x ) 1 + C₁ x –  xC₁  + C₂  = 
 C²₁  + 1C²₁  ln  | 1 + C₁ x |  – xC₁  + C₂  ; 
(2.5)   y = C²₁  + 1C²₁  ln  | 1 + C₁ x |  – xC₁  + C₂  . 

Мы получили общее решение, пологая ux ≠ 1 и C₁  ≠ 0 .  Теперь исследуем эти случаи, исключенные из рассмотрения.

Пусть ux = 1 .  Отсюда
y^′ = u = 1x  . 
Интегрируем.
y = ∫ dxx + C₂  = ln  | x |  + C₂  . 
Нетрудно проверить, что функция
(2.6)   y = ln  | x |  + C₂  является решением исходного уравнения.

Рассмотрим значение постоянной C₁  = 0 .  Из (2.4), имеем.
u + x = 0 ; 
y^′ = u = – x . 
Интегрируем.
y = – ∫ x dx + C₂  = – x² 2 + C₂  . 
Функция y = – x² 2 + C₂  также является решением исходного уравнения.

В заключении можно упростить вид общего решения (2.5), если вместо постоянной C₁  использовать отличную от нуля постоянную ^~C₁  с помощью подстановки C₁  = 1 / ^~C₁  .  В общем решении C₁  ≠ 0 .  Поэтому такая замена не приведет к потере решения. Подставляем C₁  = 1 / ^~C₁  в (2.5).
y = ( 1 + 1C²₁   ) ln  | 1 + x / ^~C₁  |  –  ^~C₁ x + C₂  =  (1 + ^~C²₁ ) ln | ^~C₁  + x^~C₁   |  – ^~C₁ x + C₂  = 
 (1 + ^~C²₁ ) ln  | ^~C₁  + x |  –  (1 + ^~C²₁ ) ln  | ^~C₁  |  – ^~C₁ x + C₂  . 
Постоянную – (1 + ^~C²₁ ) ln  | ^~C₁  |  включим в C₂   : 
(2.7)   y = (1 + ^~C²₁ ) ln  | ^~C₁  + x |  – ^~C₁ x + C₂  . 
Выше мы наложили условие ^~C₁  ≠ 0 .  Однако, при ^~C₁  = 0 получается частное решение (2.6). Поэтому ^~C₁  может принимать любые значения, а решение (2.6) содержится в (2.7). Наконец, переобозначив ^~C₁  → C₁  ,  получаем окончательно.

Ответ

y = (1 + C²₁ ) ln  | x + C₁  |  – C₁ x + C₂  ; 
y = – x² 2 + C₂  . 

Автор: Олег Одинцов.     Опубликовано: 17-07-2013   Изменено: 18-02-2025