Однородные относительно функции и ее производных дифференциальные уравнения высших порядков

Показано как распознать дифференциальное уравнение, однородное относительно функции и ее производных. Рассмотрен способ решения таких уравнений. Дан пример подробного решения однородного дифференциального уравнения второго порядка.

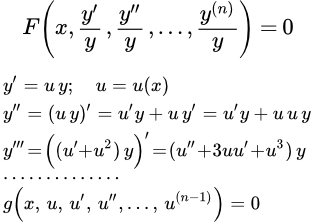
Дифференциальное уравнение высшего порядка, однородное относительно функции и ее производных

– это уравнение вида
, где функция обладает свойством
,   .
Такие уравнения можно выразить через произвольную функцию:
.

Как распознать однородное дифференциальное уравнение высшего порядка

Для того, чтобы распознать дифференциальное уравнение, однородное относительно функции и ее производных, нужно ввести постоянную t и сделать замену y → ty, y' → ty', y'' → ty'', и т.д. Если, в результате такого преобразования, постоянная t сократится, то это дифференциальное уравнение, однородное относительно функции и ее производных.

Решение однородного дифференциального уравнения

Однородное дифференциальное уравнение высшего порядка допускает понижение порядка с помощью подстановки:
,
где u – функция от x.
Действительно, тогда:
;

.
И т. д. Отсюда
;
;
.
И т. д. При подстановке в исходное уравнение
,
получаем уравнение относительно u, порядок которого понижен на единицу:
.

Пример решения однородного дифференциального уравнения высшего порядка

Решить уравнение:
.

Решение

Проверим, является ли данное уравнение однородным относительно функции и ее производных. Делаем замену
y → ty, y′ → ty′, y′′ → ty′′:
;
Или
.
t сокращается. Поэтому это однородное уравнение.

Делаем подстановку:
.
Тогда:
.
Подставляем в исходное уравнение:
.
Сокращаем на y² :
;
;
;
.

Это линейное дифференциальное уравнение первого порядка. Оно решается с помощью интегрирующего множителя, который в данном случае равен единице:
.
Отсюда:
;
;
.
Умножаем на dx и интегрируем:
;
.

Интегралы табличные:
.
Потенцируем (знак модуля сводится к умножению на постоянную ±1, которую включаем в C₂):
.
Заменим постоянную C₁ → - C₁.

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 19-07-2013