Дифференциальные уравнения высших порядков, решаемые в квадратурах
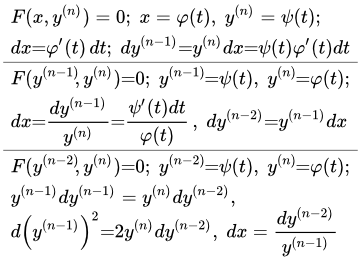
Здесь рассмотрены методы решения дифференциальных уравнений высших порядков, решаемые в квадратурах, то есть решения которых можно выразить через конечное число интегралов. К таким уравнениям относятся следующие типы:
⇓
⇓
⇓
Также приводятся подробно разобранные примеры решений ⇓ таких уравнений.
F(x, y(n)) = 0: Дифференциальные уравнения, содержащее только независимую переменную и производную n-го порядка
Рассмотрим дифференциальное уравнение высшего порядка, содержащее только независимую переменную x и производную n-го порядка :
(1) .
y(n) = f(x) Разрешенные относительно старшей производной
Если уравнение (1) удастся разрешить относительно производной, то есть представить в виде
(1.1) ,
то оно решается непосредственным интегрированием.
x = f(y(n)) Разрешенные относительно независимой переменной
Рассмотрим случай, когда уравнение (1) можно разрешить относительно переменной x. В этом случае, независимая переменная является функцией от старшей производной:
(1.2.1) .
Это уравнение можно решить в квадратурах в параметрическом виде, последовательно понижая порядок.
Вводим параметр t:
(1.2.2) .
Тогда из (1.2.1) получаем:
(1.2.3) .
При переходе к параметрическому виду (1.2.2) – (1.2.3), независимой переменной становится параметр t, а переменные и x – зависимыми от параметра t.
Возьмем дифференциал от (1.2.3):
;
(1.2.4) .
Выразим производную n-го порядка через производную порядка n–1, воспользовавшись уравнением:
.
Учитывая (1.2.2), и подставляя (1.2.4), находим выражение дифференциала производной n–1 - го порядка через параметр t:
.
Интегрируя, получаем выражение производной n-1 - го порядка через параметр t:
(1.2.5) .
Это уравнение, вместе с (1.2.3), дает выражение производной меньшего порядка в параметрическом виде:
Далее выражаем дифференциал производной порядка n – 2:
.
Подставляя (1.2.4) и (1.2.5), получаем дифференциал, выраженный через параметр t. После чего интегрируем по t, и, вместе с уравнением , получаем выражение производной в параметрическом виде. И так далее, пока получим зависимость функции y от параметра t.
F(x, y(n)) = 0 Общий случай
Теперь рассмотрим дифференциальное уравнение высшего порядка, содержащее только старшую производную и независимую переменную в общем случае:
(1.3.1) .
Это уравнение можно разрешить в квадратурах, если удастся представить уравнение (1.3.1) в параметрическом виде. То есть если удастся подобрать такие функции , для которых
(1.3.2) ,
и при этом уравнение (1.3.1) окажется эквивалентным уравнениям
(1.3.3) .
Тогда уравнение можно решить в квадратурах. Для этого сначала выразим дифференциал независимой переменной x через параметр t, используя первое уравнение (1.3.3):
.
После этого выражаем через параметр t дифференциал производной n-1-го порядка:
.
Интегрируя это уравнение по переменной t, получаем выражение для производной n-1-го порядка в параметрическом виде:
.
Где .
Далее выражаем через t дифференциал производной n-2-го порядка:
.
Интегрируя, получим параметрическое представление производной n-2-го порядка. И так далее, пока получим параметрическое представление функции y.
F(y(n-1), y(n)) = 0 Уравнения, содержащие только производные порядков n и n-1
Общий случай
Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-1-го порядков:
(2.1.1) .
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
(2.1.2) .
Тогда если положить
(2.1.3) ,
то уравнение (2.1.1) будет выполняться автоматически. При этом должно соблюдаться еще одно условие – чтобы представления (2.1.1) и (2.1.3) были эквивалентными. То есть, чтобы при переходе от одного представления к другому, не появились новые и не терялись существующие решения.
Если найдено такое параметрическое представление уравнения (2.1.1), то его можно решить в квадратурах. Для этого, как и в предыдущем случае, сначала выразим дифференциал независимой переменной x через параметр t. Преобразуем первое уравнение (2.1.3):
.
Отсюда
;
(2.1.4) .
Интегрируя, получаем выражение независимой переменной x через параметр t:
(2.1.5) .
Тем же способом, что и в предыдущем случае, выражаем производные и меньших порядков через t:
.
Интегрируем:
.
Продолжая процесс, получаем выражения остальных производных и самой функции y через параметр t. Вместе с уравнением (2.1.5), это дает решение исходного уравнения в параметрическом виде.
y(n-1) = f(y(n)) Разрешенные относительно младшей производной
Рассмотрим частный случай уравнения (2.1.1), в котором производная меньшего порядка выражена через старшую производную:
.
Это уравнение интегрируется в квадратурах, введением параметра
.
Тогда
.
Из этих уравнений
;
;
;
.
;
.
Тем же способом находим выражение через t производных и переменной y.
y(n) = f(y(n-1)) Разрешенные относительно старшей производной
Рассмотрим второй частный случай, когда старшая производная выражена через производную меньшего порядка:
(2.3.1) .
Вводим параметр
(2.3.2) .
Тогда
.
Из этих уравнений
;
;
;
(2.3.3) .
Если уравнение (2.3.3) удастся разрешить относительно t, то получим зависимость вида . Учитывая (2.3.2), получаем уравнение, в котором производная n–1-го порядка является функцией от независимой переменной:
.
Интегрируя это уравнение n–1 раз, получим зависимость y от x. См. Дифференциальное уравнение y(n) = f(x)
Но в любом случае можно получить решение в параметрическом виде.
;
.
Тем же способом находим выражение через t производных и переменной y.
F(y(n-2), y(n)) = 0 Уравнения, содержащие только производные порядков n и n-2
Общий случай
Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-2-го порядков:
(3.1.1) .
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
(3.1.2) .
Положим
(3.1.3) .
Тогда уравнение (3.1.1) выполняется автоматически. Считаем также, что представления (3.1.1) и (3.1.3) эквивалентны.
Для решения уравнения запишем дифференциалы производных порядков n-1 и n-2:
.
Исключаем dx. Из второго уравнения
(3.1.4) .
Подставим в первое и преобразуем:
;
;
.
Подставляя (3.1.3) и интегрируя, получим выражение производной через параметр t:
;
;
;
.
Знак плюс или минус выбирается из начальных условий, как и постоянная интегрирования .
Из (3.1.4) находим выражение x через t:
(3.1.5) ;
(3.1.6) .
Далее, как и в предыдущих случаях находим выражения производных и зависимой переменной y через t. Например,
;
;
и так далее.
Примечание. В литературе иногда не ставят знак плюс-минус. При этом подразумевают, что корень является многозначной функцией и автоматически может быть как положительным, так и отрицательным.
y(n) = f(y(n-2)) Разрешенные относительно старшей производной
Сведем к квадратурам уравнение, разрешенное относительно старшей производной:
(3.2.1) .
Введем новую переменную:
(3.2.2) .
Тогда исходное уравнение (3.2.1) станет уравнением второго порядка:
(3.2.3) .
Это, так называемое, дифференциальное уравнение Ньютона. Умножим его на и выделим полную производную:
;
.
Отсюда получаем первый интеграл:
.
Находим выражение для дифференциала . Для этого извлекаем квадратный корень:
.
Отсюда
(3.2.4) .
Знак плюс или минус выбирается из начальных условий. В общем решении допустим любой знак.
Интегрируя, получаем зависимость u от x в неявном виде:
(3.2.5) .
Если после интегрирования удастся разрешить u относительно x, то, поскольку , мы получим уравнение вида (1.1), которое решается последовательным интегрированием.
Если уравнение (3.2.5) разрешить относительно u не удастся, то решаем в параметрическом виде, как это описывалось ранее. То есть вводим параметр . Тогда (3.2.5) и (3.2.4) дают выражения переменной x и ее дифференциала через t:
(3.2.6) .
(3.2.7) .
Далее, уравнение
вместе с (3.2.7) дают параметрическое представление зависимости производной порядка n - 2 от переменной x.
Используя (3.2.6), можно найти параметрическое представление остальных производных и самой функции y от переменной x. Например,
;
.
И так далее.
Примеры решений задач
Все примеры Далее рассматриваются примеры с подробными решениями следующих дифференциальных уравнений.
⇓
⇓
⇓
⇓
⇓
Пример 1
Найти общее решение дифференциального уравнения третьего порядка, содержащего только старшую производную и независимую переменную.
(П1.1) .
Решение
По всей видимости, в уравнении (П1.1) выразить через x в элементарных функциях или не возможно, или довольно сложно. Мы не будем пытаться это делать, поскольку здесь независимая переменная x выражена через производную . Поэтому решаем задачу в параметрическом виде.
Вводим параметр t. Получаем параметрические уравнения, эквивалентные (П1.1):
(П1.2) .
Выразим дифференциал переменной x через параметр t:
;
(П1.3) .
Используя (П1.2) и (П1.3), выражаем дифференциал производной второго порядка через параметр t:
.
Интегрируем.
;
(П1.4) .
Используя (П1.3) и (П1.4), аналогично предыдущему имеем:
;
.
Наконец, находим y.
;
;
.
Ответ
;
.
Пример 2
Найти частное решение дифференциального уравнения второго порядка, содержащее только вторую производную и независимую переменную:
(П2.1) ;
(П2.2) .
Решение
Это уравнение является кубическим по отношению ко второй производной , и уравнением седьмой степени (если умножить его на x) по отношению к независимой переменной x. Можно попытаться разрешить его относительно или x, но здесь есть более простой способ.
Заметим, что уравнение (П2.1) выполняется, если выразить зависимость от x, определяемую уравнением (П2.1) в параметрическом виде:
(П2.3) .
Действительно, подставляя (П2.3) в (П2.1) получаем:
;
;
.
То есть если взять параметрическое представление (П2.3), то уравнение (П2.1) выполняется.
Однако это не означает, что представление (П2.3) автоматически эквивалентно уравнению (П2.1). Поскольку кубическое уравнение может иметь три действительных корня, то, возможно, уравнение (П2.3) можно представить в параметрическом виде тремя неэквивалентными способами. Также возможен случай, когда условия теоремы существования и единственности решения дифференциального уравнения не выполняются, и заданным начальным условиям будут удовлетворять несколько решений. Все это нужно иметь в виду при решении подобных уравнений. Но нам нужно найти любое решение, удовлетворяющее заданным начальным условиям. Поэтому попробуем применить для этой цели представление (П2.3).
Выразим дифференциал независимой переменной x через дифференциал параметра t, используя (П2.3):
.
Выразим дифференциал производной через параметр t и его дифференциал:
.
Интегрируем:
. Найдем значение постоянной , используя первое начальное условие (П2.2). Из (П2.3) находим: . При . При . Отсюда .
Итак, мы нашли параметрическое представление для производной:
.
Аналогично предыдущему, выражаем y через параметр t:
;
.
Находим значение постоянной , используя второе начальное условие (П2.2). При . При . Отсюда .
Тем самым мы нашли частное решение в параметрическом виде:
.
Выразим t через x.
;
.
Ответ
.
Пример 3
Решить дифференциальное уравнение, содержащее только производные первого и второго порядков:
(П3.1) .
Решение
Нетрудно видеть, что если положить
(П3.2) ,
то уравнение (П3.1) выполняется автоматически. Поэтому решаем это уравнение в параметрическом виде.
Выразим дифференциал независимой переменной x через параметр t.
;
;
(П3.3) .
Интегрируя (П3.3), получаем выражение независимой переменной x через параметр t:
;
(П3.4) .
Используя формулу , и применяя выражение через t (см. (П3.2)), выразим дифференциал dy через t:
.
Интегрируя, находим выражение зависимой переменной через параметр t:
.
Итак, мы нашли зависимость в параметрической форме:
.
Отсюда можно получить зависимость y от x в явном виде. Из второго уравнения, . Подставляем в первое:
.
Ответ
.
Пример 4
Решить дифференциальное уравнение, содержащее только производные второго и третьего порядков:
(П4.1) .
Решение
Это дифференциальное уравнение содержит только производные второго и третьего порядков. При этом оно разрешено относительно высшей производной. Решаем параметрическим методом. За параметр t возьмем производную второго порядка:
(П4.2) .
Выразим дифференциал независимой переменной x через параметр t. Из (П4.1) имеем:
;
;
(П4.3) .
Выразим независимую переменную x через параметр t. Для этого интегрируем (П4.3):
;
(П4.4) .
См. Обратные гиперболические функции, их графики и формулы
Выразим дифференциал через параметр t и, интегрируя, выразим производную через t:
;
;
(П4.5) .
Выразим дифференциал зависимой переменной y через параметр t. После чего интегрируя, выразим y через t:
;
;
(П4.6) .
Исключим параметр t из уравнений (П4.4) т (П4.6).
;
.
Примечание.
Эту задачу можно решить проще, если с самого начала выбрать следующее параметрическое представление для производных:
.
Ответ
.
Пример 5
Решить дифференциальное уравнение с заданными начальными условиями:
(П5.1) ;
(П5.2) .
Решение
Уравнение имеет вид (3.2.3). В нем вторая производная выражена через функцию (зависимую переменную y). Решаем изложенным выше методом ⇑.
Умножим исходное уравнение (П5.1) на и выделяем полный дифференциал.
;
;
;
.
Извлекаем квадратный корень:
(П5.3) .
Найдем значение постоянной и знак корня из начальных условий (П5.2). Для этого подставляем в (П5.3) :
.
Отсюда видно, что нужно взять знак плюс и . Тогда
.
Разделяем переменные и интегрируем.
;
;
;
(П5.4) .
Определяем значение постоянной . Для этого подставляем значения начальных условий (П5.2): :
.
Отсюда . Подставляем в (П5.4):
.
Возводим в квадрат и выполняем преобразования:
;
.
Извлекаем квадратный корень:
.
Выбираем знак плюс или минус из начальных условий (П5.2). Подставляем :
.
Этому уравнению удовлетворяет знак плюс. Тогда
.
Ответ
.
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Автор: Олег Одинцов. Опубликовано:
