Дифференциальные уравнения высших порядков, не содержащие переменную в явном виде

Рассмотрен метод решения дифференциального уравнения высшего порядка, не содержащего переменную x в явном виде. Такое уравнение сводится к уравнению более низкого порядка с помощью подстановки. Дан подробный пример решения такого уравнения.

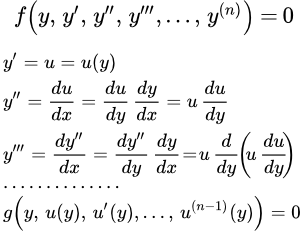
Метод решения

Рассмотрим уравнение, не содержащее независимую переменную в явном виде:
(1)   .
Порядок этого уравнения понижается на единицу с помощью подстановки:

Далее считаем, что функция u зависит от переменной y, тогда:
;
;
и т. д.

В результате такой подстановки, порядок уравнения понижается на единицу.

Пример

Решить уравнение:
.

Решение

Уравнение не содержит независимую переменную в явном виде. Делаем подстановку:
.
Считаем, что функция u зависит от переменной y. Тогда
.

Подставляем в исходное уравнение:
.
Делим на u. При имеем:
.
Это уравнение с разделяющимися переменными. Делим на   и умножаем на dy. При   имеем:
.
Интегрируем:
(2)   .

Вычисляем интегралы.
;
;
.

Подставляем в (2):
.
Потенцируем:
.
Заменим постоянную интегрирования . Знак модуля сводится к умножению на ±1. Включим ±1 в постоянную . То есть мы теперь полагаем, что может быть не только положительным, но и отрицательным числом. Тогда:
.

Выполняем преобразования:
;
.
При    имеем:
;
.

Разделяем переменные:
.
Интегрируем:
(3)   .

Вычисляем интеграл:

.
Подставляем в (3):
;
.
Возводим в квадрат и выполняем преобразования:
;
;
(4)   .

При выводе формулы (4) мы предполагали, что
  и   .
Теперь рассмотрим случаи
.
Нетрудно видеть, что решение, охватывающее эти три равенства, есть
(5)   ,
где C – произвольная постоянная. Тогда . Подставляя это в исходное уравнение нетрудно убедиться, что оно выполняется. Это особое решение. Добавим его в ответ.

Ответ

;
.

Автор: Олег Одинцов.     Опубликовано: 18-07-2013   Изменено: 27-06-2018