Методы решения физико-математических задач

Производная функции на интервале

Теорема Лагранжа
Приводятся формулировки свойств и теорем, применяемых для исследования поведения функции на интервале с помощью производных.
Содержание

Локальные экстремумы

Локальный минимум (максимум)
Пусть функция определена в некоторой окрестности точки .
Функция имеет в точке локальный минимум, если существует такая проколотая окрестность точки , на которой
при .
Если выполняется строгое неравенство , то говорят, что в точке
строгий локальный минимум. В противном случае – нестрогий локальный минимум.

Функция имеет в точке локальный максимум, если
при .
Если выполняется строгое неравенство , то говорят, что в точке
строгий локальный максимум. В противном случае – нестрогий локальный максимум.

Локальный экстремум
– это локальный минимум или локальный максимум.
Строгий локальный экстремум
– это строгий локальный минимум или строгий локальный максимум.
Нестрогий локальный экстремум
– это нестрогий локальный минимум или нестрогий локальный максимум.

Теоремы о среднем

Теорема о необходимом условии экстремума (Ферма)
Если точка является точкой локального экстремума (строгого или нестрогого) функции
и она дифференцируема в этой точке,
то .
Доказательство
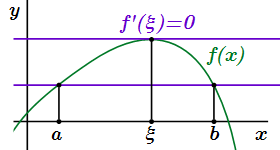
Теорема Ролля о нулях производной
Теорема Ролля о нулях производной
Теорема Ролля о нулях производной
Пусть функция
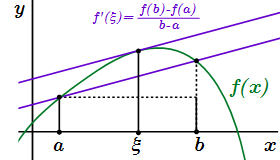
1) непрерывна при ;
2) дифференцируема при ;
3) .
Тогда существует точка такая, что производная функции в ней равна нулю:
, где .
Теорема Лагранжа конечных приращений
Теорема Лагранжа конечных приращений
Теорема Лагранжа конечных приращений
Пусть функция
1) непрерывна при ;
2) дифференцируема при .
Тогда существует точка такая, что производная функции в ней равна угловому коэффициенту прямой, проведенной через точки и :
, где .
Или
, где .
Формула конечных приращений Лагранжа
– это следующая формула:
, где ;
где функция непрерывна на отрезке и дифференцируема внутри него.
Ее также можно записать в следующем виде:
, где ;
где функция непрерывна на отрезке с концами и дифференцируема внутри него.
Формула бесконечно малых приращений
,
где функция дифференцируема в точке .
Теорема Коши обобщенных конечных приращений
Пусть функции
1) непрерывны при ;
2) дифференцируемы при ;
3) при .
Тогда существует точка , для которой справедлива формула конечных приращений Коши:
.
Если обозначить , то предыдущая формула примет вид:
.

Следствия из теоремы Лагранжа

Свойство функции с равной нулю производной
Если функция дифференцируема на интервале
и ее производная равна нулю:
при ,
то функция есть постоянная, не зависящая от величина:
  при .
Свойство двух функций с равными производными
Пусть функции и дифференцируемы на интервале .
И пусть при .
Тогда функции и различаются на постоянную величину:
  при .

Свойства производной

Теорема Дарбу о промежуточных значениях производной
Пусть функция
дифференцируема на интервале .
Тогда ее производная принимает на интервале все значения, заключенные между и :
.
Теорема о пределе производной
Пусть функция
1) дифференцируема в некоторой проколотой окрестности точки ;
2) непрерывна в точке ;
Если существует конечный или бесконечный предел производной
,
то существует производная в , равная этому пределу:
.
Если существует конечный или бесконечный левый предел производной
,
то существует левая производная в , равная этому пределу:
.
Если существует конечный или бесконечный правый предел производной
,
то существует правая производная в , равная этому пределу:
.

Эту теорему можно записать в символическом виде.
Если непрерывна в , то
.
Здесь или .
Выразив производную через приращения, получим.
.
Поскольку, по условию, непрерывна в , то . Тогда
.
Мы получили, что при указанных условиях, предельные переходы перестановочны.

Теорема о разрывах производной
Если функция дифференцируема на интервале ,
то ее производная не может иметь точек разрыва первого рода на этом интервале. То есть в точке производная или непрерывна, или имеет разрыв второго рода.

То есть производная дифференцируемой функции не может иметь скачков. Однако возможны точки, при стремлении к которым, предела производной не существует.
Пример:

Производная определена для всех ,   . Но в точке производная имеет разрыв второго рода, поскольку предела   не существует.

Следствие о неравенствах
Если функции и дифференцируемы при ,
и выполняются условия:
,
при .
Тогда
при .

Правило Лопиталя

См. также Решение пределов по правилу Лопиталя

Теорема о раскрытии неопределенности 0/0
Пусть функции f и g имеют производные в проколотой (двусторонней или односторонней) окрестности конечной или бесконечно удаленной () точке , причем и не равны нулю в этой окрестности. И пусть
.
Тогда, если существует конечный или бесконечный предел
,
то существует равный ему предел
.
Здесь для двусторонней окрестности. Для односторонней окрестности, , или .

Теорема о раскрытии неопределенности ∞/∞
Пусть функции f и g имеют производные в проколотой (двусторонней или односторонней) окрестности конечной или бесконечно удаленной () точке , причем не равна нулю в этой окрестности. И пусть
.
Тогда, если существует конечный или бесконечный предел
,
то существует равный ему предел
.
Здесь для двусторонней окрестности. Для односторонней окрестности, , или .

Формула Тейлора

Определения

Формула Тейлора
Пусть функция имеет в точке производную n-го порядка: . Формула

называется формулой Тейлора функции f в точке .
Многочлен Тейлора
– это многочлен
.
k-й член формулы Тейлора
– это степенная функция
Остаточный член формулы Тейлора
– это разность функции и ее многочленом Тейлора:
.

Формула Маклорена
– это формула Тейлора в точке .

Остаточный член формулы Тейлора в форме Пеано и Лагранжа

Теорема. Формула Тейлора с остаточным членом в форме Пеано
Если существует производная n-го порядка функции в точке , то
(Т1)   при .
Формула Тейлора с остаточным членом в форме Пеано
– это формула (Т1).
Теорема. Формула Тейлора с остаточным членом в форме Лагранжа
Пусть функция имеет производные до - го порядка включительно в некоторой окрестности точки :
при .
Тогда для любого существует точка , или , так что
(Т2)   .
Остаточный член формулы Тейлора в форме Лагранжа
– это функция из (Т2).

Теорема единственности

Пусть в окрестности точки имеют место следующие разложения функции f в степенные ряды:
;
.
Тогда .

Разложение элементарных функций в ряд Тейлора (Маклорена)

Далее приводится разложение элементарных функций в степенной ряд по формуле Маклорена.

;
;
,
где ;
;
;
,
где – числа Бернулли: ,   ;
;
;
;
;
;
;
;
,
;
;
.

Вычисление пределов с помощью формулы Тейлора

Одним из самых мощных методов раскрытия неопределенностей и вычисления пределов является разложение функций в степенной ряд, используя формулу Тейлора. Применение этого метода состоит из следующих шагов.
1) Приводим неопределенность к виду 0/0 при переменной x, стремящейся к нулю.
2) Раскладываем числитель и знаменатель в ряд Тейлора в окрестности точки . При этом выполняем разложение до такой степени , которая необходима для устранения неопределенности. Остальные члены включаем в .

Исследование функций с помощью производных

Возрастание и убывание функции

Монотонность на интервале

Критерий нестрогой монотонности дифференцируемой функции на интервале
Пусть функция дифференцируема на интервале .
Для того чтобы функция не строго возрастала на этом интервале, необходимо и достаточно, чтобы
при .
Для того чтобы функция не строго убывала на этом интервале, необходимо и достаточно, чтобы
при .
Достаточное условие строгого возрастания (убывания) дифференцируемой функции на интервале
Пусть функция дифференцируема на интервале .
Если при ,
то функция строго возрастает при .
Если при ,
то функция строго убывает при .

Условие только достаточное. Например, строго возрастает для всех . Но условие не выполняется, поскольку .

Монотонность на отрезке

Критерий нестрогой монотонности дифференцируемой функции на отрезке
Пусть функция непрерывна на отрезке и
дифференцируема на интервале .
Для того чтобы функция не строго возрастала на этом отрезке, необходимо и достаточно, чтобы
при .
Для того чтобы функция не строго убывала на отрезке, необходимо и достаточно, чтобы
при .
Достаточное условие строгого возрастания (убывания) дифференцируемой функции на отрезке
Пусть функция непрерывна на отрезке ,
дифференцируема на интервале .
Если при ,
то строго возрастает на отрезке .
Если при ,
то строго убывает на отрезке .

Монотонность в точке

Возрастание функции в точке
Функция строго возрастает в точке , если существует такая проколотая окрестность точки , на которой
при .
Убывание функции в точке
Функция строго убывает в точке , если существует такая проколотая окрестность точки , на которой
при .
Теорема о монотонности в точке
Пусть функция имеет производную в точке .
Если , то
функция строго возрастает в .
Если , то
функция строго убывает в .

Экстремумы

См. также Локальные экстремумы

Стационарная точка
– это точка, в которой производная равна нулю.
Критическая точка
– это точка, в которой производная функции либо равна нулю, либо не существует.
Изменение знака функции при переходе чарез точку
Пусть на некоторой проколотой окрестности точки функция определена, и
при ,
при .
То говорят, что функция меняет знак с минуса на плюс при переходе через точку .
Если
при ,
при .
То говорят, что функция меняет знак с плюса на минус при переходе через точку .
Необходимое условие экстремума
Если точка является точкой локального экстремума, то
– критическая точка. То есть либо , либо производной в не существует.
Первое достаточное условие строгого экстремума
Пусть функция дифференцируема в некоторой проколотой окрестности точки ,
и непрерывна в .
Если производная меняет знак с минуса на плюс, при переходе через точку ,
то – точка строгого минимума функции .
Если производная меняет знак с плюса на минус, при переходе через точку ,
то – точка строгого максимума функции .
Второе достаточное условие строгого экстремума
Пусть функция определена в некоторой окрестности точки .
И пусть первые производных в этой точке равны нулю, а n-я производная отлична от нуля:
.
Пусть четно.
Если ,
то – точка строгого локального минимума функции .
Если ,
то – точка строгого локального максимума функции .
Если нечетно,
то – точка не является точкой нестрогого локального экстремума функции .

Выпуклость

Выпуклость функции
Функция называется строго выпуклой вниз на открытом или закрытом интервале , если для любых точек из этого интервала и для любого выполняется неравенство
.
Функция называется строго выпуклой вверх, если при тех же условиях,
.
Функция называется нестрого выпуклой вниз, если
.
Функция называется нестрого выпуклой вверх, если
.

Геометрически это означает, что если мы проведем через любые две точки хорду, то, в случае выпуклости вниз, график функции будет ниже хорды при строгом условии, или не выше ее, при нестрогом условии. В случае выпуклости вверх, график будет располагаться выше хорды, или не ниже ее.

Критерий нестрогой выпуклости
Пусть функция дважды дифференцируема на интервале .
Функция нестрого выпукла вверх (вниз) на тогда и только тогда, когда
для всех .
Достаточные условия строгой выпуклости
Пусть функция дважды дифференцируема на интервале .
Если для всех ,
то функция строго выпукла вверх (вниз) на .
Точка перегиба
Точка называется точкой перегиба функции , если функция при переходе через эту точку меняет направление выпуклости. То есть выполняются следующие условия:
1) функция непрерывна в ,
2) фyнкция имеет в этой точке конечную или бесконечную производную ,
3) существует такая окрестность точки , на которой
функция нестрого выпукла вверх (вниз) при ,
функция нестрого выпукла вниз (вверх) при .
Критерий точки перегиба
Пусть функция непрерывна в некоторой окрестности точки ,
и дважды дифференцируема в проколотой окрестности .
Пусть существует конечная или бесконечная производная .
Точка является точкой перегиба тогда и только тогда, когда вторая производная меняет знак в этой точке. То есть
при и
при .
Либо
при и
при .
Необходимое условие наличия точки перегиба
Если – точка перегиба функции ,
и если функция имеет в некоторой окрестности точки вторую производную, непрерывную в точке , то
.
Точка распрямления графика
– это точка , в которой
.

Асимптоты

Асимптота наклонная, горизонтальная
Прямая называется асимптотой графика функции при , если
.
Если , асимптота называется наклонной. Если – горизонтальной.
Под выражением подразумевается либо , либо .
Асимптота вертикальная
Прямая называется вертикальной асимптотой графика функции , если выполняется хотя бы одно из условий:
,
.
Теорема о наклонных асимптотах
Для того чтобы прямая была асимптотой графика функции при , необходимо и достаточно,
чтобы существовали конечные пределы
,
.

Для асимптоты при , условия теоремы аналогичны.

План построения графиков функций

  1. Найти область определения функции. Выяснить, является функция четной, нечетной, периодической.
  2. Найти точки пересечения графика функции с осями координат и промежутки, на которых и .
  3. Найти асимптоты графика.
  4. Вычислить первую производную . Найти критические точки из уравнения и добавляя точки, в которых производная не существует. Найти промежутки возрастания (), убывания () и экстремумы.
  5. Вычислить вторую производную и, приравнивая ее к нулю, найти корни уравнения и точки, в которых не существует. Найти промежутки выпуклости вниз (), вверх () и точки перегиба.
  6. Если возможно, найти значения функции в экстремумах и точках перегиба.
  7. Построить график.

Использованная литература:
Я.М. Дымарский. Лекции по математическому анализу. Часть 1. Функции одной переменной. Москва, МФТИ, 2020.
Г.Е. Иванов. Лекции по математическому анализу. Часть 1. ©Иванов Г.Е., 2018.
А.Ю. Петрович. Лекции по математическому анализу. Часть 1. Введение в математический анализ. Москва, МФТИ, 2017.
А.М. Тер-Крикоров, М.И. Шабунин. Курс математического анализа. Москва, ФИЗМАТЛИТ, 2001.

Автор: Олег Одинцов.     Опубликовано:

▲
Меню