Теорема о проекциях скоростей двух точек твердого тела на прямую
Теорема
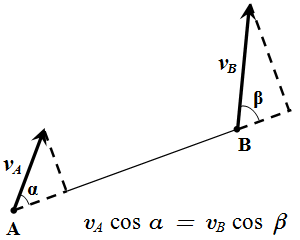
Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу.
vA cos α = vB cos β.
Доказательство

Выберем прямоугольную неподвижную систему координат Oxyz. Возьмем две произвольные точки твердого тела A и B. Пусть (xA, yA, zA) и (xB, yB, zB) – координаты этих точек. При движении твердого тела они являются функциями от времени t. Дифференцируя по времени, получаем проекции скоростей точек.
, .
Воспользуемся тем, что при движении твердого тела, расстояние |AB| между точками остается постоянным, то есть не зависит от времени t. Также постоянным является квадрат расстояния
.
Продифференцируем это уравнение по времени t, применяя правило дифференцирования сложной функции.
Сократим на 2.
(1)
Введем вектор
.
Тогда уравнение (1) можно представить в виде скалярного произведения векторов.
(2)
Выполняем преобразования.
;
(3) .
По свойству скалярного произведения
,
.
Подставляем в (3) и сокращаем на |AB|.
;
Что и требовалось доказать.
Относительная скорость
Рассмотрим движение точки B относительно точки A. Введем относительную скорость точки B относительно A.
Тогда уравнение (2) можно переписать в виде
.
То есть относительная скорость перпендикулярна вектору , проведенному из точки A в точку B. Поскольку точка B взята произвольным образом, то относительная скорость любой точки твердого тела перпендикулярна радиус вектору, проведенному из точки A. То есть относительно точки A тело совершает вращательное движение. Относительная скорость точек тела определяется по формуле для вращательного движения
.
Точку A, относительно которой рассматривают движение, часто называют полюсом.
Абсолютную скорость точки B относительно неподвижной системы координат можно записать в следующем виде:
.
Она равна сумме скорости поступательного движения произвольной точки A (полюса) и скорости вращательного движения относительно полюса A.
Пример решения задачи
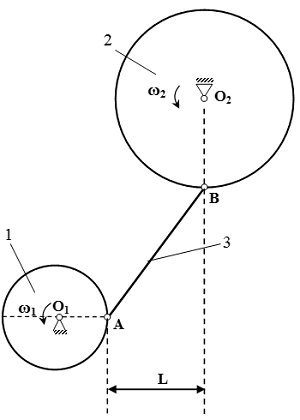
Колеса 1 и 2 с радиусами R1 = 0,15 м и R2 = 0,3 м, соответственно, соединены шарнирами со стержнем 3 длины |AB| = 0,5 м. Колесо 1 вращается с угловой скоростью ω1 = 1 рад/с. Для изображенного на рисунке положения механизма, определить угловую скорость ω2 колеса 2. Принять L = 0,3 м.
Решение задачи
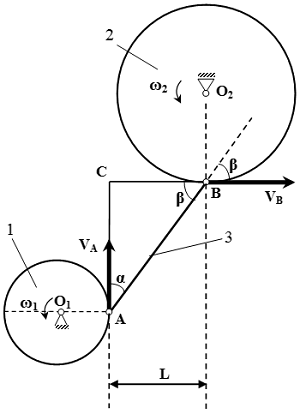
Точка A движется по окружности радиуса R1 вокруг центра вращения O1. Скорость точки A определяется по формуле
VA = ω1R1.
Вектор направлен вертикально (перпендикулярно O1A).
Точка B движется по окружности радиуса R2 вокруг центра вращения O2. Скорость точки B определяется по формуле
VB = ω2R2.
Отсюда
.
Вектор направлен горизонтально (перпендикулярно O2B).
Строим прямоугольный треугольник ABC. Применяем теорему Пифагора.
(м)
Косинус угла между вектором скорости и прямой AB, в направлении вектора , равен
.
Косинус угла между вектором скорости и прямой AB, в направлении вектора , равен
.
По теореме о проекциях скоростей двух точек твердого тела на прямую имеем:
VA cos α = VB cos β.
Отсюда
.
Находим угловую скорость колеса 2.
рад/с.
Ответ
ω2 = 0,667 рад/с
Автор: Олег Одинцов. Опубликовано:
